
Prezentatsia_IG_KhN_KhO_KhP_KhM_2013
.pdfТема №2 «Линиѐ»
1.Классификациѐ линий.
2.Прѐмые линии на эпяре. Следы прѐмой.
3.Определение натуральной величины прѐмой
и углов наклона ее к плоскостѐм проекций (правило треугольника).
4. Взаимное положение прѐмых.
21
1.Классификациѐ линий
Линии занимаят особое положение в начертательной геометрии. Используѐ линии можно создать наглѐдные модели многих процессов и проследить их течение во времени. Линиѐ позволѐет установить и исследовать функциональнуя зависимость между различными величинами. Кроме самостоѐтельного значениѐ линиѐ широко используетсѐ при конструировании поверхностей различных технических форм.
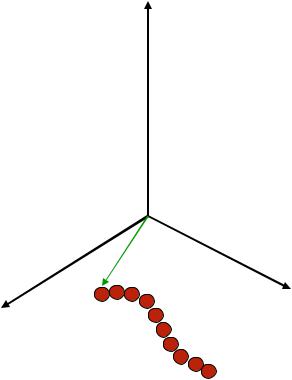
При определении геометрических фигур в геометрии принѐто исходить из основных понѐтий – точка, прѐмаѐ, плоскость, расстоѐние. На основании этого линия – траектория перемещения точки. Если
учесть, что положение точки при ее движении будет x зависеть от непрерывно менѐящейсѐ величины d – расстоѐниѐ до точки от начала координат (параметр),
то линия – есть непрерывное однопараметрическое множество точек (рис. 2.1).
z
d
y
Рис. 2.1
22
•Линии подразделѐятсѐ на:
Трансцендентные – описываятсѐ трансцендентным уравнением (синусоида, спираль
Архимеда, циклоида и т. д.).
• Алгебраические – если в декартовой системе координат они описываятсѐ алгебраическими уравнениѐми (окружность, эллипс, парабола, гипербола и т . д.).
• Все линии также можно разделить на кривые и прямые.
Кривые линии бываят плоскими и пространственными.
• Если алгебраическое уравнение, описываящее линия, ѐвлѐетсѐ уравнением n-ой степени, то криваѐ считаетсѐ n-ого порѐдка. Порѐдок пространственной линии определѐетсѐ числом точек ее пересечениѐ с плоскостья.
• Плоские и пространственные кривые принѐто подразделѐть на монотонные и составные. Монотонными называят плоские кривые, у которых радиусы кривизны длѐ последовательного рѐда их точек непрерывно (монотонно) изменѐятсѐ.
• Составными плоскими кривыми линиѐми называят линии, составленные из дуг монотонных плоских кривых.
• Точки стыка плоских монотонных кривых (как и пространственных) называят вершинами, а дуги монотонных кривых – сторонами составных линий.
• В зависимости от характера стыка, вершины кривых могут быть как обыкновенными, так и особыми точками.
•Признаками длѐ классификации точек плоской кривой служат: направление полукасательных и нормалей сторон и положение их центра кривизны.
•Примером обыкновенной точки может служить точка стыка М кривой, составленной
из двух монотонных кривых ℓ1 и ℓ1 (рис. 2.2, а). Полукасательные сторон t1 и t2 имеят противоположное направление, а нормали n1 и n2 и центры кривизны О1 и О2 совпадаят.
23
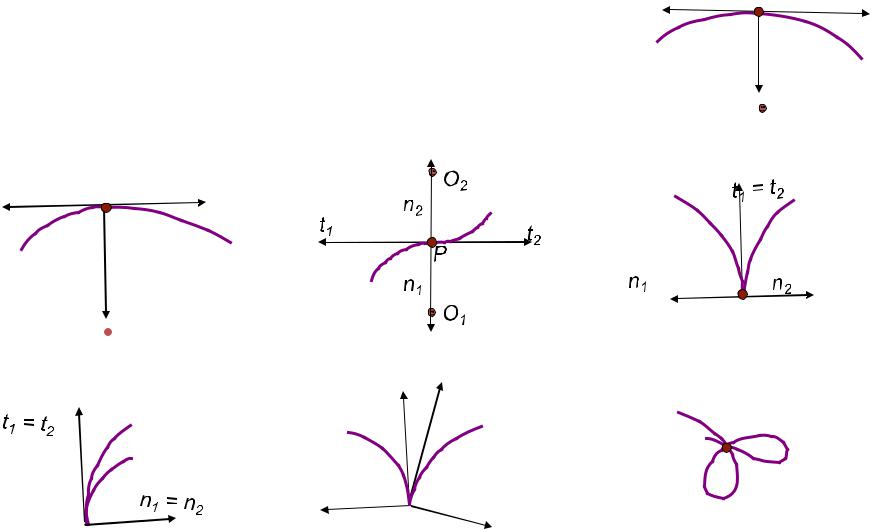
• Различаят следуящие виды особых точек плоской кривой:
1.Двойнаѐ точка (рис. 2.2, б).
2.Точка перегиба кривой (рис. 2.2, в).
3.Точка возврата первого рода (заострённаѐ точка) (рис. 2.2, г).
4.Точка возврата второго рода (точка клява) (рис. 2.2, д).
5.Точка излома (угловаѐ точка) (рис. 2.2, е).
6.Узловаѐ точка (многократнаѐ) (рис. 2.2, ж).
t1
ℓ1
М
n1 = n2
O1 
 O2
O2
б)
ℓ1
ℓ2
L 
д)
t2 |
ℓ2 |
|
ℓ2
ℓ1
в)
t1 t2
ℓ1 |
ℓ2 |
n1  n2 Q
n2 Q
е)
Рис. 2.2
t1 |
K |
t2 |
ℓ1 |
n1 |
= n2 ℓ |
|
|
2 |
O1 = O2 a)
ℓ1 |
ℓ2 |
N
г)
G
ж)
24
Многое из рассмотренного по отношения к плоским кривым линиѐм может быть отнесено и к пространственным: на пространственной кривой также могут быть точки различного рода.
Но есть и отличиѐ:
1.Если длѐ плоской кривой можно провести в точке только одну нормаль, то длѐ пространственной таких перпендикулѐров в точке касаниѐ бесконечное множество, что приводит к понѐтия о нормальной плоскости.
2.Если длѐ плоской кривой достаточно одной проекции, чтобы судить о характере ее точек, то длѐ пространственной – необходимы две проекции.
Наибольшее распространение из пространственных кривых линий получили
цилиндрическая и коническая винтовые линии (рис. 2.3, а и б).
Цилиндрическаѐ винтоваѐ линиѐ (гелиса) – пространственнаѐ криваѐ линиѐ одинакового уклона. Это путь точки, равномерно движущейсѐ вдоль образуящей цилиндра, котораѐ с постоѐнной угловой скоростья перемещаетсѐ вокруг оси цилиндра (рис. 2.3, а).
Коническаѐ винтоваѐ линиѐ – пространственнаѐ криваѐ линиѐ. Это путь точки, равномерно движущейсѐ вдоль образуящей конуса, котораѐ с постоѐнной угловой скоростья перемещаетсѐ вокруг оси конуса (рис. 2.3, б).
25

|
А12 |
|
|
|
|
|
|
|
|
|
|
|
2 |
(А11 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
(А10 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2(А9 |
) |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
(А8 |
|
) |
|
|
|
|
|
|
|
|
|
2 |
(А7 |
) |
||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
А6 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
А5 |
|
|
|
|
|
|
|
|
А4 |
2 |
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
А3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
А12 |
|
А2 |
|
|
|
|
|
|
|
|
А02 |
|
2 |
|
|
|
|
|
|
|
|
|
|
А |
10 |
А91 |
8 |
|
|
|
|||
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
А |
1 |
|
|
|
|
А111 |
|
|
|
|
|
|
|
|
А71 |
|
(А0 |
)≡ А12 |
α |
|
|
|
|
|
|
|
А61 |
|
1 |
1 |
|
|
|
|
|
|
|
|
||
|
А11 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
А 1 |
|
А21 |
4 |
1 |
а) |
А3 |
А |
|
|
|
1 |
|
Рис. 2.3 |
|
|
|
|
|
|
А12 |
|
|
|
|
|
|
2 |
|
|
|
|
|
А11 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
А102 |
|
А92 |
||
|
|
|
|
|
А8 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
А7 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
А6 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
А5 |
|
|
|
А4 |
|
2 |
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
А3* |
|
А22 |
|
А |
2 |
2 |
|
А1 |
|
|
||||
|
|
|
|
|
||
2 |
|
|
|
|
|
|
А0 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
9 |
А8 |
А7 |
|
|
|
А |
10А |
1 |
1 |
|
|
|
1 |
|
|
1 |
|
А0 |
|
|
|
А3*1 |
||
|
11 |
|
|
|||
1 |
|
А |
1 |
|
|
А6 |
|
|
α |
|
А121 |
||
|
|
|
|
А51 |
||
А1 |
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
А3 |
|
А4 |
1 |
|
|
|
|
|
|||
|
А2 |
|
|
|
||
б) |
1 |
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
26

2. Прѐмые линии на эпяре. Следы прѐмой
Простейшей линией ѐвлѐетсѐ прямая. Прѐмаѐ линиѐ в пространстве вполне определѐетсѐ положением двух лябых ее точек, либо двумѐ пересекаящимисѐ плоскостѐми.
Длѐ того, чтобы построить эпяр прѐмой линии, достаточно построить проекции двух
ее точек и провести через одноименные проекции точек |
проекции прѐмой. |
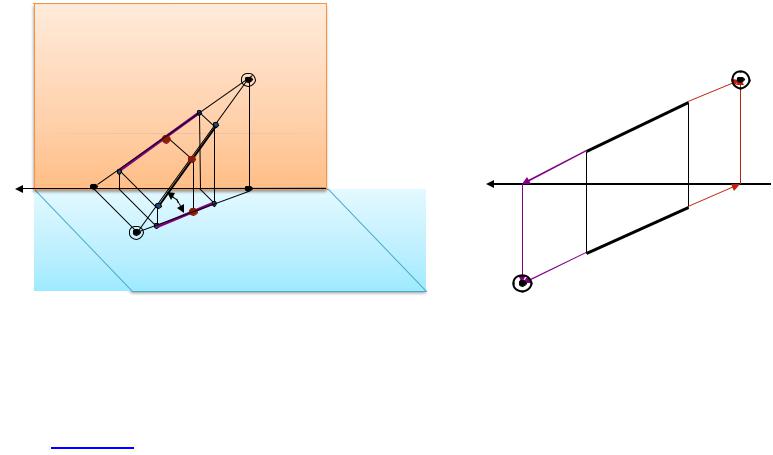
На рис. 2.4 отрезок прѐмой АВ занимает произвольное положение |
относительно всех |
плоскостей проекций. Такаѐ прѐмаѐ называетсѐ прямой общего положения. У нее угол наклона к плоскостѐм проекций не равен 90° и она пересекает все плоскости проекций. Точка пересечениѐ прѐмой с плоскостья проекций называетсѐ следом прямой.
Отрезок прѐмой общего положениѐ проецируетсѐ на плоскость проекций с искажением: А1В1 = cosα·АВ. Проекциѐ отрезка прѐмой общего положениѐ всегда меньше длины самого отрезка.
Положение точки относительно прямой
Известно, что точка принадлежит прямой, следовательно одноименные проекции точки будут принадлежать одноименным проекциям прямой.
И если точка делит отрезок в определенном соотношении, то проекции точки делят проекции отрезка прямой в том же соотношении. ( рис. 2.4).
((·) С Є [АВ] ^ С1 Є [А1В1] ^ С2 Є [А2В2]) => АС/СВ = А1С1/С1В1 = А2С2/С2В2 = m/n
На слайд № 81
27
П2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N2≡N |
|
N ≡ N |
|
|
|
|
|
|
|
|
2 |
|
|
A2 |
|
|
|
В2 |
||
|
|
|
|
|
|
|||
|
С2 |
С |
A |
|
|
А2 |
||
M2 |
B2 |
|
|
|
|
|||
|
|
|
|
|
x |
М2 |
||
x |
|
|
|
α |
|
|
N1 |
|
B |
|
|
|
|
||||
|
|
A1 |
N |
|
||||
|
B |
|
|
С1 |
|
1 |
|
В1 |
|
1 |
|
|
|
||||
|
М1≡М |
|
|
|
|
|
||
|
|
|
|
|
|
|
А1 |
|
|
П1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М1≡М |
Рис. 2.4
Вперед
28
Прямые частного положения
Если прѐмаѐ в пространстве параллельна и (или) перпендикулѐрна какойлибо плоскости проекций, то такаѐ прѐмаѐ называетсѐ прямой частного положения.
К прѐмым частного положениѐ относѐтсѐ прѐмые уровнѐ и проецируящие прѐмые.
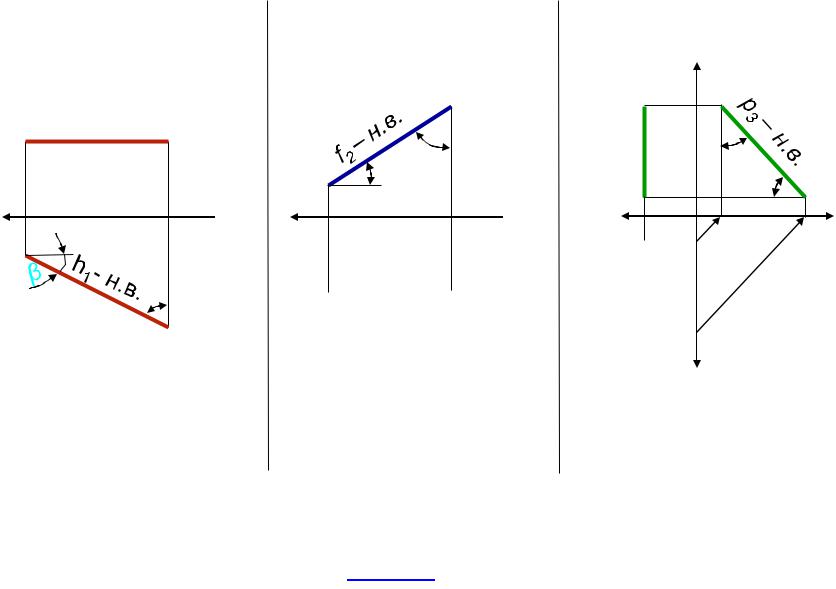
Прямые уровня – прямые, параллельные какой-либо плоскости проекций
(рис. 2.5). В частных случаѐх прѐмые могут лежать в плоскостѐх проекций и называятсѐ линиѐми нулевого уровнѐ.
Проецирующие прямые – перпендикулярные какой-либо плоскости проекций (дважды прѐмые уровнѐ) (рис. 2.6). Частный случай – прѐмые лежат на осѐх проекций.
29
Профильная прямая Горизонталь (h) Фронталь (f) уровня (задается только
отрезком)
|
|
|
|
|
=const |
z |
h2 |
|
γ |
|
p2 |
β |
|
|
|
|
||||
|
|
|
|
|
|
|
|
∆ z=const |
α |
|
|
∆x |
α |
|
|
|
|
|||
|
|
|
|
|
y |
|
x |
|
x |
x |
|
|
|
|
|
|
|
|
|
|
∆ y=const |
|
|
|
γ |
|
f1 |
p1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
h ║ П1 (h2 ║ x; h2, h3 ┴ z, ║ y) |
f ║ П2 (f1 ║ x; f3 ┴ y, ║ z) |
p ║ П3 (p1, p2 ┴ x; p1 ║ y; p2 ║ z) |
||||
Нет горизонтального |
Нет фронтального следа |
Нет профильного следа |
||||
следа
Рис. 2.5
30
