Концепции современного естествознания

принципами, часто противоположными принятым ранее; новыми подходами; новыми понятиями, как частными, применяемыми в отдельных областях познания, так и общенаучными.

7.Наука находится в процессе перманентного развития.

8.Область научного исследования постоянно расширяется, распространяясь на объекты, которые до этого находились вне сферы ее интересов.

9.Существуют три механизма эволюции: диссипативные структуры в неживом мире, естественный отбор в живой природе, культура в человеческом обществе.

10.Наука развивается в пределах чувственного и логичного и ограничена возможностями наших чувств и законами мышления. Особенности органов чувств и мышления, как и эволюция, являются ее граничными условиями. Наука как бы находится в треугольнике, ограниченном возможностями человека и творчеством природы. Она постоянно расширяет свои границы, оставаясь принципиально ограниченной.

11.В настоящее время наука столкнулась с четвертым ограничением – экологическим. Ее развитие может привести к уничтожению биосферы и

еесамой. Наука может это сделать, но не способна создать равноценный искусственный мир. Разрушать всегда легче, чем созидать – и для отдельного человека и для человечества в целом.

12.Наука создает информацию о мире, и это должно иметь смысл. Люди сами находятся в цепи жизни и ответственные за нее перед нею и собой.

81

Глава 2. Математика как универсальный язык и орудие естествознания

Природа говорит языком математики; буквы этого языка – круги, треугольники и иные математические фигуры.

Г. Галилей

Зрелость науки обычно измеряется тем в какой мере она использует математику.

И. Кант

2.1. Предмет и специфика математики

Математика – это большой город, чьи предместья не перестают разрастаться, в то время как центр периодически перестраивается, следуя каждый раз все более ясному плану и стремясь все к более и более величественному расположению, в то время как… старые кварталы с их лабиринтом переулков сносятся для того, чтобы проложить к окраине улицы все более прямые, все более широкие и удобные…

Никола Бурбаки

При анализе специфики естествознания и гуманитаристики мы обращались к двум важнейшим аспектам семиотики – семантическому и прагматическому. У семиотики есть еще и третья сторона, синтаксическая. Синтактика (от греч. syntaxis – составление) изучает сочетание знаков, правила их образования и преобразования безотносительно к какимлибо семантическим и прагматическим функциям. Подлинным триумфом синтаксического подхода является математика, царство символьных записей, формул, теорем, многозвенных преобразований, доказательств. Математика имеет для естествознания непреходящее значение.

Математика – наука о количественных отношениях и пространственных формах действительного мира. Приложения математики разнообразны. Принципиально область применения математического метода не ограничена: все виды движения материи могут изучаться математически. Однако роль и значение математического метода в различных случаях различна. Важнейшим условием возникновения и существования точного естествознания является использование научного эксперимента, а также математического аппарата исследований [14].

Самое лаконичное определение математики дает Никола Бурбаки (коллективное имя группы французских математиков). Он определяет со-

82

временную математику как науку о структурах, «единственными математическими объектами становятся, собственно говоря, математические структуры».

У американского физика лауреата Нобелевской премии Евгения Вигнера есть работа под названием «Непостижимая эффективность математики в естественных науках». Достаточно шутливое определение математики, данное здесь Вигнером, звучит так: «Наука о хитроумных операциях, производимых по специально разработанным правилам над специально придуманными понятиями».

Восхищаясь блестящими примерами успехов этой науки, Вигнер пишет: «Математический язык удивительно хорошо приспособлен для формулировки физических законов. Это чудесный дар, которого мы не понимаем и которого не заслуживаем. Нам остается лишь благодарить за него судьбу и надеяться, что и в своих будущих исследованиях мы сможем по-прежнему пользоваться им. Мы думаем, что сфера его применимости (хорошо это или плохо) будет непрерывно возрастать, принося нам не только радость, но и новые головоломные проблемы» [15].

Но, говоря о важности применения математики в естествознании, мы не должны абсолютизировать ее роль. Математические формулы сами по себе абстрактны и лишены конкретного содержания. Математика является лишь орудием, или средством, физического исследования, но и экономика и лингвистика и т.п., согласованные с научным наблюдением и экспериментом, физические исследования наполняют математические формулы конкретным содержанием.

Ученые часто говорят о красоте математических уравнений. Хотя красота – понятие туманное, но она часто служит источником вдохновения. Однажды в беседе с А. Эйнштейном немецкий физик В. Гейзенберг заметил: если природа приводит нас к математическим выражениям необычайно простым и красивым, то мы невольно воспринимаем их как истинные. Еще дальше в этом отношении пошел английский математик и физик П. Дирак, который провозгласил: «Красота уравнений важнее, чем их согласие с экспериментом». Это не означает принижения эксперимента, а значит только то, что красота и истинность совпадают в простоте и общности математических выражений. Физик нередко изучает такие явления природы, которые вначале кажутся чрезмерно сложными и запутанными, даже случайными. Но при использовании надлежащего математического аппарата сложное физическое явление может свестись к очень простой формуле.

Американский ученый Гамов (русский по происхождению) рассказывает, что среди физиков и математиков Геттингена была очень популярна такая задачка: как записать все числа от 1 до 100, используя только циф-

83

ру 2 и все возможные алгебраические действия. Причем двойку можно было употреблять только четыре раза.

Например: 1 = 2 · 2/2 · 2, 2 = 2/2+2/2,

. . . . . . .

5 = 22+2/2 и т. д.

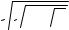
Когда Дирака познакомили с условием этой задачи, он очень быстро нашел общее решение, то есть показал, как можно записать любое число N, причем используя цифру 2 только три раза . Вот это решение:

N = – log2 log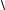2 .... 2

где число корней равно N. Можно проверить вывод Дирака и оценить элегантность его математических способностей.

Связь между симметрией пространства и законами сохранения установила немецкий математик Эмми Нётер (1882 – 1935). Она сформулировала и доказала фундаментальную теорему математической физики, названную ее именем, из которой следует что из однородности пространства и времени вытекают законы сохранения соответственно импульса и энергии, и из изотропности пространства – закон сохранения момента импульса.

Выявление различных симметрий в природе, а иногда и постулирование их стало одним из методов теоретического исследования микро-, макро-, мезо- и мегамира. Возросла в связи с этим роль весьма сложного и абстрактного математического аппарата – теории групп – наиболее адекватного и точного языка для описания симметрии. Теория групп – одно из основных направлений современной математики. Значительный вклад в ее развитие внес французский математик Эварист Галуа (1811 – 1832), жизнь которого рано оборвалась: в возрасте 20 лет он был убит на дуэли.

С помощью теории групп русский минеролог и кристаллограф Е.С. Федоров (1853 – 1919 гг.) решил задачу классификации правильных пространственных систем точек – одну из основных задач кристаллографии. Это исторически первый случай применения теории групп непосредственно в естествознании.

Существенное ограничение об однородном и изотропном пространственном распределении материи во Вселенной, налагаемое на уравнения общей теории материи и составляющее основу космологического принципа, позволило А.А. Фридману (1888 – 1925 гг.) предсказать расширение Вселенной.

Анализируя роль принципов инвариантности современный американский физик-теоретик Э. Вигнер, лауреат Нобелевской премии 1963 г., показавший эффективность применения теории групп в квантовой меха-

84

нике, выделил ряд ступеней в познании, поднимаясь на которые мы глубже и дальше обозреваем природу, лучше ее понимаем. Вначале в хаосе повседневных фактов человек замечает некоторые эмпирические закономерности. Затем, выделяя общие свойства природных явлений и анализируя их связи, он формулирует математические законы природы, учитывая при этом начальные условия, которые могут иметь любой, даже случайный характер. Например, в классической механике в качестве начальных условий могут выступать координаты и скорость тела в некоторый начальный момент времени. Наконец, синтезируя уже известные законы, находят ряд принципов, позволяющих дедуктивным путем определить уже известные и пока неизвестные утверждения, предсказывающие те или иные физические явления и процессы.

Функция, которую несут принципы симметрии, по утверждению Э. Вигнера, состоит в наделении структурой законов природы или установлении между ними внутренней связи, так как законы природы устанавливают структуру или взаимосвязь в мире явлений. Так создаются теории, охватывающие широкий круг физических явлений и процессов. Следующая ступень – анализ самих принципов границ или условий и выявление тех, при которых они выполняются. Идею выявления основополагающих принципов и их последовательное применение при

описа-нии и объяснении природных явлений впервые предложил и реализовал с применением математического аппарата Исаак Ньютон еще в начале развития классической физики и задолго до появления современных представлений об инвариантности и симметрии. В своем труде «Оптика» он писал: «Вывести из явлений два или три общих принципа движения и затем изложить, как из этих ясных принципов вытекают свойства и действия всех вещественных предметов, вот что было бы очень большим шагом в философии, хотя причины этих принципов и не были еще открыты». По своему содержанию и месту в теории познания такие принципы носят аксиоматический характер.

Если на ранних стадиях развития естествознания математика была нужна ученым для обеспечения количественной точности и объективной достоверности результатов исследования, то в эпоху бурного развития естествознания в конце XIX – в начале ХХ века математика стала служить средством получения простых (изящных, красивых) законов о сложных

85

явлениях природы.

К числу сведений, восходящих к весьма отдаленному прошлому, относятся, очевидно, и необъяснимо высокие познания древних в области математики, тоже не являвшиеся результатом их практической деятельности, которая была бы известна нам. Понятие «миллион», отмечает Р. Керам, было принято в европейской математике только в XIX веке. Но оно было известно древним египтянам, имевшим даже специальный знак для его обозначения.

Число π известно в истории математики как «число Лудольфа» – голландского ученого XVII века, рассчитавшего соотношение длины окружности к ее диаметру. Однако в Москве в Музее изобразительных искусств имени Пушкина хранится египетский папирус, из которого явствует, что египтянам давно было известно число π.

Но оказывается, еще до египтян число это было известно в Шумере. Знали в Шумере и теорему, которую тысячу лет спустя открыл Пифагор. Ученые, жрецы и хранители знаний Древнего Шумера решали сложные алгебраические задачи, квадратные уравнения с несколькими неизвестными, задачи на сложные проценты и даже задачи, выходившие за пределы алгебры. Они предавались этим занятиям среди окружавшей дикости и варварства их эпохи. Писали они деревянными палочками на влажной глине, и то, что они делали, надолго опережало как практические потребности жизни, так и общий уровень знаний. Мы снова видим высокие познания, появляющиеся как бы внезапно и на уровень которых человечество выходит только тысячелетия спустя. Достаточно сказать, что среди клинописных текстов, найденных в Шумере, содержится математический ряд, конечный итог которого выражается числом 195 955 200 000 000. Это было число, которым, по мнению специалистов, европейская наука не умела оперировать даже во времена Декарта и Лейбница.

AD HOS (лат.) – кстати

Цифры роковые и счастливые. В большинстве стран мира цифра «13» считается числом, приносящим несчастье. Эта точка зрения появилась еще в глубокой древности, когда люди начали постигать основы математических знаний. Число «13» было «неудобным» для использования, так как не делилось ни на какую другую цифру, кроме как на самое себя.

ВЯпонии и Китае считают, что несчастья приносят цифры 19, 33 и 42.

Вдревние времена на Ближнем Востоке, а позднее в Древнем Египте и Риме, число семь считалось священным. Ему придавалось магическое и

даже символическое значение. Так, Вавилонская башня имела семь этажей. Рим, был построен на семи холмах. Древние евреи также считали семерку священной цифрой. По индийской религии, мир создан семью си-

86

лами. Будда сидит под священной смоковницей с семью плодами. Китай и Япония также почитали цифру семь. В Древней Греции было известно о семи чудесах света и семи знаменитых мудрецах. В Библии говорится о сотворении мира за семь дней, о семи смертных грехах и семи голодных годах. Не будем забывать, что неделя состоит из семи дней, радуга

имеет семь цветов, а в октаве – семь нот…

С развитием в ХХ столетии квантовой и волновой механики, физики фундаментальных частиц высоких энергий наука столкнулась с принципиально ненаглядными и противоречивыми явлениями микромира.

Так, фундаментальные частицы обладают одновременно свойствами частицы и волны, и такие микрообъекты изобразить в виде наглядных моделей в принципе невозможно, но они поддаются описанию соответствующими математическими уравнениями.

Но дело не ограничивается математическим описанием объекта: дальше нужно производить преобразования объекта, чтобы исследовать его. Так вот, если найдена адекватная физическим идеям математическая формула, то дальше мы можем преобразовать не сам физический объект, а замещающую его формулу по правилам математики. Затем результаты математических преобразований проверяют в физическом эксперименте, который зачастую соответствует математическим преобразованиям.

Таким образом, если физический объект правильно выражен формулой и если правила математических преобразований согласованы с изучаемыми физическими процессами, то физические преобразования объектов могут быть заменены математическими преобразованиями исходных формул. В таком случае результаты математических преобразований будут как бы автоматически соответствовать физическим экспериментам, то есть математика выполняет в естествознании эвристическую, или познавательную, роль.

Именно в этой связи доказательство новой теоремы или построение ранее неизвестного конструкта расценивается как математический успех. Показательны в этом отношении страсти вокруг теоремы Ферма.

Надо полагать, что мы хорошо знакомы с уравнением х2 + у2 = z2 , которому удовлетворяют многие тройки целых чисел, например х = 3, у = 4, z = 5. Французский математик Пьер Ферма утверждал, что уравнение хn + уn = zn (где n – целое число, больше 2) не имеет решений в целых положительных числах. На доказательство теоремы Ферма некоторыми математиками затрачены значительные усилия. Почему теорема занимает мысли математиков? Потому что новые сведения о ней расширят их представление о характере упорядоченности целых положительных чисел.

Примеры относительно натуральных чисел и теоремы Ферма достаточно просты. Разумеется, абсолютное большинство математиков зани-

87

мается проблемами поважнее теоремы Ферма. Это обстоятельство не меняет сути дела: интерес математика заключен в изобретении многообразий упорядоченных математических конструктов.

Если многообразие математических конструктов не упорядочено, т.е. невозможно их сопоставление друг с другом, то работа математика теряет всякий смысл. Дабы этого не случилось, математик внимательно следит за тем, чтобы математическая теория была непротиворечивой. Математическая теория называется непротиворечивой, если в ней не наличествуют два или больше взаимно исключающих предложения. Наличие противоречий «разваливает» математическую теорию. Простой пример: если бы согласно таблице умножения 3 · 3 = 9 и 3 · 3 = 8, то ее невозможно было бы продуктивно использовать.

AD NOTAM (лат.) – к сведению Какое число самое большое?

Корректно ответить на этот вопрос нельзя, поскольку числовой ряд не имеет верхнего предела, а значит, теоретически запись числа на бумаге или экране компьютера может состоять из бесконечного ряда цифр. Однако среди чисел, имеющих собственное имя, а таковых, как ни странно, не так уж много, есть свой рекордсмен. Это буддийское число асанкхейя, которым исчисляется количество космических циклов, необходимых для обретения нирваны. Дословно оно переводится как неисчислимое, однако имеет определенное значение, равное 10140 (то есть единица со 140 нулями). На втором месте стоит число гугол (10100 – единица и сто нулей), которое в 1938 году решил ввести в обиход американский математик Эдвард Каснер, а автором непереводимого названия стал 9-летний племянник ученого. Интересно, что если всем остальным числам с «именами» можно подобрать соответствующее число объектов (например, количество звезд в видимой части Вселенной оценивается в 70 секстильонов – 7 · 1022, а количество атомов, из которых состоит земной шар имеет порядок додекальонов), то гугол и тем более асанкхейя абсолютно «виртуальны». Дело в том, что число электронов во Вселенной (а большего числа реальных объектов просто не существует), согласно некоторым теориям, не превышает 1087, что в 10 триллионов раз меньше гугола.

88

рии. В том, что еще вчера считалось непротиворечивым, подтверждаемым и эффективным, уже сегодня могут быть обнаружены элементы противоречивости, неподтверждения, неэффективности. Если это случается, то приходится пересматривать статус теории, принимать меры к тому, чтобы в той или иной форме избавиться от выявленных нежелательных симптомов ненаучности. Сказанное в полной мере относится к математике.

Подобно другим ученым, математики стремятся в области своей компетенции к максимальному успеху. То и дело встречаясь с нарушениями критерия непротиворечивости (особенно это связано с открытием различного рода парадоксов).

Английский философ и логик Б. Рассел предложил следующий популярный вариант открытого им парадокса математической теории множеств.

Представим, что совет одной деревни так определил обязанности парикмахера этой деревни: брить всех мужчин деревни, которые не бреются сами, и только этих мужчин. Должен ли он брить самого себя? Если да, то он будет относиться к тем, кто бреется сам, а тех, кто бреется сам, он не должен брить. Если нет, он будет принадлежать к тем, кто не бреется сам, и, значит, он должен будет брить себя. Мы приходим, таким образом, к заключению, что этот парикмахер бреет себя в том и только в том случае, когда он не бреет себя. Это, разумеется, невозможно. Рассуждение о парикмахере опирается на допущение, что такой парикмахер существует. Полученное противоречие означает, что это допущение ложно и нет такого жителя деревни, который брил бы всех тех и только тех ее жителей, которые не бреются сами.

Обязанности парикмахера не кажутся на первый взгляд противоречивыми, поэтому вывод, что его не может быть, звучит несколько неожиданно. Но этот вывод не является все-таки парадоксальным. Условие, которому должен удовлетворять деревенский брадобрей, на самом деле внутренне противоречиво и, следовательно, невыполнимо. Подобного парикмахера не может быть в деревне по той же причине, по какой в ней нет человека, который был бы старше самого себя или который родился бы до своего рождения. Рассуждение о парикмахере может быть названо псевдопарадоксом.

Некоторые математики, среди них выдающийся немецкий ученый Д. Гильберт, отважились на попытку доказательства непротиворечивости математики в тех случаях, когда она представлена в виде аксиоматически формальной системы. Многие надеялись на успех этой программы. Но в 1931 г. выдающемуся австрийскому математику К. Геделю удалось доказать теорему, которая вызвала в научном мире что-то вроде шока. Гедель

90