1.4.3. Метод случайного поиска

В данном методе возможные направления определяются с помощью генератора псевдослучайных чисел с равномерным распределением в диапазоне -1,…,1.

Д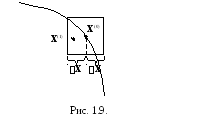ля этого в исходной точке Х⁽⁰⁾ рассматривается куб с гранью 2x (рис.1.9) и считается значение функции F₀. Случайным образом выбирается точка в кубе , где_i – псевдослучайное число (-1  _i  1). В точке Х⁽¹⁾ считается значение функции F₁.

Если F₁ < F₀, то исходная точка Х^(0)­­­ переносится в точку Х⁽¹⁾ и процедура повторяется. Если F₁ > F₀, то выбранная точка Х⁽¹⁾ считается неудачной, и вместо нее отыскивается новая точка. Вдали от минимума вероятность попадания в область возможных направлений близка к 50%. По мере приближения к решению величина x уменьшается.

Достоинства метода: простота алгоритма, не требующего вычисления производных. Недостаток - большое число итераций.

1.4.4. Метод деформированного многогранника

Метод основан на вычислении целевой функции в (n+1) точках Х₁, Х₂, Х₃ (рис.1.10).Среди них ищется точка сF_MAX (в нашем случае Х₂ c F₂). Затем найденная точка проектируется через центр тяжести остальных точек (Х₁ и Х₃) с коэффициентом  (0    1) и получается новая точка (Х₄). В полученной точке считается F (здесь F₄). С полученными тремя точками (Х₁, Х₃, Х₄) проводим аналогичные операции – проводится дальнейшая деформация.

Метод деформированного многогранника и случайного поиска относят к методам нулевого порядка, поскольку они не требуют вычисления производных и строятся только на вычислении значений целевой функции.

1.5. Оптимизация с учетом ограничений в форме равенств

Рассмотрим общую задачу нелинейного программирования

F(X)  min при G(X) = 0.

Здесь X = {x₁,…,x_n} – вектор неизвестных,

G(X) = {g₁(X),…,g_m(X)}- вектор-функция ограничений в форме равенств.

Соотношение m и n определяет возможности решения. Если m > n, то система ограничений несовместна и решения нет. Если m = n, то может существовать единственное решение. При m < n система ограничений имеет множество решений, среди которых и надо найти оптимальное.

Рассмотрим основные методы оптимизации при ограничениях – равенствах.

1.5.1. Метод прямой оптимизации

Данный метод используется, когда G(X) представлена простыми функциями, например линейными. В этом случае m неизвестных из n можно аналитически выразить через остальные k = n – m и подставить эти выражения в F(X). Тогда получим новую функцию,

условие минимума которой будет иметь k уравнений:

.

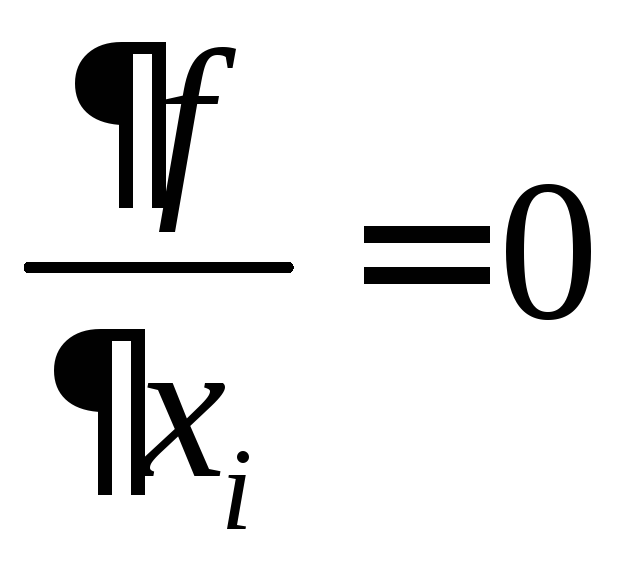Решение этих уравнений позволяет найти все k составляющих вектора . Остальные переменные находятся подстановкой в ранее найденные выражения.

Рассмотрим пример:

F(X) = 5 + x₁² + x₂²  min;

g(X) = x₁ + x₂ – 2 = 0;

 = x₂

x₁ = 2 – x₂

f() = f(x₂) = 5 + (2 – x₂)² + x₂²  min,

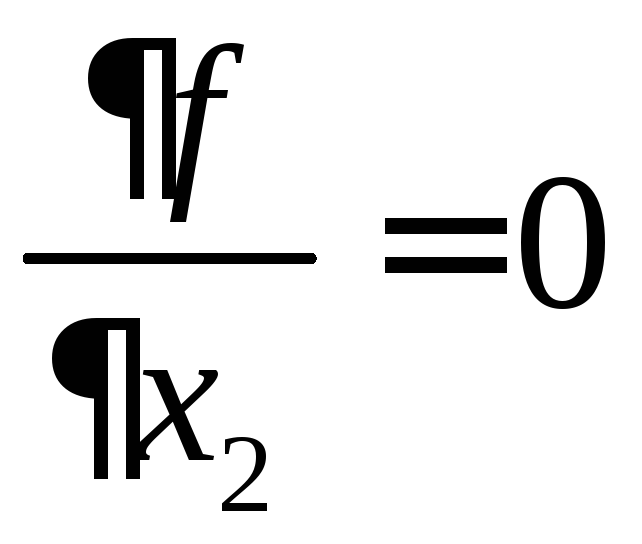, –2(2 – x₂) + 2x₂=0, x₂ = 1;

x₁ = 2 – 1 = 1.

Метод прямой оптимизации прост, но может быть использован для решения только аналитически заданных функций сравнительно простого вида.

1.5.2. Метод приведенного градиента

Здесь исходный вектор неизвестных делится на два блока

X ={, Y}, где  – свободные, в количестве k, а Y – зависимые, в количестве m.

При этом зависимость Y() безусловно существует, но в неявной форме, то есть не определяется аналитическим выражением.

Выражение для градиента целевой функции можно записать по правилу вычисления производной с учетом неявных функций.

,

где в скобках указаны производные, взятые с учетом только явной зависимости.

Производную можно определить аналогично из условияG(X)=0.

Поскольку G(X) = G(,Y) = 0, то .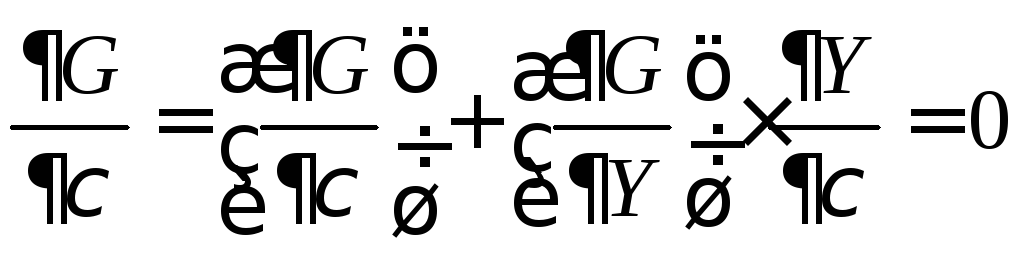

Откуда

и ,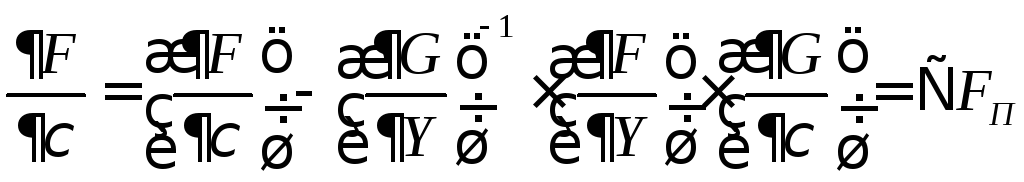

где – приведенный градиент.

Приведенный градиент может использоваться в процедуре градиентного метода.

Изобразим на графике процесс поиска решения методом приведенного градиента в пространстве 2-х переменных (рис.1.11).

З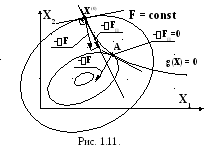десь– это проекция антиградиента на линию ограничений, в общем случае – на плоскость.

Решение лежит в точке A, где линия ограничения касается ближайшей линии F = const.

Сложности метода связаны с определением проекции, для чего требуется обращение матрицы , имеющей размерностьmm.