1.3. Особенности задачи нелинейного программирования

По сравнению с линейными задачи нелинейного программирования имеют ряд особенностей:

1. Допустимая область может быть не выпуклой (рис.1.2);

Рис. 1.2.

2. Решение может лежать как внутри допустимой области, так и на границе;

3. Целевая функция может иметь несколько экстремумов, один из них является глобальным, остальные – локальными (рис. 1.3)

Рис. 1.3.

Все это осложняет решение, поэтому, в отличие от линейного программирования, здесь существует множество методов решения подобных задач.

Ниже будут рассмотрены основные методы нелинейного программирования. Для иллюстрации их будет использована F(Х) при n=2 и представляемая на графике в виде линий F = const (рис.1.4).

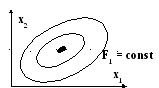
Рис. 1.4.

1.4. Методы безусловной оптимизации

Пусть задана целевая функция F(Х)min без ограничений, где Х={x₁,…,x_n}.

Если F(x) задана аналитически, то условие экстремума

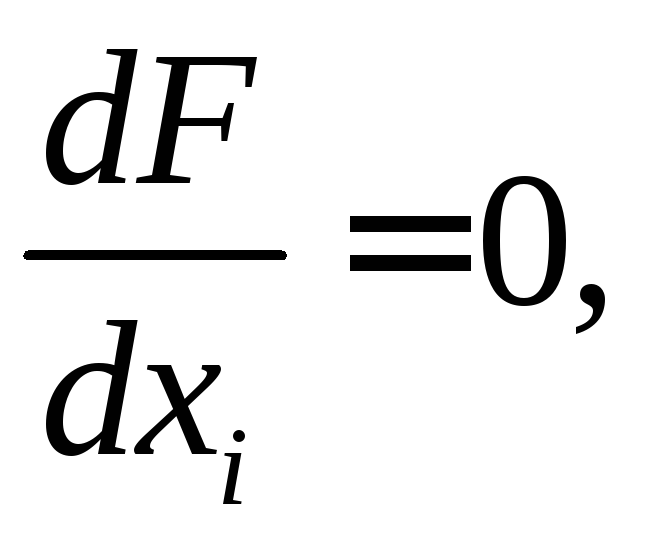гдеi= 1,…,n.

Как известно, условие минимума: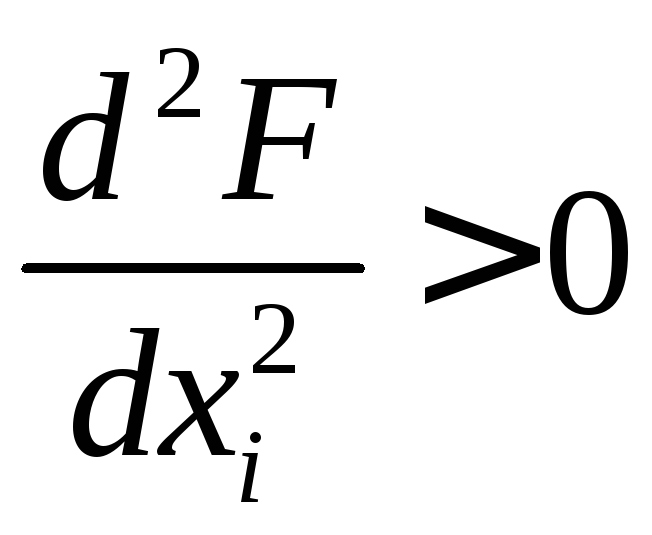

Далее будем рассматривать численные методы решения, которые удобны для реализации на ЭВМ. На сегодняшний день большинство таких методов относятся к методам возможных направлений (рис.1.5).

Расчет начинается с исходного приближенияx₀. В точке x₀ рассматривается несколько направлений . Направления, ведущие к снижению F (здесь 1 и 3) называют возможными направлениями (ВН).

По любому из этих возможных направлений осуществляется переход в следующую точку: , гдеt – шаг.

Получаем общее уравнение: ,

где k – номер итерации (шага).

Величина шага t определяет сходимость процесса:

• если t0, то сходимость медленная, но надежная;

• если t – большой, то сходимость быстрая, но процесс может расходиться.

Наилучшая сходимость обеспечивается выбором t_ОПТ по критерию F(Х)min на выбранном направлении . Оптимальный шаг можно выбрать, еслиF(x) представить по возможности как

и по условию минимума

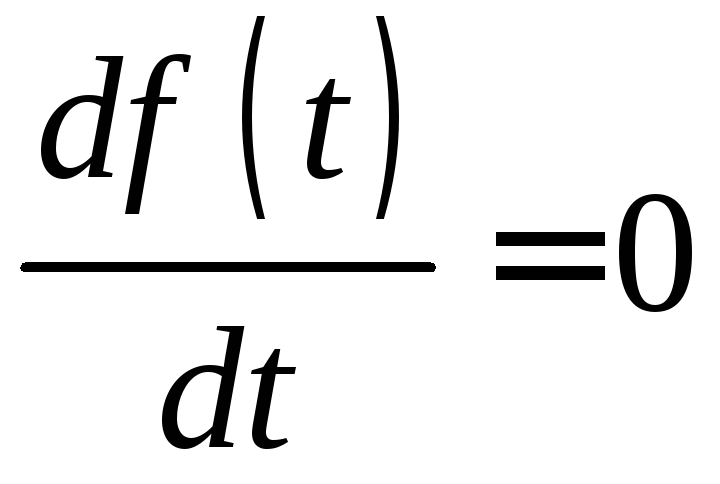найти оптимальный шаг .

Чаще f(t) аппроксимируют кривой второго порядка:

Для определения параметров a,b и c считают f в трех точках:

- при t = 0, когда x = x₀ (F(x₀) = F₀);

- при t = 1, (F(x₁) = F₁);

- при t = 2, (F(x₂) = F₂).

После этого составляют систему уравнений,

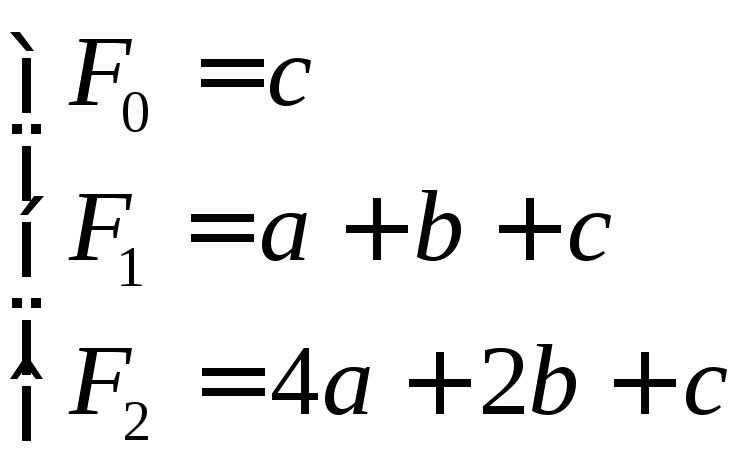
из решения которой находят a,b и c.

Из условия минимума функции

определяют оптимальный шаг

,

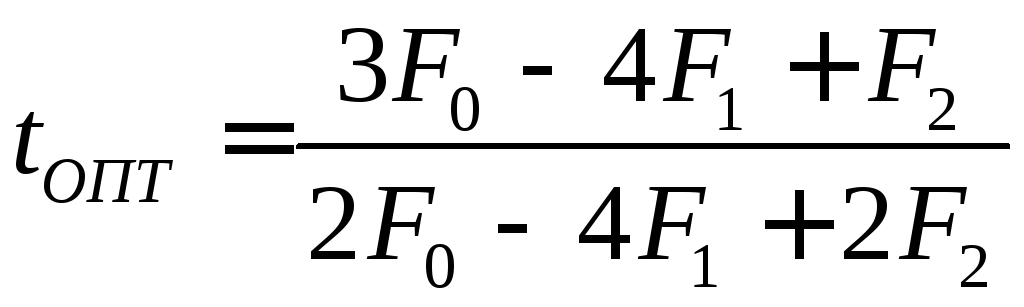
Методы, в которых определяется t_ОПТ, называются методами скорейшего поиска. Эти методы широко используются при решении задач.

В зависимости от выбора возможных направлений различают несколько методов.

1.4.1. Метод покоординатного спуска

Здесь возможные направления определяются по ортам e_i (единичным векторам по осям координат). Каждая переменная x_i последовательно (рис.1.6) оптимизируется, начиная с x₁.

Оптимизация может проводиться различными методами, применимыми только для функций одной переменной.

После нахождения оптимизацию проводят по второй переменной (x₂) и т.д.

Аналогично проводятся последующие циклы и весь процесс.

Достоинства метода: простота. Недостатки: плохая сходимость для функций типа “овраг”.

1.4.2. Градиентный метод

Возможное направление выбирают противоположным градиенту:

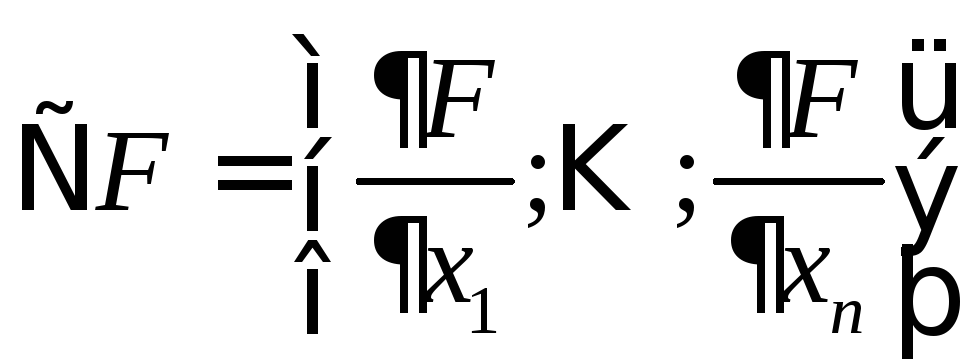
Основное уравнение:

.

Составляющие градиентанаходятся через конечные приращения (рис.1.7):

.

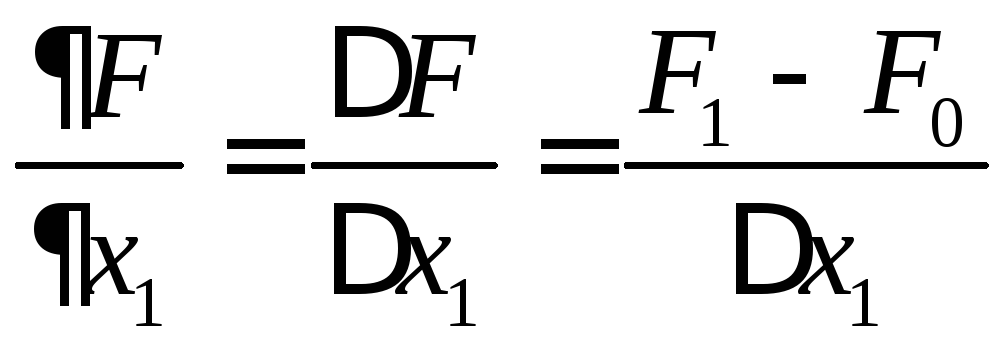Так как tg  tg, то этот метод имеет погрешность в определении градиента, которая зависит от величины приращения аргумента.

Для снижения погрешности используют метод центрированных приращений.

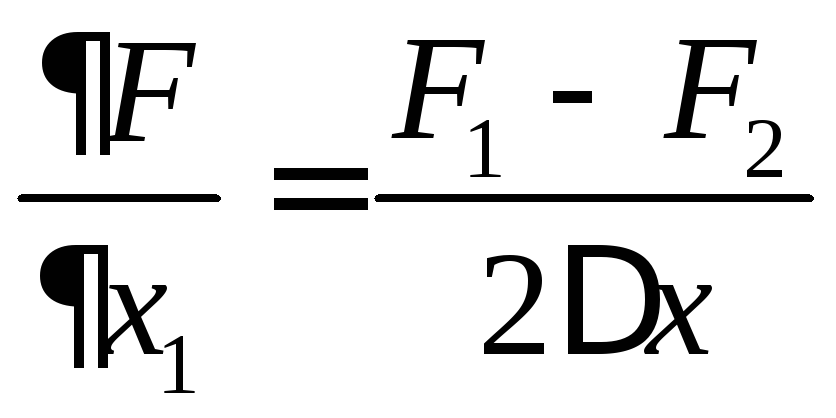
Градиентный метод часто сочетается с выбором оптимального шага. Для выбора используется пробный шаг t_0, в конце которого определяются координаты Х1 и составляющие градиента. По значениям градиента в точках Х и Х1 определяется шаг близкий к оптимальному. Алгоритм метода приведена рис.1.8.:

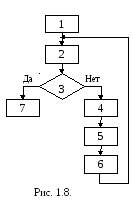
1. Исходное приближение Х = Х⁽⁰⁾;

2. Определение градиента F |_X;

3. Сравнение |F| < eps;

4. t₀ и определение ;

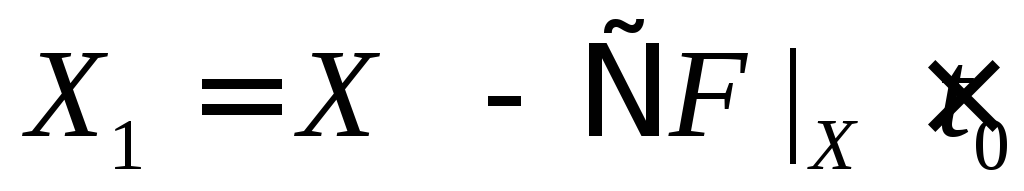5. Определение t_ОПТ;

6. Определение ;

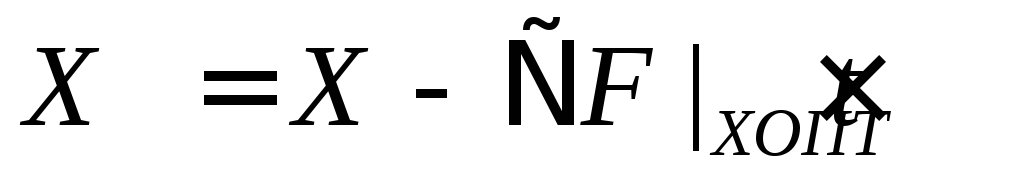7. Выход.

Метод широко используется в программах оптимизации режимов.