Пособие 09

(другие названия - F -критерий, статистика Фишера) представляется собой оценку соотношения

s 2 F 1 ,

s22

где s12 , s22 - выборочные дисперсии, которые оцениваются, как определенные для одной и той же генеральной совокупности. F -статистика проверяет гипотезу

H0 : 12 22 2 ,

т.е. гипотезу о том, что обе выборки являются выборками из одной и той же генеральной совокупности, против альтернативной гипотезы.

При оценки качества модели регрессии F -статистика используется в качестве вспомогательного инструмента. Для модели регрессии F -критерий

оценивается как соотношение объясненной части регрессии sфакт2 и остаточной части регрессии sост2

sфакт2

F sост2 ,

^_ 2

( Yt Y )

^2

( Yt Yt )

n - объем выборки, m - число объясняющих переменных в уравнении регрессии. Схема дисперсионного анализа представлена в Таблице П.1

Таблица П.1

Таким образом, F -статистика множественной регрессии определяется

91

и F -статистика парной модели

( Y t Y )2

критерия выше некого критического значения Fкритич , то считают, что обе рассматриваемые выборки принадлежат одной генеральной совокупности.

92

Приложение 2

Статистические таблицы

Значение t , N -статистики Стьюдента

93

94

95

Приложение 3

Распределение Стьюдента

В отличии от стандартного нормального распределения, распределение Стьюдента или как его еще называют t -распределение является функцией переменной t и числа степеней свободы .

Значения t -распределения рассчитаны и табулированы (см. Приложение 2). Кроме того, функция распределения Стьюдента реализована во всех известных компьютерных статистических пакетах.

Смысл использования t -распределения раскрывается выражением

где m - математическое ожидание случайной величины x , m* - статистическая оценка математического ожидания случайной величины x , s - среднеквадратическое отклонение случайной величины x , t - критическое

значение t -распределения для заданного объема выборки и доверительной

1) Известен объем выборки n и задана доверительная вероятность результата. Значение t определяется из таблиц распределения Стьюдента и

рассчитывается доверительный интервал s * t ;

2) Заданы доверительный интервал s * t и объем выборки. Определяется

вероятность попадания случайной величины в доверительный интервал.

На практике часто используют не таблицы распределения Стьюдента, а таблицы критических точек функции распределения. То есть рассматривается вероятность попадания в «хвосты» распределения - 1 - вероятность

96

маловероятного события. Величину обычно выражают в процентах и называют «значимостью».

Степень свободы статистического параметра -

число степеней свободы определяется объемом выборки наблюдений и числом линейных связей между ними; если n выборочных наблюдений связаны k линейными уравнениями, то их распределение имеет n k степеней свободы.

Ранги и ранжирование

Во многих случаях имеющиеся в нашем распоряжении числовые данные (например, значения элементов выборки) носят в той или иной мере условный характер. Например, эти данные могут быть тестовыми баллами, экспертными оценками, данными о вкусовых или политических предпочтениях опрошенных людей и т.д. Анализ таких данных требует особой осторожности, поскольку многие предпосылки классических статистических методов (например, предположения о каком-либо конкретном, скажем нормальном, законе распределения) для них не выполняются. Твердую основу для выводов здесь дают только соотношения между наблюдениями типа «больше-меньше», так как они не меняются при изменении шкалы измерений. Например, при анализе анкет с данными о симпатиях избирателей к политическим деятелям мы можем сказать, что политик, получивший больший балл в анкете, более симпатичен отвечавшему на вопросы человеку (респонденту), чем политик, получивший меньший балл. Но на сколько (или во сколько раз) он более симпатичен, сказать нельзя, так как для предпочтений нет объективной единицы измерения.

В подобных случаях (которые мы будем более подробно рассматривать в последующих главах), имеет смысл вообще отказаться от анализа конкретных значений данных, а исследовать только информацию об из взаимной упорядоченности. Для этого от исходных числовых данных осуществляют переход к их рангам.

Рангом наблюдения называют тот номер, который получит это наблюдение в упорядоченной совокупности все данных — после их упорядочения по определенному правилу (например, от меньших значений к большим или наоборот).

Чаще всего упорядочение чисел (набор которых составляют упомянутые выше данные) производят от меньших к большим. Именно такое упорядочение и связанное с ним ранжирование (присвоение рангов) имеется в виду в дальнейшем.

Пример: Пусть выборка состоит из чисел 6, 17, 14, 5, 12. Тогда ранг числа 6 оказывается 2, рангом 17 будет 5 и т.д.

Процедура перехода от совокупности наблюдений к последовательности их рангов называется ранжированием. Результат ранжирования называется ранжировкой.

97

Статистические методы, в которых мы делаем выводы о данных на основании их рангов, называются ранговыми. Они получили широкое распространение, так как надежно работают при очень слабы) предположениях об исходных данных (не требуя, например, чтобы эти данные имели какой-либо конкретный закон распределения). В последующих главах этой книги мы рассмотрим применение ранговых методов в наиболее распространенных практических задачах.

Трудности в назначении рангов возникают, если среди элементов выборки встречаются совпадающие. (Так часто бывает, когда данные регистрируются с округлением.) В этом случае обыкновенно используют

средние ранги.

Средние ранги вводятся так. Предположим, что наблюдение имеет ту же величину, что и некоторые другие из общего числа N наблюдений. (Эту совокупность одинаковых наблюдений называют связкой, количество таких одинаковых наблюдений в данной связке называют ее размером.) Средний ранг Yk , в ранжировке наблюдений есть среднее арифметическое тех рангов,

которые были бы назначены и всем остальным элементам связки, если бы одинаковые наблюдения оказались различны. Пример расчетов средних рангов показан в Таблице П 3.1 ниже

Таблица П 3.1 Пример расчетов рангов лет и рангов уровней временного ряда

98

Приложение 4

ОЦЕНКА ПАРАМЕТРОВ ЭКОНОМЕТРИЧЕСКИХ МОДЕЛЕЙ НА КОМПЬЮТЕРЕ

Применение средств Microsoft Office для расчетов параметров моделей регрессии

Расчет коэффициентов эконометрического уравнения и статистических оценок модели является сложным вычислительным процессом и требует специальных знаний. Поэтому для эффективной работы над построением моделей желательно использовать специальные статистические программы. Но если таких программ в распоряжении специалиста нет, то могут быть использованы средства Microsoft Office.

«Автоматизировать» процесс расчетов коэффициентов уравнения регрессии и статистических оценок уравнения позволяют электронные таблицы Excel - приложение Microsoft Office. Электронные таблицы Excel располагают:

встроенными функциями для статистических расчетов и расчетов параметров регрессии;

надстройкой «Анализ данных»

Электронные таблицы Excel имеет несколько видов встроенных функций, предназначенных для оценки параметров уравнений регрессии МНК и построения прогнозов: ЛИНЕЙН, ТЕНДЕНЦИЯ. Кроме того, для оценки значимости модели в целом и объясняющих переменной каждой в отдельности можно использовать специальные статистические функции для вычисления критических значений статистик. Такими функциями являются FРАСПОБР, СТЬЮДРАСПОБР. Все перечисленные функции принадлежат разделу встроенных функций «статистические».

Функция ЛИНЕЙН предназначена для расчета коэффициентов линейного уравнения множественной регрессии МНК

Yt a b1 X1t b2 X 2t b3 X3t .... bN X Nt

и статистики МНК оценок.

Для проведения расчетов с помощью функции ЛИНЕЙН необходимо расположить на рабочем листе Excel таблицу с исходными данными. Выборки значений объясняемой переменной и объясняющих переменных необходимо расположить либо строками, либо столбцами.

Если выборка наблюдаемых значений объясняемой переменной располагается в столбце таблицы, то объясняемые переменные X i t следует

99

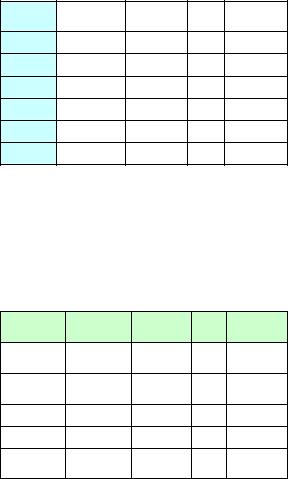
расположить в смежных столбцах. Причем каждый столбец интерпретируется как отдельная переменная (см. Таблицу П 4.1).

Если выборка наблюдаемых значений объясняемой переменной Yt

располагается в строке таблицы, то объясняемые переменные X i t следует

расположить в смежных строках. Причем каждая строка интерпретируется как отдельная переменная(см. Таблицу П 4.2).

константа - логическая переменная, определяющая включается ли в модель свободный член a : если константа принимает значение ИСТИНА, то a вычисляется обычным образом, если константа принимает значение ЛОЖЬ, то a 0;

статистика - логическая переменная, определяющая, требуется ли вычислить статистики МНК оценок: если статистика принимает значение ИСТИНА, функция вычисляет среднеквадратические отклонения коэффициентов

регрессии Sa , Sbi , коэффициент детерминации Ryx2 1x2 ..xm , F - статистику, число

100