
- •Введение Литература
- •Сокращения
- •Тема № 1. Основные понятия программирования
- •1.1. Состав программы на языкеPascal
- •1.2. Элементы программы в языкеPascal
- •1.3. Типы данных в языкеPascal
- •1.4. Операции в языкеPascal
- •1.5. Выражения в языкеPascal
- •1.6. Стандартные функции в языкеPascal
- •1.7. Операторы языка Pascal
- •Тема № 2. Программирование базовых алгоритмов
- •2.1. Программирование последовательных вычислений
- •2.2. Программирование разветвлений
- •2.3. Программирование циклов
- •Тема № 3. Программирование задач с массивами
- •3.1. Одномерные массивы
- •Фрагменты вычисления характеристик одномерного массива
- •Фрагменты операций с одномерными массивами
- •Особенности элементов одномерного массива
- •3.2. Двумерные массивы
- •Фрагменты вычисления характеристик двумерного массива
- •Фрагменты вычисления характеристик строк и столбцов двумерного массива
- •Фрагменты операций с двумерными массивами
- •Особенности элементов квадратных матриц
- •3.3. Перестановка и сортировка элементов массива
- •Тема № 4. Программирование подпрограмм и структурных типов данных
- •4.1. Подпрограммы
- •4.2. Программирование задач с функциями
- •4.3. Программирование задач с процедурами
- •4.4. Программирование задач с файлами
- •4.5. Программирование задач с символами и строками
- •4.6. Программирование задач с записями
- •4.7. Программирование задач со множествами
- •Тема № 5. Моделирование
- •5.1. Моделирование как метод познания
- •5.2. Классификация моделей
- •5.3. Задачи и методы моделирования
- •5.4. Виды численных методов
- •Тема № 6. Введение в компьютерную графику
- •6.1. Предмет компьютерной графики
- •6.2. Виды компьютерной графики
- •6.3. Направления компьютерной графики
- •Тема № 7. Модели компьютерной графики
- •7.1. Геометрические модели
- •7.2. Цветовые и оптические модели
- •Тема № 8. Аффинные преобразования
- •8.1. Общий вид двумерных преобразований
- •8.2. Элементарные двумерные преобразования
- •8.3. Однородные координаты на плоскости
- •8.4. Композиции двумерных преобразований
- •8.5. Преобразования систем координат
- •8.6. Двумерные преобразования на экране монитора
- •8.7. Матричное представление трёхмерных преобразований
8.3. Однородные координаты на плоскости
Перенос реализуется с помощью операции сложения матриц, а масштабирование и поворот – с помощью операции умножения. Это вызывает неудобство при осуществлении нескольких преобразований над объектом.
Пример.Если
объект имеет N
точек и необходимо провести 3
последовательных преобразования, то
понадобится
 действий. Если бы можно было найти
результирующую матрицу с помощью 2-х
операций умножения матриц, то количество
действий стало бы
действий. Если бы можно было найти
результирующую матрицу с помощью 2-х
операций умножения матриц, то количество
действий стало бы .
.
Если выразить положение точек в однородных
координатах, то все элементарные
преобразования можно реализовать с
помощью операции умножения, что при
большом количестве точек даёт ощутимое
преимущество. В однородных координатах
точка
 записывается как
записывается как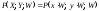 ,
гдеW– дополнительная
фиктивная координата. Причём в декартовой
и однородной системах координаты связаны
соотношениями:
,
гдеW– дополнительная
фиктивная координата. Причём в декартовой
и однородной системах координаты связаны
соотношениями:

где
 .
Если
.
Если ,
то
,
то и
и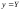 ,
откуда
,
откуда .
.
Основные преобразования точки
 в точку
в точку в однородных координатах выражаются
следующим образом.
в однородных координатах выражаются
следующим образом.
Перенос.
Уравнение переноса запишется в матричном виде следующим образом:
 или
или ,
,
где
 – матрица переноса в однородных
координатах на плоскости.
– матрица переноса в однородных
координатах на плоскости.
Пример.Дан
отрезок с начальной точкой
 и конечной точкой
и конечной точкой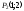 .
Перенести отрезок на 3 единицы вправо
и 2 единицы вниз.
.
Перенести отрезок на 3 единицы вправо
и 2 единицы вниз.
По
условию задачи
 ,
,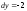 .
Получим результирующие точки в матричном
виде в однородных координатах:
.
Получим результирующие точки в матричном
виде в однородных координатах:
 ;
;
 .
.
Таким
образом, координаты отрезка после
переноса будут
 и
и .
.
Масштабирование.
Уравнение масштабирования в матричной форме имеет вид:
 или
или ,
,
где
 – матрица масштабирования в однородных
координатах на плоскости.
– матрица масштабирования в однородных
координатах на плоскости.
Пример.Дан
отрезок с начальной точкой
 и конечной точкой
и конечной точкой .
Растянуть отрезок в 3 раза по осиx
и сжать в 2 раза по оси y.
.
Растянуть отрезок в 3 раза по осиx
и сжать в 2 раза по оси y.
По
условию задачи
 ,
, .
Итоговые координаты для 1-й точки
останутся прежними. Найдём итоговые
координаты для 2-й точки в матричном
виде в однородных координатах:
.
Итоговые координаты для 1-й точки
останутся прежними. Найдём итоговые
координаты для 2-й точки в матричном
виде в однородных координатах:
 .
.
Таким
образом, координаты отрезка после
масштабирования будут
 и
и .
.
Поворот.
Уравнение поворота можно представить в виде:
 или
или ,
,
где
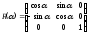 – матрица поворота в однородных
координатах на плоскости.
– матрица поворота в однородных
координатах на плоскости.
Пример.Дан
отрезок с начальной точкой
 и конечной точкой
и конечной точкой .
Повернуть отрезок
на 90
против часовой стрелки.
.
Повернуть отрезок
на 90
против часовой стрелки.
По
условию задачи
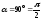 ,
, ,
, .
Итоговые координаты для 1-й точки
останутся прежними. Найдём итоговые
координаты для 2-й точки в матричном
виде в однородных координатах:
.
Итоговые координаты для 1-й точки
останутся прежними. Найдём итоговые
координаты для 2-й точки в матричном
виде в однородных координатах:
 .
.
Таким
образом, координаты отрезка после
поворота будут
 и
и .
.
8.4. Композиции двумерных преобразований
Обычно при работе с графической компьютерной системой объект подвергается сразу нескольким преобразованиям. Более эффективно применять к точкам одно результирующее преобразование, чем ряд последовательных преобразований.
Пример.Повернуть
произвольный объект на угол
вокруг некоторой точки
 .
.
Ранее был рассмотрен поворот относительно начала координат. Для поворота относительно произвольной точки разобьём задачу на 3 этапа:
Перенос точки на
 по осиx
и на
по осиx
и на
 по осиy,
чему соответствует матрица
по осиy,
чему соответствует матрица
 ,
т.е.
,
т.е.
 .
.
Поворот точки на угол относительно начала координат, чему соответствует матрица
 ,
т.е.
,
т.е.
 .
.
Перенос точки на x0 по оси x и на y0 по оси y, чему соответствует матрица
 ,
т.е.
,
т.е.
 .
.
Результирующее преобразование имеет матрицу:
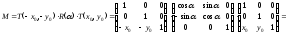
 .
.
В координатном виде данное преобразование можно записать так:

