7.2. Цветовые и оптические модели
В КГ обычно используются следующие цветовые модели:
Модель RGB, где цвет каждой точки представляется суммой красного(Red), зелёного(Green)и синего(Blue)цветов.
Модель CMYK, где цвет каждой точки представляется суммой голубого(Cyan), пурпурного(Magenta), желтого(Yellow)и чёрного(Black, K)цветов.
Модель HSB, где цвет каждой точки представляется суммой цветового тона(Hue), насыщенности(Saturation)и яркости(Brightness).
Модель Lab, где цвет каждой точки представляется суммой светлоты(Lightness), цветности между зелёным и красным(a), а также цветности между синим и жёлтым(b).
В КГ обычно используются следующие оптические модели освещения:
Рассеянное освещение.
Диффузное отражение.
Зеркальное отражение.
Обратное отражение.
Преломление (пропускание света).
Поглощение.
Тема № 8. Аффинные преобразования
8.1. Общий вид двумерных преобразований
При формирований графических изображений
в компьютерных системах постоянно
возникает необходимость изменить
координаты точек на изображении. Пусть
на плоскости точка
с координатамиxиyпреобразуется в точку
с координатами
и
по закону:
или
с помощью матричной функции
.
Обратное преобразование осуществляется по закону:
или
Такие геометрические преобразования называются линейными, если функция преобразованияFявляется линейной функцией относительноxиy:
что можно записать в матричном виде:
.
Линейное геометрическое преобразование координат точек на плоскости называется аффинным, если в результате полученные точки не лежат на одной прямой. Для этого нужно, чтобы уравнения дляfxиfyбыли линейно независимы, а определитель матрицыMбыл бы не равен нулю:
.
8.2. Элементарные двумерные преобразования
В основе изменения графической информации на плоскости лежат 3 элементарных аффинных преобразования.
Перенос(смещение).
Точку на плоскости можно перенести в
новую позицию путём добавления к
координатам этой точки констант переноса.
Для каждой точки
,
которая перемещается в новую точку
,
зададим смещение наdxединиц по осиxи наdyединиц по осиy.
Тогда с помощью прибавления можно
записать:
что в матричном виде будет выглядеть так:
или
,
где
– вектор переноса на плоскости.
При переносе возможны более простые случаи:
если
и
,
то точка будет перемещаться вправо
параллельно осиx;если
и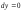
,
то влево;если
и
,
то вверх параллельно осиy;если
и
,
то вниз;если
и
,
то точка будет оставаться на месте.
Пример.Дан
отрезок с начальной точкой
и конечной точкой
.
Перенести отрезок на 3 единицы вправо
и 2 единицы вниз.
По
условию задачи
,
.
Найдём итоговые координаты для 1-й точки:
;
.
Далее найдём итоговые координаты для 2-й точки:
;
.
Таким
образом, координаты отрезка после
переноса будут
и
.
Получим также данный результат в
матричном виде:
;
.
Масштабирование(растяжение, сжатие).
Точку на плоскости можно масштабировать в kxраз по осиxи вkyраз по осиyотносительно начала координат. Получим новую точку с помощью умножения:
что в матричной форме имеет вид:
или
,
где
– матрица масштабирования на плоскости
в декартовых координатах.
При масштабировании возможны простейшие случаи:
если
и
,
то происходит растяжение отрезка от
точки до начала кординат по осиx;если
и
,
то сжатие по осиx;если
и
,
то растяжение по осиy;если
и
,
то сжатие по осиy;если
и
,
то отрезок не меняет размеры;если
и
,
то происходит зеркальное отражение
отрезка относительно прямой
(осиy);если
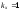и
,
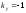то отражение относительно прямой
(осиx);если
и
,
то отражение относительно начала
координат;если
и
,
то отрезок остаётся на месте.
При масштабировании коэффициенты и не должны быть равны нулю, т.к. в противном случае результирующие точки будут лежать на одной прямой.
Пример.Дан
отрезок с начальной точкой
и конечной точкой
.
Растянуть отрезок в 3 раза по осиx
и сжать в 2 раза по оси y.
По
условию задачи
,
.
Итоговые координаты для 1-й точки
останутся прежними. Найдём итоговые
координаты для 2-й точки:
;
.
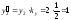Таким
образом, координаты отрезка после
масштабирования будут
и
.
Получим также данный результат в
матричном виде:
.
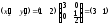Поворот(вращение).
Точка на плоскости может быть повёрнута на угол относительно начала координат. Для этого используем тригонометрические функции:
что в матричном виде можно записать так:
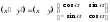или
,
где
– матрица поворота на плоскости в
декартовых координатах.
Обычно угол находится в пределах
в силу периодичности тригонометрических
функций.
При повороте возможны тривиальные случаи:
если
,
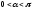то происходит поворот против часовой
стрелки;если
,
то поворот по часовой стрелке;если
,
то происходит зеркальное отражение
относительно начала координат;если
,
то точка остаётся на месте.
В общем случае определитель матрицы поворота всегда равен 1, т.к.
.
Пример.Дан
отрезок с начальной точкой
и конечной точкой
.
Повернуть отрезок
на 90
против часовой стрелки.
По
условию задачи
,
,
.
Итоговые координаты для 1-й точки
останутся прежними. Найдём итоговые
координаты для 2-й точки:
;
.
Таким
образом, координаты отрезка после
поворота будут
и
.
Получим также данный результат в
матричном виде:
.
Можно доказать, что любое аффинное преобразование можно выполнить комбинацией нескольких переносов, масштабирований и поворотов. Но иногда выделяют ещё 2 элементарных преобразования.
Отражение(зеркальное отражение, симметрия).
Точку на плоскости можно симметрично отразить относительно любой прямой или точки. Отражение относительно координатных осей и относительно начала координат является частным случаем масштабирования.
Отражение относительно прямой
(осиy) имеет вид:
или в матричной форме:
.
Отражение относительно прямой
(осиx) имеет вид:
или в матричной форме:
.
Отражение относительно начала координат имеет вид:
или в матричной форме:
.
Отражение относительно начала координат также можно считать поворотом на 180.
Отражение относительно произвольной
прямой
,
не параллельной координатным осям, но
проходящей через начало координат,
записывается в виде:
или в матричной форме:
.
В общем случае определитель матрицы
отражения относительно прямой всегда
равен
.
Пример.Дан
отрезок с начальной точкой
и конечной точкой
.
Отразить отрезок относительно осиx
(прямой
).
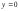Итоговые координаты для 1-й точки останутся прежними. Найдём итоговые координаты для 2-й точки:
;
.
Таким
образом, координаты отрезка после
отражения будут
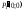и
.
Получим также данный результат в
матричном виде:
.
Сдвиг(скос, наклон).
На плоскости одни точки у объекта могут быть сдвинуты, а другие могут оставаться на месте. Такое преобразование называется сдвигом и математически записывается следующим образом:
или в матричной форме:
.
При сдвиге возможны более простые случаи:
если
и
,
то координатаxу
точки не изменяется, а координатаyбудет изменена везде, кроме прямой
(осиy);если
и
,
то координатаyу
точки не изменяется, а координатаxбудет изменена везде, кроме прямой
(осиx);если
и
,
то точка остаётся на месте.
Пример.Дан
квадрат с угловыми точками
,
,
,
.
Сдвинуть правую сторону квадрата на 1
единицу вверх.
По
условию задачи
,
.
Найдём итоговые координаты для всех
точек в матричном виде:
.
Таким
образом, координаты угловых точек
квадрата после сдвига будут
,
,
,
.