Переменные состояния и фазовые траектории

Возвращаясь к уравнению Ферхюльста, отметим тот очевидный факт, что состояние системы, описываемой рассматриваемым ДУ, в каждый момент времени полностью описывается двумя переменными: и. Начальные значения этих переменных в момент времени:и(при неизменных коэффициентахq и K ) полностью определяют всю последующую динамику их изменения. В теории автоматического управления, широко использующей ДУ, такие переменные принято называть переменными состояния системы. Таким образом, практическим результатом решения ДУ является набор зависимостей переменных состояния от времени. В данном случае таких зависимостей две: и. Их графики, построенные дляимеют вид:

Помимо изображения графиков переменных состояния во временной области (т. е. их зависимостей от времени) удобным средством качественного анализа моделей, описываемых ДУ, является их изображение на фазовой плоскости (или, в общем случае, в фазовом пространстве), т. е. график зависимости одной переменной состояния от другой – фазовой траектории. Для тех же значений параметров модели фазовая траектория будет иметь вид:

Текущему состоянию системы соответствует перемещающаяся по фазовой траектории точка (изображение текущего состояния системы). На фазовой траектории всегда необходимо отмечать направление движения изображающей точки, соответствующее реальному развитие процесса во времени.

Множество всех возможных фазовых траекторий, характерных для системы при различных начальных условиях образует фазовый портрет системы. Ни одна траектория, входящая в состав фазового портрета, в полном фазовом пространстве не пересекает никакую другую – это следует из фундаментального свойства о единственности решения ДУ при одних и тех же начальных условиях.

Системы дифференциальных уравнений. Модель «хищник – жертва»

Особенно ценным аналитический инструмент фазовых траекторий является в случае, если модель описывается ДУ степени >1 или, что то же, системой ДУ первой степени. В этом случае для модели характерны изменения переменных состояния по периодическому закону и фазовая траектория приобретает вид замкнутой криволинейной фигуры.

Так, например, система автономных ДУ первого порядка в общем виде будет выглядеть как:

Рассмотрим пример. Для исследования процессов в системе из двух популяций, одна из которых является пищей для другой, была предложена модель «хищник – жертва» (модель Вольтера-Лотка, 1925 г.). Пусть x₁ – численность популяции «зайцев» (жертв), а x₂ – численность популяции «волков» (хищников). Модель представляет собой систему двух линейных ДУ следующего вида:

где -скорость размножения популяции жертвы в отсутствие хищника (как быстро будет увеличиваться количество зайцев, если все волки вымрут);

- скорость потребления популяцией хищника популяции жертвы (сколько зайцев съедает один волк за единицу времени);

- естественная смертность хищника (какая часть популяции волков умирает в единицу времени от естественных причин);

- коэффициент переработки потребленной хищником биомассы жертвы в биомассу потомства (сколько зайцев должна съесть одна пара волков, чтобы произвести на свет одну пару потомства).

Стационарные состояния определяется путем решения системы алгебраических уравнений (характеристические уравнения):

Таких точек в области действительных чисел две: и

Решения данной системы ДУ в окрестности ненулевого стационарного состояния будут иметь колебательный характер, например, такой:

На фазовой плоскости с осями x₁, x₂ возможные траектории движения изображающей точки (аттракторы) выглядят следующим образом:

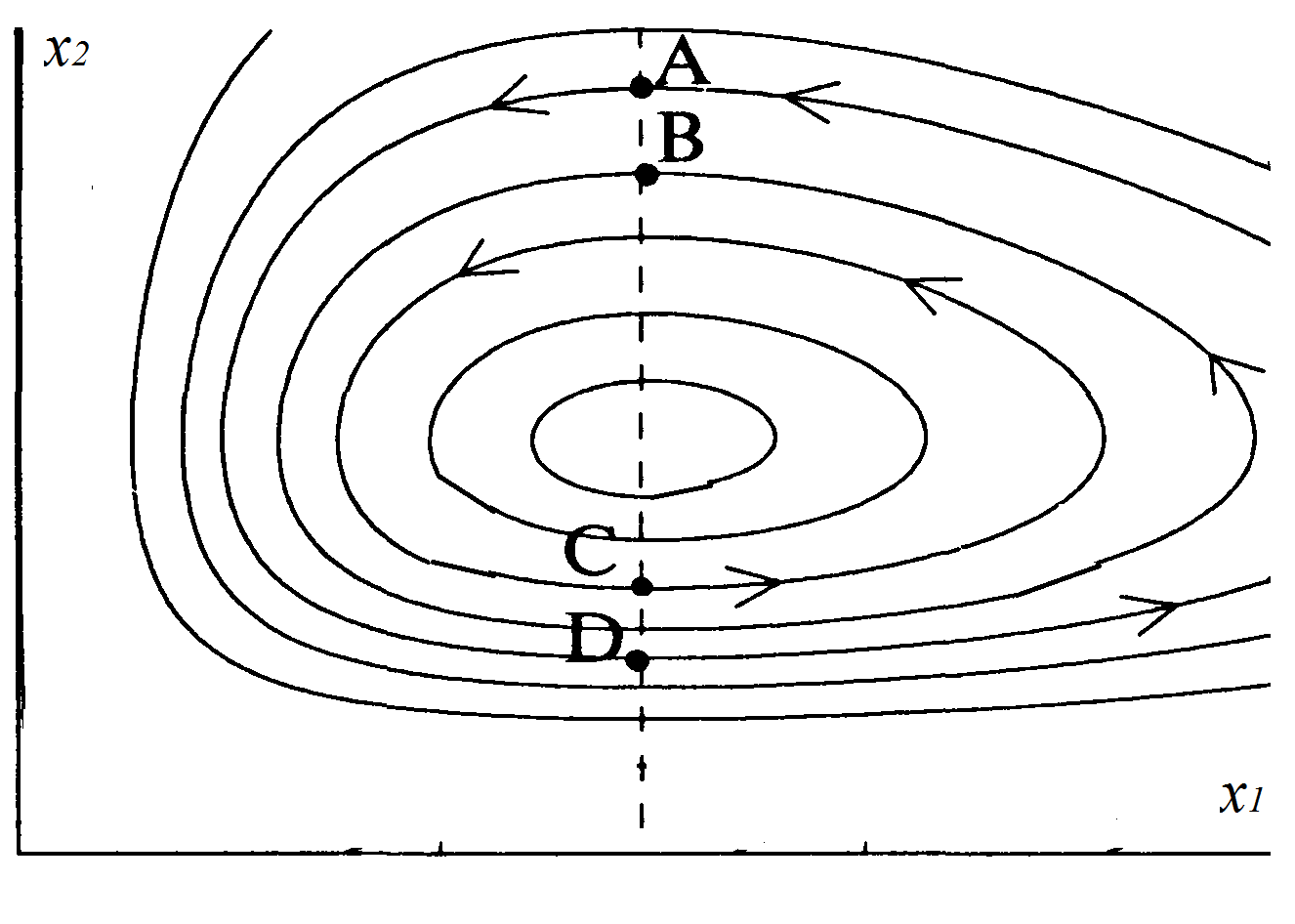
Отметим интересный эффект, многократно подмеченный в живой природе, а впоследствии подтвержденный результатами моделирования. Пусть в системе «хищник – жертва» установился колебательный режим, описываемый аттрактором BC на фазовой плоскости. Предположим, что в момент времени, когда система находилась в точке C (численность хищников – минимальная) произведено принудительное уничтожение (отстрел) некоторого количества хищников. В результате изображающая точка переместилась вниз (точка D) и движется теперь по новому аттрактору AD. Заметим, что амплитуда колебаний численности хищников теперь увеличилась и по прошествии половины полного цикла колебаний система перейдет в точку A. Таким образом, налицо кажущийся парадокс – в результате отстрела пиковая численность хищников не только быстро восстановилась, но и увеличилась (!) по сравнению с первоначальным значением.

На самом деле никакого парадокса здесь нет. Попробуем рассуждать логически. Резко снизив количество хищников, мы тем самым дали толчок росту популяции жертв. Увеличение числа жертв в свою очередь способствовало значительному «улучшению питания» сильно поредевшей популяции хищников, что позволило ей резко повысить рождаемость и в короткие сроки не только восстановить, но и превзойти первоначальную пиковую численность.

Заметим, что анализ фазовых траекторий процесса позволил в данном случае прийти к правильному выводу автоматически, без каких-либо логических размышлений. Это лишь один из примеров, подтверждающий полезность математического моделирования при изучении процессов, протекающих в живой природе.