Инструментальные средства моделирования
Применительно к компьютеру инструментальными средствами математического моделирования могут являться все известные на сегодняшний день языки программирования. В последнее время разработан целый ряд интегрированных сред высокоуровнего программирования, специально предназначенных для сложных математических расчетов: MatCAD, Matlab, Mathematica. Такие программы являются идеальным средством для построения математических моделей, позволяющим максимально упростить их разработку за счет использования колоссальных встроенных библиотек готовых математических подпрограмм. Особо следует отметить, входящий в состав пакета Matlab набор дополнительных модулей Simulink, позволяющий строить модели визуальным способом, из готовых стандартных блоков, не прибегая к традиционному программированию.
Вообще, пакет Matlab стал в последние годы стандартом де факто для научных расчетов в самом широком спектре дисциплин. Поскольку Matlab является коммерческим и весьма дорогостоящим программным продуктом, широкое распространение, особенно в университетской науке, получили его свободно распространяемые независимые клоны – SciLab и GNU Octave.
Лекция 2. Модели, описываемые дифференциальными уравнениями Статические и динамические модели
Модели простейших объектов, как правило, являются статическими, то есть состояние выходов модели в любой момент времени определяется только текущим состоянием ее входов. То есть, в какой бы момент времени мы ни измеряли бы значение выходной величины, при одинаковом значении входного сигнала результат всегда будет один и тот же, вне зависимости от того, что происходило с моделью раньше. Можно сказать, что статическая модель не обладает «памятью».
Пример: модель делителя напряжения.
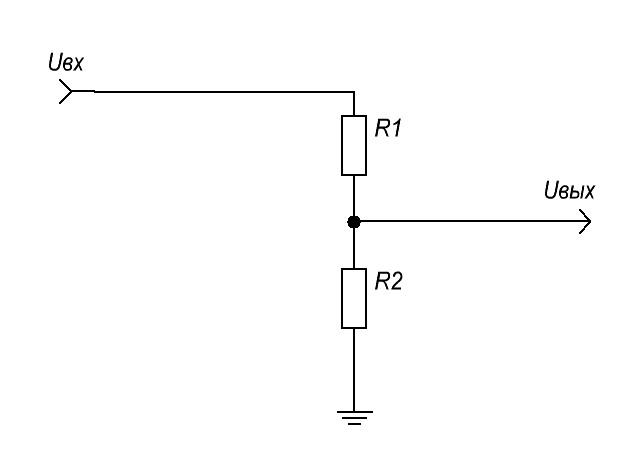
Если значение на выходе модели, при одном и том же входном значении может принимать разные значения в зависимости от того, какие значения подавались на вход раньше, то такая модель называется динамической.
Пример: интегрирующая RC-цепь
,
или:
Как видно из приведенного примера, динамическая модель, в отличие от статической, «помнит» свое прошлое состояние. Это свойство вызвано наличием в математической записи модели производной, связывающей прошлое состояние системы с настоящим. В данной лекции рассматриваются динамические модели, то есть модели, описываемые дифференциальными уравнениями (ДУ).
Простейшие модели, описываемые ду первого порядка: уравнения Мальтуса и Ферхюльста
Принципиальный шаг в математическом моделировании явлений природы был сделан 300 лет назад Ньютоном. Именно он предложил для описания динамических систем математический язык ДУ. Свое развитие этот язык получил в работах Лапласа, Эйлера, Коши. Все современные науки (в том числе и биология) используют ДУ и в этом смысле они являются универсальным средством математического моделирования.
Простейшим видом ДУ является автономное ДУ первого порядка:
.
Его решение (т. е. получение зависимости x(t)) находят путем интегрирования обеих частей уравнения по t, то есть:
,
где C – произвольная константа.
Таким ДУ, например, описывается рассмотренная ранее модель Мальтуса:
,
где x – количество членов популяции, q – коэффициент рождаемости.
Разделим переменные и проинтегрируем:
,
,
В данном случае физический смысл константы С – начальная численность популяции. Таким образом, обозначив ее как x0, окончательно получим решение ДУ:
Графики этой функции при положительных (размножение) и отрицательных (вымирание) значениях константы q скорости роста представлены ниже:
Рассмотрим еще один пример, который относится к классическим моделям математической экологии. Т. н. «логистическое уравнение» было предложено Ферхюльстом в 1838 г. Оно имеет вид:
,
где K – постоянный коэффициент.
Это уравнение, как и рассмотренное выше, можно решить аналитически.
Приведем сразу решение, опустив детали его получения:
,
при начальных
условиях в момент времени
:
и
:
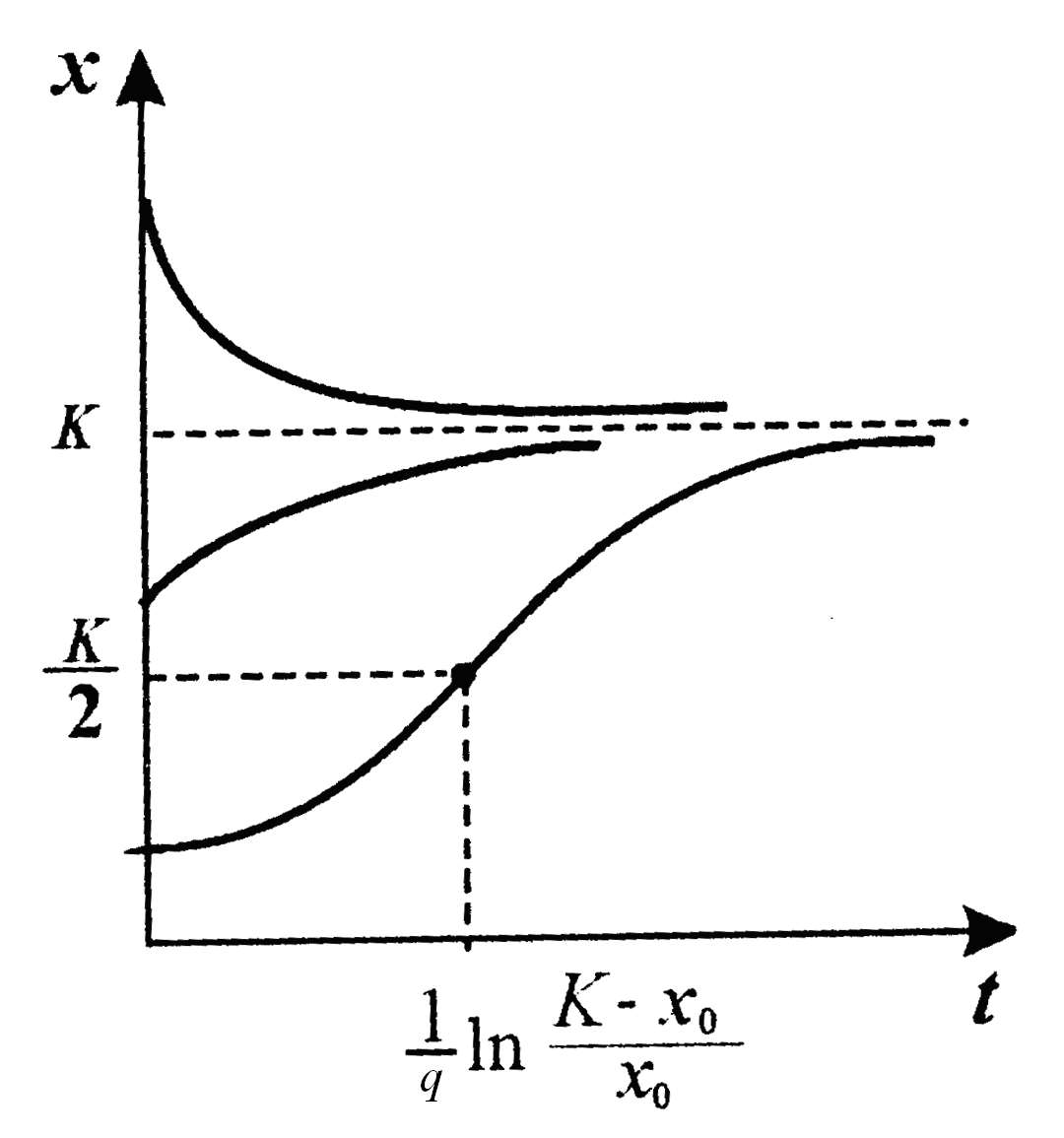
Полученное решение обладает следующими важными свойствами:
1) Если начальный
размер популяции небольшой (
),
то ее численностьх
быстро возрастает, но по мере увеличения
ее рост замедляется (перегиб в точке
),
при этом численность приближается снизу
к пределу, определяемому коэффициентомK.
2) При среднем
начальном размере популяции (
)
численность плавно (без перегиба)
возрастает, приближаясь снизу к пределу,
определяемому коэффициентомK.
3) При большом
начальном размере популяции (
)
численность убывает, приближаясь к
пределу, определяемому коэффициентомK,
снизу.
Данная модель хорошо отображает динамику колонии простейших микроорганизмов в условиях ограниченных пищевых ресурсов. Если численность популяции превышает некоторое пороговое значение, то в условиях нехватки питания среди членов колонии увеличивается смертность и замедляются процессы размножения.