6.1 Основные задачи преобразования

^{Таблица 3 – Основные задачи преобразования комплексного чертежа}

Способ плоско-параллельного перемещения
Номер задачи	Комплексный чертеж	Схема решения	Область применения
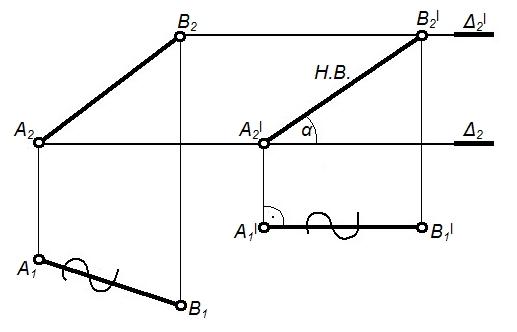
Первая – перевод прямой общего положения в линию уровня		Располагаем AB║П2, тогда располагаем А1B1'  вертикальным лин. связи; A1'B1'= A1B1, т.к. угол α-const.	Определение натуральной величины отрезка прямой линии и углов ее наклона к плоскостям проекций
Вторая – перевод линии уровня в проецирующую прямую.		Располагаем AB║П1, тогда назначаем A2'B2'║ в.л. связи. B1'= A1' – точка.	1. Определение натуральных величин расстояний. 2. Определение натуры двугранного угла.
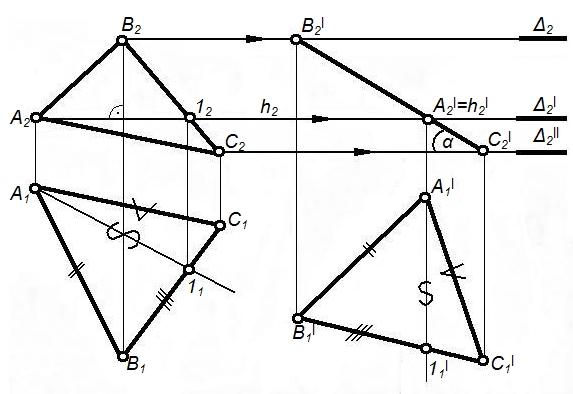
Третья – перевод плоскости общего положения проецирующую плоскость.		Располагаем ∆ABCП2; тогда hП2; Назначаем h1'║ в.л. связи. ∆A1'B1'C1'=∆A1B1C1 т.к. угол α-const. B2'A2'C2' – прямая.	1. Определение натуральной величины углов наклона плоскости к плоскости проекции. 2. Упрощение решения позиционных задач.
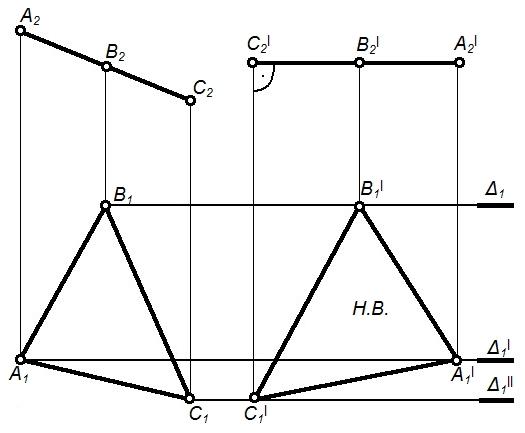
Четвертая – перевод проецирующей плоскости в плоскость уровня.		Располагаем ∆ABC║П1; назначаем C2'B2'A2'  в.л. связи; ∆ C2'A2'B2'=∆ABC – натура плоскости.	Определение натурального вида плоской фигуры, выполнение различных геометрических построений в плоскости фигуры

Способ замены плоскостей проекций
Номер задачи	Комплексный чертеж	Схема решения	Области применения
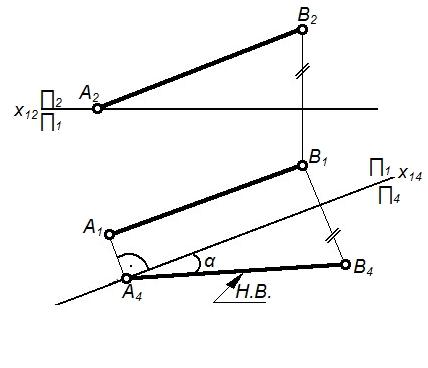
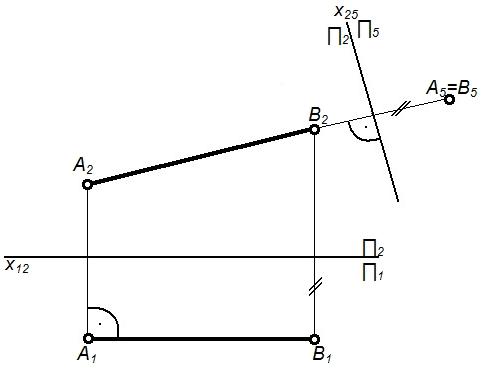
Первая – перевод прямой общего положения в линию уровня		Заменяем П2 на П1; располагаем П4║AB и П4П1; тогда X14║A1B1; A4B4 – натура отрезка.	Определение натуральной величины отрезка прямой линии и углов ее наклона к плоскостям проекций
Вторая – перевод линии уровня в проецирующую прямую.		Заменяем П1 на П5; П5AB; П5П2, тогда X25A2B2. B5= A5 – точка.	1. Определение натуральных величин расстояний. 2. Определение натуры двугранного угла.
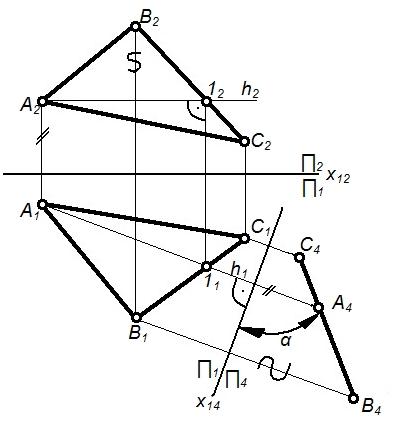
Третья – перевод плоскости общего положения в проецирующую плоскость.		Заменяем П2 на П4; располагаем П4∆ABC, тогда П4h – горизонталь плоскости. Располагаем X14h, A4 B4C4 – прямая, т.е. проецир. пл-ть.	1. Определение натуральной величины углов наклона плоскости к плоскости проекции. 2. Упрощение решения позиционных задач.
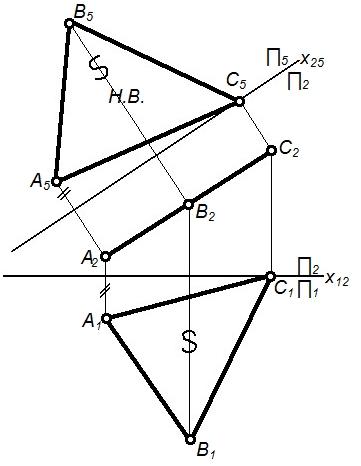
Четвертая – перевод проецирующей плоскости в плоскость уровня.		Заменяем П1 на П5; располагаем П5║∆ABC, тогда X25║A2B2C2; ∆A5B5C5=∆ABC – натура плоскости.	Определение натурального вида плоской фигуры, выполнение различных геометрических построений в плоскости фигуры

^{Изучив и запомнив основы способов плоско-параллельного перемещения и замены плоскостей проекций, следует научиться решать четыре основные задачи преобразования комплексного чертежа (таблица 3). Только после этого можно приступить к решению любых метрических задач.}

^{Метрические задачи делятся на три основных группы:}

^{1 группа – задачи на определение расстояния между геометрическими фигурами.}

^{2 группа – задачи на определение действительных величин плоских фигур и углов.}

^{3 группа – задачи связанные с построением в плоскости общего положения геометрических фигур по заданным размерам.}

^{Приведем примеры.}

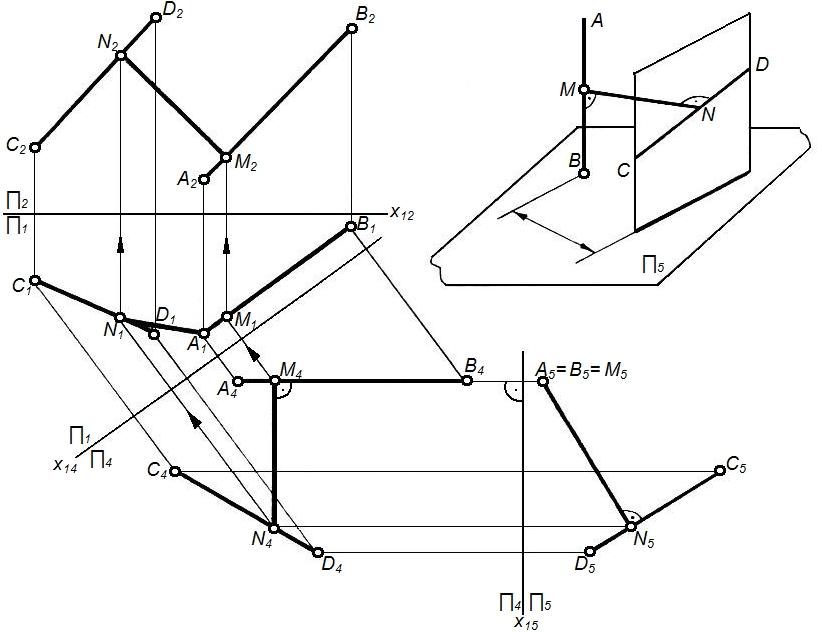
^{Задача №1(1 группа) определить расстояние между скрещивающимися прямымиАВиСD (рисунок 30).}

^{Расстояние между скрещивающимися прямыми выражается длиной перпендикуляра АВиСD(рисунок 30а). Для определения его длины удобно, чтобы одна из прямых (например,АВ) располагалась перпендикулярно плоскости проекций. Для этого надо последовательно ввести две плоскости проекций (рисунок 30б).}

^{Алгоритм решения:}

^{1. 4‖АВ; 4  1; осьX14 ‖А1В1.}

^{2. 5  АВ; 5 4; осьX45  А4В4.}

^{3. АВпроецируется на5в точку (А5 = В5).}

^{4. Опускаем перпендикуляр из точки А5 = В5наС5D5и находимN5.}

^{5. Отметим M5; N5M5– искомое расстояние.}

^{Строим проекции M1N1иM2N2}

^{а) б)}

^{Рисунок 30 – Пример решения метрической задачи №1}

^{Задача №2 (1 группа) Определить расстояние от точки М до плоскости общего положенияθ(А1В1С1, А2В2С2)(рисунок 31).}

^{Если проецировать плоскость θ(А1В1С1, А2В2С2)на плоскостьП4, перпендикулярную кθ, то эта плоскость проецируется в прямуюθ4(рисунок 31а). ПерпендикулярMN, опущенный из точкиМ на плоскостьθ, будет линией уровня по отношению кП4.Поэтому перпендикулярMNпроецируется наП4без искажения, то естьMN=M4N4, причемM4N4перпендикулярнаθ4. Таким образом плоскостьθнадо сделать проецирующей.}

^{Алгоритм решения:}

^{1. Заменяем П2наП4, тогдаθстала проецирующей (рисунок 31б) то есть наП4плоскостьθ– прямая.}

^{2. Опускаем из Мперпендикуляр наθ4.}

^{3. M4N4 – искомое расстояние, причем его натуральная величина.}

^{4. Обратным преобразованием построены проекции М1N1иM2N2отрезкаMN.}

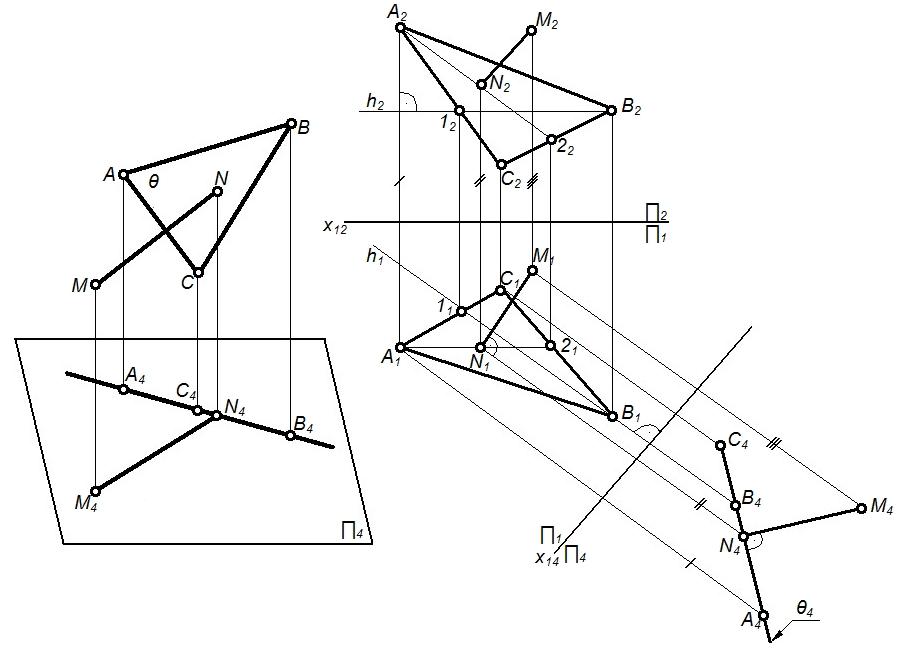
^{а) б)}

^{Рисунок 31 – Пример решения метрической задачи №2}

^{Задача №3(2 группа) Определить величину угла между двумя плоскостями (рисунок 32).}

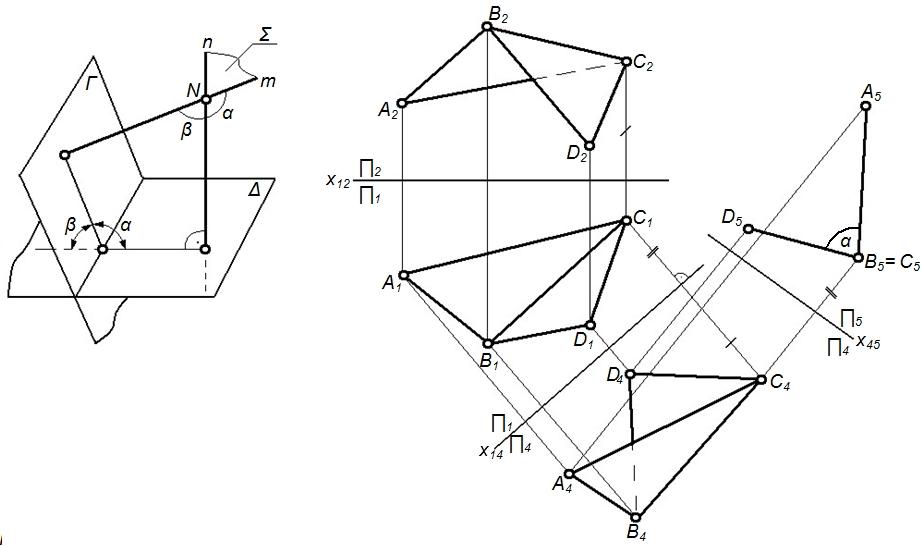
^{а) б)}

^{Рисунок 32 – Пример решения метрической задачи №3}

^{Угол между плоскостями Ги∆(рисунок 32а) измеряется одним из его линейных углов, обычно острым, полученным при пересечении этих плоскостей третьей, перпендикулярной к ним.}

^{Если линия пересечения плоскостей Ги∆ (ребро двугранного угла) не задана, то определения искомого угла требует ряда дополнительных построений. Но их можно избежать, определяя угол, заключенный между перпендикулярамиm иn. Уголявляется искомым если он острый; если же- тупой, то искомый угол = 180 - .}

^{Алгоритм решения следующий:}

^{1. Из точки Nпровестиm  Гиn ∆.}

^{2. Преобразовать плоскость ∑ (m  n)в плоскость уровня.}

^{На рисунке 32б, показано определение двугранного угла, образованного плоскостями Г (АВС)и∆ (ВСD),когда реброВСискомого угла задано. Задача решена преобразованиемВСв проецирующую прямую.}

^{Задача №4(3 группа) В плоскости (a  b)построить равносторонний треугольникАВС, если радиус описанной окружности равенR(рисунок 33).}

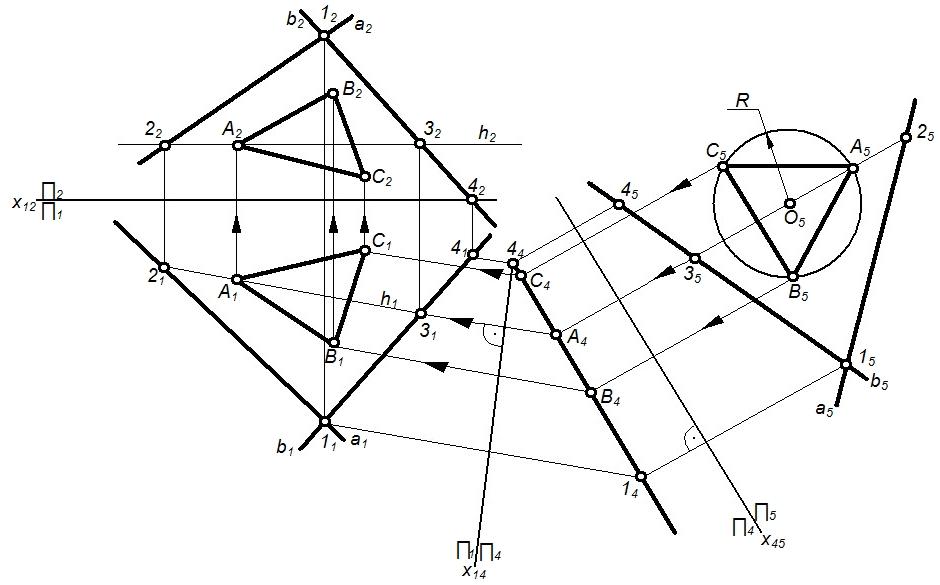
^{Рисунок 33 – Пример решения метрической задачи №4}

^{Алгоритм решения:}

^{1. преобразуем плоскость  (a  b)в плоскость уровня:}

^{а) проводим в плоскости горизонтальh (h1, h2);}

^{б) проводим X14 h1, тогда- проецирующая;}

^{в) проводим X45 ‖(a4, b4),тогда- плоскость уровня.}

^{2. Строим в плоскости уровня равносторонний треугольникА5В5С5,зная радиус описанной окружности.}

^{3. Обратным преобразованием построены проекции А1В1С1иА2В2С2 треугольникаАВС.}