8.8 Построение линии пересечения методом вспомогательных эксцентрических сфер

^{Задача.Построить проекции линии пересечения поверхностей тора() и конуса() (рисунок 75).}

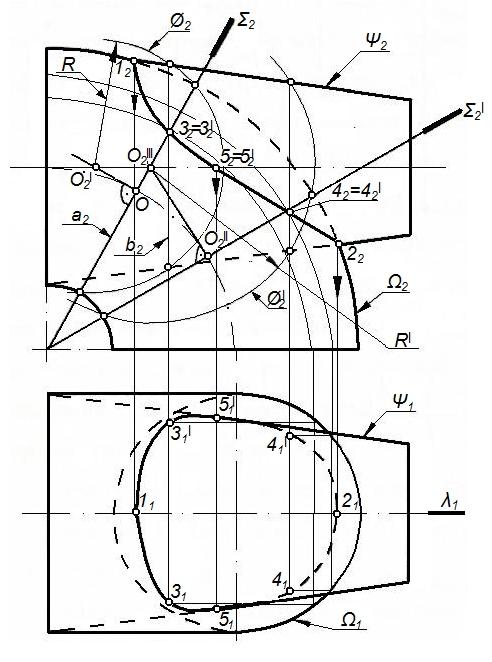
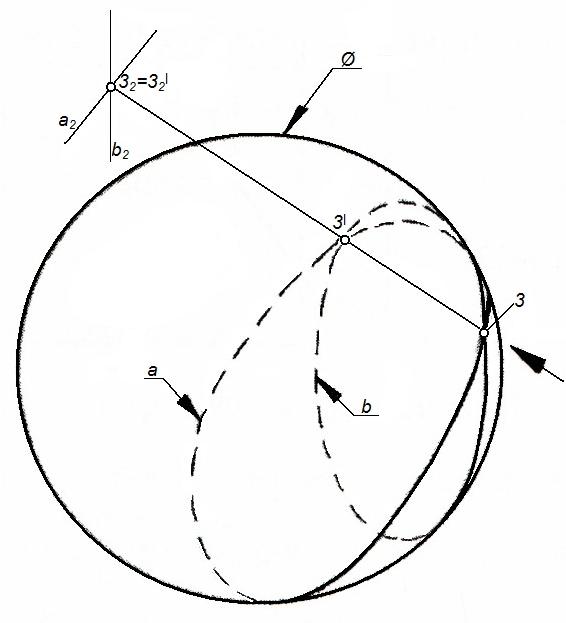
^{Рисунок 75 – Пересечение тора и усеченного конуса}

1. ^{Заданы две поверхности вращения. Оси не пересекаются. Имеется плоскость симметрии ‖П2}

2. ^{Линия пересечения – пространственная замкнутая кривая 1-3-5-4-2-4-5-3-1(рисунок 75).}

3. ^{Опорные точки: 1, 2– экстремальные;3, 3– очерковые относительноП1.}

4. ^{Промежуточные точки: 3,3,4, 4найдены с помощью вспомогательных сферис центрами в точкахОиО,соосных с конусом, содержащих окружности с центром в точкахОиО,принадлежащих тору.}

5. ^{Найденные точки соединены плавной кривой с учетом видимости.}

8.9 Построение линии пересечения второго порядка (частные случаи)

В некоторых случаях кривая, которая получается при пересечении поверхностей вращения, распадается на две плоские кривые, т.е. на кривые второго порядка. Условия, при которых происходит распадение линии пересечения на две плоские кривые, оговариваются в трех теоремах:

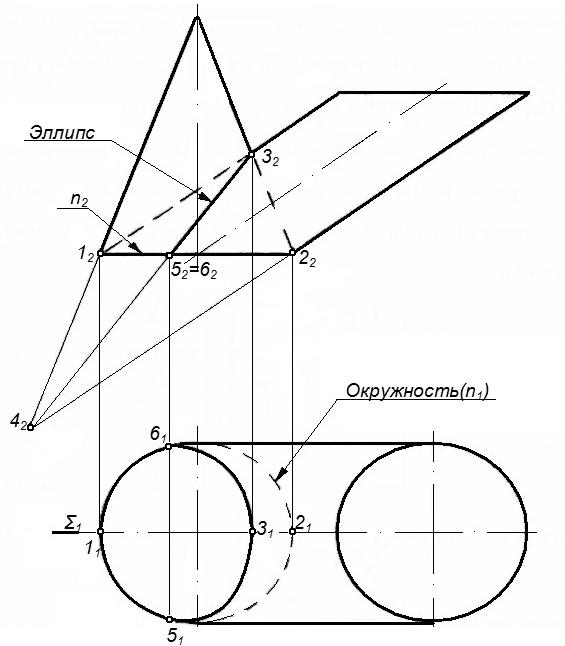
^{Рисунок 76 – Теорема 1}

Теорема 1.Если две поверхности вращения (второго порядка) пересекаются по одной плоской кривой, то они пересекаются и еще по одной плоской кривой (рисунок 76).

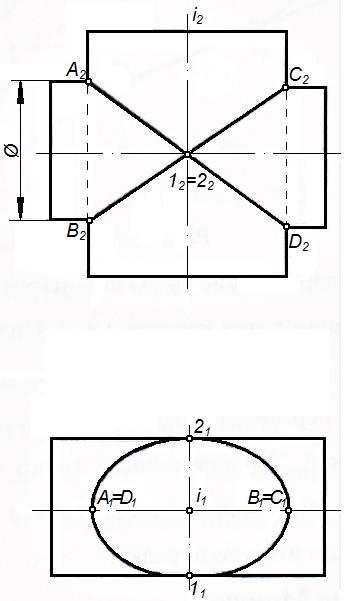
^{Рисунок 77 – Теорема 2}

^{Теорема 2.Если две поверхности второго порядка имеют касание в двух точках, то линия их пересечения распадается на две кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки касания (рисунок 77).}

^{На рисунке показано пересечение двух цилиндров второго порядка. Эти поверхности имеют две общие точки касания 1 и 2. Поэтому по теореме 2 они пересекаются по двум кривым второго порядка.}

^{Теорема 3 (Теорема Монжа). Если две поверхности второго порядка описаны вокруг сферы (или вписаны в нее), то линия их пересечения распадается на две плоские кривые второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания (рисунок 78).}

^{Рисунок 78 – Теорема 3}

^{На рисунке 78 заданы две поверхности вращения (конус и цилиндр), описанные вокруг сферы .}

1. ^{На основании теоремы Монжа искомая линия пересечения распалась на две плоские кривые второго порядка, плоскости которых проходят через прямую KL, соединяющую точки пересечения линий (a) касания сферыи конусаи (b) – касания сферы и цилиндра.}

2. ^{Опорные точки: 1и2– экстремальные (они же очерковые относительноП2);3и3– очерковые относительноП1(они же точки смены видимости наП1)}

3. ^{Промежуточные точки найдены из условия принадлежности.}

4. ^{Найденные точки соединены плавной кривой с учетом видимости.}

8.10 Позиционные задачи на пересечение прямой линии с поверхностью

^{В зависимости от вида и взаимного расположения линии и поверхности точек пересечения может быть одна или несколько. Например, прямая линия с плоскостью пересекается в одной точке, а с кривыми поверхностями в nточках. В основу их построения положен способ вспомогательных секущих плоскостей, сущность которого состоит в том, что каждая из искомых точек рассматривается как результат пересечения двух линий, принадлежащих вспомогательной плоскости. Одна из них является заданной прямой линией, а вторая – линией пересечения вспомогательной плоскости и заданной поверхности.}

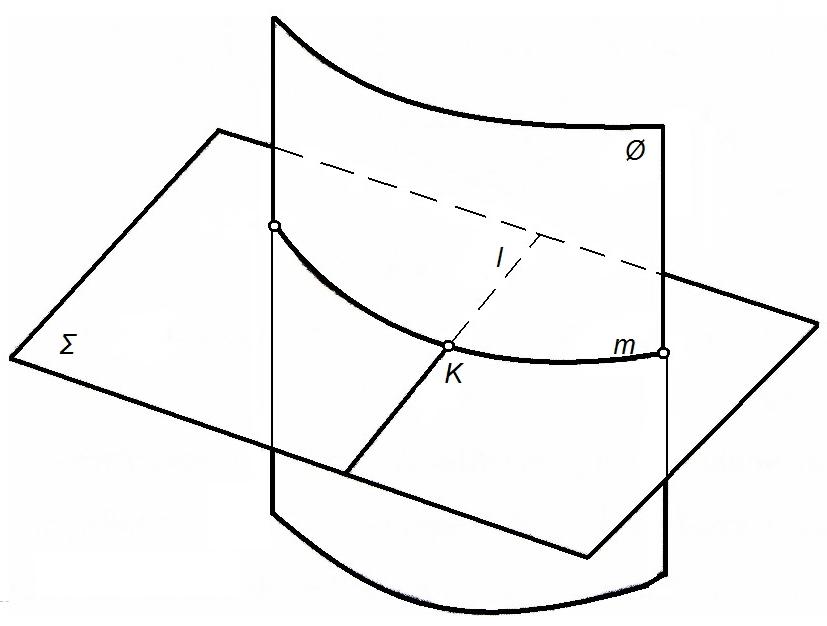
^{Рисунок 79 – Пересечение линии и поверхности}

^{Построение точек пересечения линии lи поверхности(независимо от их вида) осуществляется по общей схеме (рисунок 80).}

^{1. Через lпроводим вспомогательную плоскость.}

^{2. Определяем линию mпересечения вспомогательнойи заданной поверхностей.}

^{3. Отмечаем точку Kпересеченияl иm, которая и является искомой.}

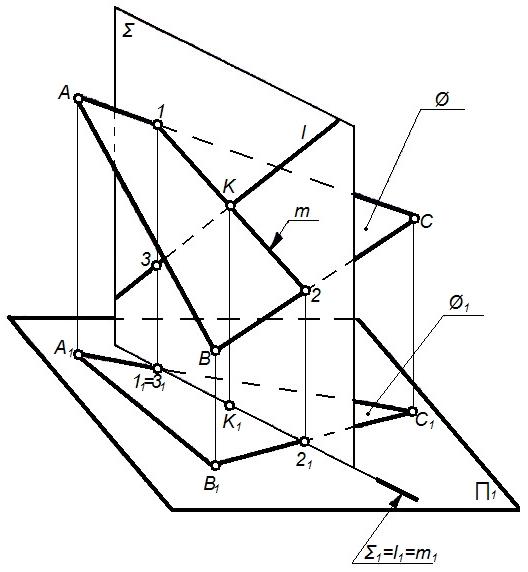
^{Рисунок 80 – Пересечение прямой с плоскостью}

^{Для простоты и точности построения на комплексном чертеже вспомогательную плоскость следует выбирать так, чтобы проекции линии ее пересечения с заданной поверхностью были графически простыми линиями, т.е. прямимы линиями или окружностями.}

^{Ниже рассмотрим примеры решения типовых задач на определение точек пересечение прямой линии и поверхности. Алгоритмы их решения составлены в соответствии с общей схемой решения.}

^{Задача 1. Определение точки пересечения прямой общего положения с плоскостью общего положения.}

^{При определении точки Kпересечения прямойl с плоскостью (АВС)(рисунок 81) в качестве вспомогательной плоскости выбираем проецирующую плоскостьи составим алгоритм решения:}

1. ^{Заключаем прямую lв горизонтально-проецирующую плоскость;}

2. ^{Определяем линию пересечения 1-2плоскостейи;}

3. ^{Отмечаем точку Kпересечения линии1-2иl, которая и является искомой.}

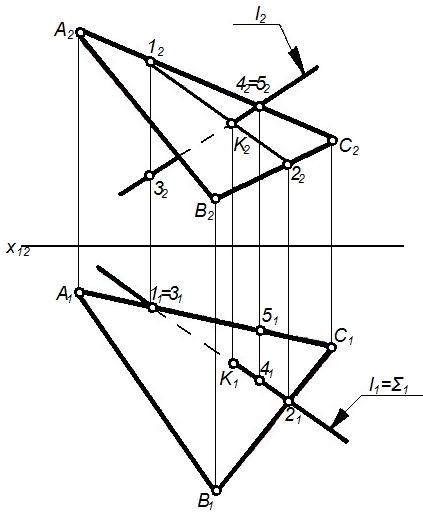
^{Рисунок 81 – Графическое изображение пересечение прямой и плоскости общего положения}

^{Видимость прямой lи заданной поверхностиопределяется с помощью конкурирующих точек. Видимость наП1определена с помощью горизонтально-конкурирующих точек1, 3, а наП2– с помощью фронтально-конкурирующих4, 5. Плоскость (АВС)считается непрозрачной.}

^{Задача 2. Определение точек пересечения прямой линии с поверхностью многогранника.}

^{Решение этой задачи сводится к определению точек пересечения прямой с гранями многогранника и выполняется по предыдущему алгоритму.}

^{Определение точек MиNпересечения прямойlс поверхностью призмы показано на рисунке 82.}

^{Рисунок 82 – Пересечение прямой и призмы}

^{Алгоритм:}

^{1. Прямую lзаключаем в плоскость, П1(может быть выбранаП2);}

^{2. Определяем линию пересечения (1-2-3)плоскостис поверхность;}

^{3. M= (1-2-3)∩l;}

^{4. N=(1-2-3)∩l;}

^{Поверхность многогранника считается непрозрачной. Видимость проекций прямой lопределяется по видимости граней многогранника.}

^{Рассмотренный алгоритм применим для определения точек пересечения прямой с любым многогранником.}

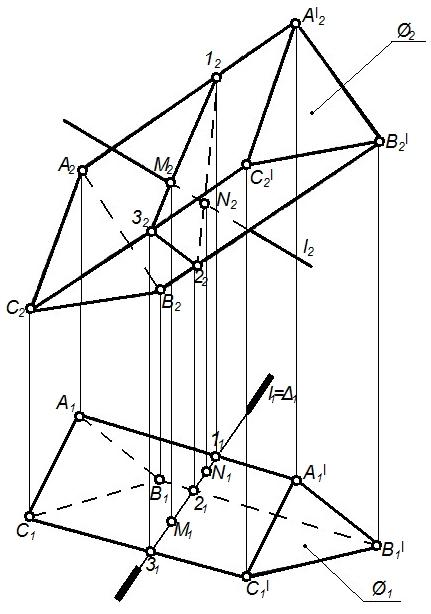
^{Рисунок 83 – Графическое изображение пересечения прямой и призмы}

^{Задача 3. Определение точек пересечения прямой линии с поверхностью конуса.}

^{В задаче (рис.93) требуется определить точки MиNпересечения горизонталиhс поверхностью конуса вращения.}

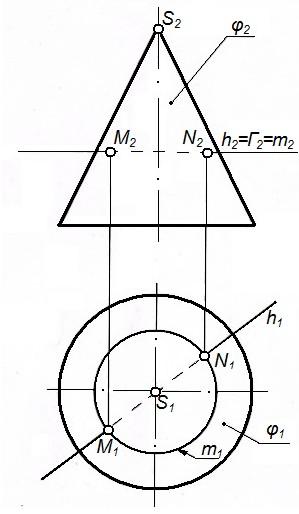
^{Рисунок 84 – Графическое изображение пересечения прямой и конуса}

^{В данном случае целесообразно через прямую hпровести горизонтальную плоскость уровняГ, т.к. она пересечет поверхность конуса по параллелиm, которая проецируется на П1без искажения.}

^{Алгоритм:}

^{1. Заключаем горизонталь h в плоскостьГ (Гh; Г‖П1);}

^{2. При пересечении плоскости Гс конусом получается окружностьm(m=φ∩Г).}

^{3. M=m∩h; N=m∩h.}

^{Задача 4. Определение точек пересечения прямой линии и сферы.}

^{В задаче (рисунок 85) требуется определить точки MиNпересечения сферыӨс фронтальюf. В качестве вспомогательной плоскости целесообразно применить фронтальную плоскость уровня, так как окружностьmсечения сферыӨэтой плоскостью проецируется наП2без искажения.}

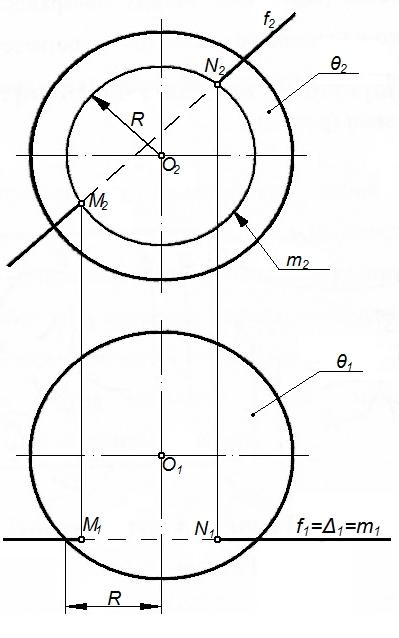
^{Рисунок 85 - Графическое изображение пересечения прямой и сферы}

^{Алгоритм:}

^{1. Заключаем фронталь f в плоскость (f; ‖П2);}

^{2. При пересечении плоскости со сферой получается окружностьm(m=Ө ∩).}

^{3. M=m∩ f; N=m∩ f.}