Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казахский национальный университет им. аль-Фараби

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ЛЕКЦИИ МДТТ РУС

.pdf

Скачиваний:

Добавлен:

24.03.2015

Размер:

722.6 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

4. Раздел № 4 Краткий конспект лекций

Лекционные занятия № 1-2.

Название темы: Диаграмма Мора. Девиатор напряжений. Девиатор деформаций. Интенсивность напряжений. Интенсивность деформаций.

Цель лекций: Дать понятие о кругах Мора; дать представление об обобщенных напряжениях и деформации.

Ключевые слова: диаграмма Мора; интенсивность напряжений; интенсивность деформаций; девиатор напряжений; девиатор деформаций.

Основные вопросы (положения) и краткое содержание:

Вэтих лекционных занятиях будут рассматриваться следующие основные понятия

иположения МДТТ: напряженное состояние; главные напряжения; главные площадки; главные касательные напряжения; гидростатическое давление; девиатор напряжений; инварианты тензора напряжений; главные деформаций; девиатор деформаций; инварианты тензора деформаций; интенсивность деформаций; диаграммы Мора.

Основные схемы, формулы и т.д., иллюстрирующее содержание:

Напряженное состояние

Влюбой точке сплошной среды напряженное состояние характеризуется

симметричным тензором напряжения


				(1.1)
где σx , σy ,σz - нормальные, а τxy , τyz , τxz				- касательные напряжения на площадях,
перпендикулярных к координатным осям x, y, z.
	R
Вектор напряжения pп		на произвольно ориентированной площадке с единичной
R
нормалью n ( Рис. 1) определяется формулами Коши:
px = σx nx + τxy n y + τxz nz ,
	= τxy nx + σyn y		+ τyznz ,	(1.2)
py	= τxy nx + σyn y		+ τyznz ,	(1.2)
	= τxz nx + τyz n y		+ σz nz ,
pz	= τxz nx + τyz n y		+ σz nz ,
где nx , n y , nz - компоненты единичного вектора нормали n .
				R
	R
Проектируя вектор	pп на направление нормали получаем нормальное напряжение σn ,
действующее на данной площадке
σ n = σ x nx2 + σ y ny2 + σ z nz2 +				(1.3)
				(1.3)
+ 2τ xy nx ny + 2τ yz ny nz + 2τ zx nz nx .
Величина касательного напряжения τ n				равна:
τn	= (px2 + p2y + pz2 − σn2 )1 / 2 .			(1.4)

В любой точке сплошной среды существуют такие три взаимно перпендикулярные площадки, на которых касательные напряжения равны нулю. Направления нормалей к этим площадкам образуют главные направления тензора напряжения и не зависят от исходной системы координат x, y, z. Это означает, что любое напряженное состояние в рассматриваемой точке может быть вызвано растяжением окрестности точки в трех взаимно перпендикулярных направлениях. Соответствующие напряжения называются главными нормальными напряжениями; будем обозначать их через σ1,σ2 , σ3 , причем условимся нумеровать главные оси так,

что

σ1 > σ2 > σ3 .

(1.5)

Легко найти по формулам (1.2)-(1.4), что в сечениях, делящих пополам углы между главными плоскостями и проходящих соответственно через главные оси 1, 2, 3 (рис. 2).

Рис. 1

Рис. 2

Касательные напряжения в этих сечениях достигают экстремальных значений и

называются главными касательными напряжениями:

= σ2 − σ3 , τ

= σ3 − σ1 , τ

= σ1 − σ2 .

(1.6)

С изменением ориентации площадки изменяются и величина действующего на

площадке

касательного напряжения

τ n . Наибольшее значение

τ n в

данной

точке

называется

максимальным касательным напряжением τ max .

Если

условие

(1.5)

выполняется, то из (1.6):

= −τ2 = σ1 − σ3 .

τmax

Нормальное напряжение σ n на заданной площадке не зависит, очевидно, от выбора

координатной системы и изменяется лишь при повороте площадки.

Величина

σ =

(σx + σy + σz ),

(1.7)

называется средним (или гидростатическим) давлением в точке.

τi = +

Ι2 (σ€ 2 )

[(σx −σ y )2 +(σ y −σz )2 +(σ z −σx )2 +6(τ xy2 +τ yz2 +τ xz2 )]1/ 2.

(1.8)

называют интенсивностью касательных напряжений.

Интенсивностью напряжений называется величина:

σ =

[(σ1 − σ

2 )2 + (σ

2 − σ3 )2 + (σ3

− σ1 )2 ] 1/ 2.

(1.9)

Диаграмма Мора. Разыскиваются площадки, на которых нормальное и

касательное напряжения имеют заданные наперед значения σn и

τn . Задача сводится к

разысканию трех неизвестных n12 , n 22 , n32 из уравнений (1.2)-(1.4), к которым

добавляется уравнение													n 2			+ n 2				+ n 2	= 1.
														1			2			3
	Искомое решение записывается в виде:
2	=			f1(σn			, τn )							2		=			f2 (σn , τn )
n1										,			n2												,
n1		(σ −σ )(σ −σ )								,			n2					(σ −σ )(σ −σ )							,
			1			2	1	3									2			1	2			3					(1.10)
										f3(σn , τn )																			(1.10)
						n2 =				f3(σn , τn )
						n2 =		(σ3 −σ1)(σ3 −σ2 )
							3	(σ3 −σ1)(σ3 −σ2 )
							3
где обозначено:
	f (σ			, τ		) = τ2		+					−	σ			+ σ			2		σ		− σ				2
	f (σ			, τ		) = τ2		+	σ				−		2		2		3	−			2				3	,
	1		n		n		n					n					2							2
	f2 (σn			, τn ) = τn2 +							σn		−	σ			+ σ			2		σ		− σ				2	(1.11)
	f2 (σn			, τn ) = τn2 +							σn		−			3	2		1	−			3	2		1		,	(1.11)
																	2							2
	f3 (σn			, τn ) = τn2 +							σn		−	σ + σ						2		σ − σ						2
	f3 (σn			, τn ) = τn2 +							σn		−		1		2		2	−		1		2		2		.
																	2							2

Так как выполняется условие (1.5), а левые части этих равенств (1.10) неотрицательны, то должно быть:

f1 > 0, f2 < 0,	f3 > 0,	(1.12)
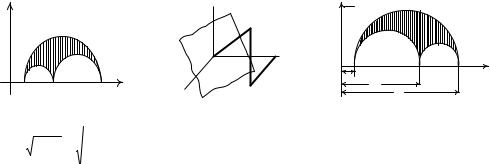
т.к. выражения σn , τn лежат	внутри области,	ограниченный полуокружностями и

заштрихованный на рис. 3; здесь σ 1 ,σ 2 ,σ 3 - главные напряжения (рис. 4).

Деформация.

Деформация сплошной среды характеризуется симметричным тензором деформации

(1.13):

(1.13)

здесь εx , εy ,εz

– относительные удлинения,

γxy , γ yz , γzx –

относительные сдвиги.

Разности

γ 1

= ε 2 − ε 3 , γ 2 = ε 3 − ε1 ,

γ 3 = ε1 − ε 2 ,

(1.14)

называются главными сдвигами.

Здесь

ε1, ε2 , ε3 - называются главными удлинениями

(рис. 5).

Рис. 3

Рис. 4

Рис. 5

1/ 2

γi = +2

Ι2(ε€2)

(εx −εy )2

+(εy −εz )2 +(εz −εx )2

(γxy2 +γyz2 +γzx2 ) .

(1.15)

Вопросы для самоконтроля:

1. Что такое вектор напряжения? 2. Зачем нужна диаграмма Мора? 3. Зачем вводиться понятия интенсивность напряжений и деформация?

Рекомендуемая литература:

1.Работнов Ю.Н. Механика деформируемого твердого тела. - М.: Наука, 1988. - 712с.

2.Искакбаев А. И. Основы механики деформируемого твердого тела. - Алматы: Изд-во Қазақ университетi, 2008. – 216 с.

Лекционные занятия № 3-4.

Название темы: Тензорное условие совместности деформаций Сен-Венана. Линейная модель упругой среды. Потенциальная энергия. Законы Гука. Классические теорий прочности.

Цель лекций: Изложение основы классических теорий прочности. Ключевые слова: константы Ламе; закон Гука; предел прочности; предел

текучести; потенциальная энергия.

Основные вопросы (положения) и краткое содержание:

Вэтих лекционных занятиях будут рассматриваться следующие основные понятия

иположения МДТТ: условие совместности деформаций Сен-Венана; линейная модель упругой среды; упругие потенциалы; основные гипотезы теории прочности.

Основные схемы, формулы и т.д., иллюстрирующее содержание:
̂ 0,	(2.1)
Условия сплошности и условия совместности деформаций:
)	знак транспонирования.
где ε – тензор деформации, а (*) –

Линейная модель упругого тела.

Закон состояния линейно-упругого тела в изотермическом процессе деформирования

	2 ̂,						(2.2)
будем записывать в виде:
	единичный тензор, ε – объемное расширение, а λ,μ –						постоянные упругости
здесь –
		называемые коэффициентами Ламе.
	Закон упругого изменения объема и закон упругого изменения формы
					записываются в виде:
		2 ̂,					(2.4)
	σ = K ε ,						(2.3)

				К объемный модуль упругости:
	K = λ +			2	μ.		(2.5)

		3
	Удельная потенциальная энергия. Упругий потенциал.
	Энергию, накапливаемую при деформации в единичном объеме материала,
выделенном около данной точки, называют удельной потенциальной энергией.
Выражение для определения потенциальной энергии деформации упругого тела
			·· ̂,			записываем в виде:	(2.6)
здесь						̂ – тензор деформации, а

	– тензор напряжений,						(··) – знак скалярного

произведения.

Классические теории прочности.

Теория наибольших нормальных напряжений. В основу этой теории положена следующая гипотеза: прочность будет нарушена, если наибольшие нормальные напряжения превысят некоторые предельные значения, не зависящие от вида

напряженного состояния (гипотеза Галилея). Условие наступления опасного состояния

σ 1 = (σ ΟΠ )+ или σ 3 = (σ ΟΠ ),

(2.7)

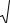
где (σ ΟΠ )+ и (σ ΟΠ ) - предельные (опасные) напряжения при растяжении и сжатии.

Теория наибольших линейных деформаций

В основу этой теории положена следующая гипотеза (гипотеза Мариотта): прочность будет нарушена, если наибольшая по абсолютной величине относительная линейная деформация превысит некоторое предельное значение, независящее от вида напряженного состояния.

Условие наступления опасного состояния запишутся:

εmax E = [σ1 − ν(σ2 + σ3 )] = σb + ,

εmin E = [σ3 − ν(σ1 + σ2 )] = σb −

или

σэкв	σ − ν(σ		+ σ	) = σ	b +	,
σэкв	= 1	2	3		b +		(2.8)
	σ3 − ν(σ1 + σ2 ) = σb − ,
где σэкв –	эквивалентное напряжение, σ b –						предел прочности образца.

С помощью критерия Мариотты можно, например, объяснить разрушение хрупких материалов не только при растяжении и кручении, но и при сжатии.

Теория наибольших касательных напряжений

В основу этой теории положена следующая гипотеза: прочность будет нарушена, если наибольшие касательные напряжения превысят некоторое предельное значение, не зависящее от вида напряженного состояния (гипотеза Кулона-Треска).

Этот критерий был предложен Треска на основании экспериментов по штамповке и прессованию металлов в качестве условия пластичности.

Условие наступления опасного состояния

τ max = τ ΟΠ = τ Τ ,

здесь τT – предел пластичности образца.

Теория полной потенциальной энергии

Воснову этой теории положена следующая гипотеза: прочность будет нарушена, если удельная потенциальная энергия деформации превысит некоторое предельное значение, не зависящее от вида напряженного состояния (гипотеза Бельтрами).

Критерий Бельтрами практически не используется. Многочисленные эксперименты показывают, что при всестороннем равномерном сжатии разрушение (или текучесть) материалов не наступает даже при очень больших напряжениях. В то же время энергия, накопленная в испытуемом образце, значительно превышает опасное значение, полученное в опытах на одноосное растяжение или сжатие.

Теория энергии формоизменения

Воснову этой теории положена следующая гипотеза: прочность будет нарушена, если удельная потенциальная энергия формоизменения превысит некоторое предельное значение, не зависящее от вида напряженного состояния (гипотеза Губера).

Условие наступления опасного состояния имеет вид:


σ	экв	= σ 2	+ σ 2	+ σ 2	− (σ σ	2	+ σ	σ	3	+ σ σ	1	) = σ	ОП	.	(2.9)
	экв	1	2	3	1	2	2		3	3	1		ОП

Критерий Губера получил удовлетворительное экспериментальное подтверждение для разных конструкционных материалов, находящихся в пластичном состоянии и одинаково сопротивляющихся растяжению и сжатию.

Вопросы для самоконтроля:

1.Сколько необходимо констант для описания изотропной линейно-упругой среды?

2.Почему не используется гипотеза Бельтрами?

Рекомендуемая литература:

1. Работнов Ю.Н. Механика деформируемого твердого тела. - М.: Наука, 1988. - 712с.

2. Искакбаев А. И. Основы механики деформируемого твердого тела. - Алматы: Изд-во Қазақ университетi, 2008. – 216 с.

Лекционные занятия № 5-6.

Название темы: Основные соотношения линейной теории упругости. Краевые задачи. Методы решения. Метод перемещений. Дифференциальные уравнения Навье

– Коши – Ламе.

Цель лекций: Вывод уравнений описывающих движение изотропной, однородной упругой среды.

Ключевые слова: законы упругости; соотношения Коши; уравнения движения сплошной среды; методы решения краевых задач теории упругости.

Основные вопросы (положения) и краткое содержание:

В этих лекционных занятиях будут рассматриваться следующие основные понятия и положения МДТТ: основные соотношения линейной теории упругости; краевые задачи; методы решения; метод перемещений; дифференциальные уравнения Навье – Коши – Ламе.

Основные схемы, формулы и т.д., иллюстрирующее содержание:

Основные соотношения линейной теории упругости.

Эти уравнения задаются тремя группами соотношений.
Первая группа представлена уравнениями статики в объеме
0,		(3.1)
	R
где – тензор напряжений, F – вектор объемной силы.
Вторая группа уравнений содержит определение линейного тензора деформации
	R
̂через вектор перемещения u :
̂	u ,	(3.2)

здесь Ñ – набла-оператор, а (*) – знак транспонирования. Здесь имеется шесть уравнений, определяющих компоненты тензора деформации по первым производным трех компонентов вектора перемещения.

В третей группе шести уравнений формулируется закон состояния линейно- упругого тела. Для изотропного тела и в изотермическом или адиабатическом процессах этот закон – обобщенный закон Гука – записывается в форме

	(3.3)
2 ̂,

здесь μ = G - модуль сдвига, ε - объемное расширение.

Краевые условия

В первой задаче ставится кинематическое краевое условие: в объеме V

разыскивается вектор перемещения, принимающий на поверхности S, ограничивающей этот объем, заданное значение

R		R
u	S	= u*	(x1, x2	, x3 ),	(3.4)

здесь координаты x1 , x 2 , x3 связаны уравнением поверхности.

Вторая краевая задача – статическая. Задается распределение поверхностных

сил R , и краевым условием является уравнение равновесия на поверхности S q

	· ,	(3.5)
R	- единичный вектор внешней нормали к поверхности тела.
где n	- единичный вектор внешней нормали к поверхности тела.

Третья краевая задача – смешанная. На части S1 задается кинематическое, а на другой ее части S2 статическое краевое условие.

Известны два способа решения задач теории упругости. В первом начинают с

разыскания вектора перемещения u , по которому уже не представляют затруднения вычислить тензор деформации ̂,а по последнему – тензор напряжения. Второй способ

– способ решения задачи в напряжениях. Тогда ставится вопрос о разыскании такого статически возможного тензора напряжения , что определяемый по нему тензор

R	находится
деформации ̂удовлетворяет условию сплошности. Вектор перемещения u	находится
по формуле Чезаро.

Дифференциальные уравнения теории упругости в перемещениях

Подставляя в уравнение статики (3.1) выражение тензора напряжений (3.3) через

		R
вектор перемещения u (3.2),
приводит к искомому дифференциальному уравнению
1			R	2	R		1	R
		graddivu+ Ñ		2	u+			F = 0 .		(3.6)
1 - 2n		graddivu+ Ñ			u+		m	F = 0 .		(3.6)
1 - 2n							m
Уравнение движения Навье –					Коши - Ламе:
			2 R		¶	2	R
	R		2 R		¶		u
(λ + μ )graddiv u + μÑ			R	ρ ¶t 2
(λ + μ )graddiv u + μÑ			u + F =	ρ ¶t 2				.		(3.7)
Векторное соотношение: rotrotu = graddivu - Ñ2u .										(3.8)
						R		R	R

Вопросы для самоконтроля:

1. При использовании метода перемещения, нужно ли проверять условия Сен- Венана? 2. Можно ли в задачах линейной теории упругости применять принцип суперпозиции?

Рекомендуемая литература:

1.Работнов Ю.Н. Механика деформируемого твердого тела. - М.: Наука, 1988. - 712с.

2.Искакбаев А. И. Основы механики деформируемого твердого тела. - Алматы: Изд-во Қазақ университетi, 2008. – 216 с.

Лекционные занятия № 7-8.

Название темы: Метод сил. Тензорное уравнение Бельтрами – Мичелла. Формула Клапейрона. Теорема Кирхгофа.

Цель лекций: Доказать единственность решений краевых задач линейной теории упругости.

Ключевые слова: условия Сен-Венана; метод сил; условия Бельтрами – Мичелла.

Основные вопросы (положения) и краткое содержание:

В этих лекционных занятиях будут рассматриваться следующие основные понятия и положения МДТТ: метод сил при решении краевых задач теории упругости; установление связи работами внутренних и внешних сил; установление, при каких условиях имеет место единственное решение краевых задач линейной теории упругости.

Основные схемы, формулы и т.д., иллюстрирующее содержание:

Решение в напряжениях. Зависимости Бельтрами - Мичелла

При отсутствии объемных сил первый инвариант тензора напряжений σ будет гармонической функцией:

Ñ2σ = 0.

(4.1)

Тензор напряжений , удовлетворяющий уравнениям статики в объеме, должен быть так выбран, чтобы вычисленный по нему тензор деформации удовлетворял условиям совместности:

!" !" ̂ 0.

(4.2)

Используя уравнение статики, можно преобразовать это соотношение к легко обозримому и запоминаемому виду:

σ 0.

В компонентах в декартовой системе координат:

Ñ2sx

3 ¶2s

= 0,

Ñ2txy

¶2s

= 0,

+ n ¶x2

+ n ¶x¶y

Ñ2sy

3 ¶2s

= 0,

Ñ2tyz

¶2s

= 0,

+ n ¶y2

+ n ¶y¶z

Ñ2sz

3 ¶2s

= 0,

Ñ2tzx

¶2s

= 0.

+ n ¶z2

+ n ¶z¶x

Формула Клапейрона. Теорема Кирхгофа

(4.3)

(4.4)

Потенциальная энергия деформации упругого тела определяется интегралом по объему от удельной потенциальной энергии:

~
U = ∫ Udv.	(4.5)

Эта величина равна половине работы внешних сил на последовательности равновесных состояний линейно-упругого тела из его натурального состояния.

Приведем формулу для дивергенции вектора:

· · ·· ̂.

(4.6)

В итоге приходим к формуле Клапейрона:

~	1		R	R	R	R
U =			∫ F × udv + ∫ q × uds ,				(4.7)
U =	2		∫ F × udv + ∫ q × uds ,				(4.7)
	2	V			S

здесь U - определяется соотношением (4.5).

Теорема Кирхгофа. Вводятся следующие предположения:

1)начальное состояние тела является натуральным;

2)в каждой точке тела удельная потенциальная энергия удовлетворяет условию U > 0 ;

3)допускается общепринятое в линейной теории упругости пренебрежение изменением формы тела при формулировании краевых условий – ограничивающая

упругое тело, поверхность S в состоянии равновесия такая же, как в натуральном состоянии

εij	<< 1,	ωk	<< 1 .	(4.9)

При перечисленных условиях решение краевых задач – единственное (теорема Кирхгофа).

Вопросы для самоконтроля:

1. Когда необходимо использовать условия Бельтрами – Мичелла? 2. При каких условиях нельзя пользоваться теоремой Кирхгофа?

Рекомендуемая литература:

1.Работнов Ю.Н. Механика деформируемого твердого тела. - М.: Наука, 1988. - 712с.

2.Искакбаев А. И. Основы механики деформируемого твердого тела. - Алматы: Изд-во Қазақ университетi, 2008. – 216 с.

Лекционные занятия № 9-10.

Название темы: Плоская задача. Плоская деформация. Функция напряжений Эри. Концентрация напряжений в окрестности полостей.

Цель лекций: Исследовать влияние концентрации напряжений на прочность. Ключевые слова: метод сил; функция напряжений; бигармонические уравнения;

концентрация напряжений.

Основные вопросы (положения) и краткое содержание:

В этих лекционных занятиях будут рассматриваться следующие основные понятия и положения МДТТ: вводиться функция напряжений для определения компонентов тензора напряжений; дается определение плоской деформаций и плоского напряженного состояния; будет доказано, что концентрация напряжения не зависит от контура выреза.

Основные схемы, формулы и т.д., иллюстрирующее содержание:

Плоская задача теории упругости. Плоская деформация

В задаче о плоской деформации рассматривается частное решение уравнений теории упругости, в которой перемещения:

u = u(x, y), v = v(x, y), w = const.

(5.1)

Очевидным следствием этих предположений является отсутствие напряжений τ zx ,τ zy :

σx =σx (x, y), σy =σy(x, y), σz =σz (x, y), τxy = τxy(x, y), τzx =0, τzy =0.

(5.2)

Обобщенный закон Гука при этих условиях записывается в виде:

∂u

∂v

2μ

= 2μ

− 2v

∂x

1 − 2v

∂y

(5.3)

τ = μ ∂u + ∂v

σ = 2μ

ε ,

∂y

∂x

1 − 2v

здесь

ε1

∂u +

∂v =

1 − 2ν

(σ x + σ y ).

(5.4)

∂x

∂y

2μ

На основании (5.3), (5.4), приведем выражение σ z к виду

σz

= ν(σx + σy ),

5.5)

и этим задача определения σ z отодвигается на второй план, речь идет о разыскании плоского поля напряжений σx , σy , τ xy .

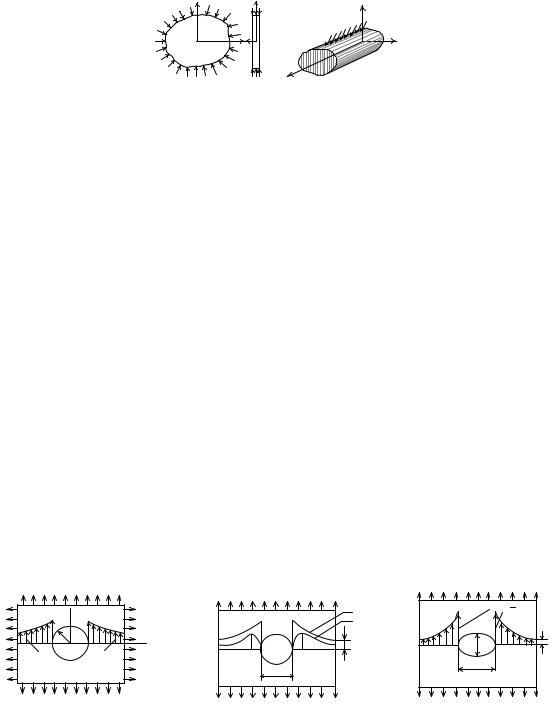
Плоская деформация реализуется в призматическом теле, теоретически бесконечной длины, нагруженном поверхностными и объемными силами, перпендикулярными оси z = x3 , интенсивность которых не зависит от x3 (рис. 6: б).

Тогда все поперечные сечения тела находятся в одинаковых условиях, чем оправдывается задание перемещений в форме (5.1). Приближенно плоская деформация осуществляется в удаленной от торцов средней части тела конечного протяжения по оси z = x3 .

Рис. 6

Уравнения статики плоской задачи в объеме записываются в виде

∂σ	x +		∂τxy		+ F	= 0,
				∂y
∂x					x

∂τyx		+		∂σy	+ F	= 0,
				∂y
∂x					y

ана поверхности, иначе говоря, на контуре Г поперечного сечения тела,

Г: σx nx + τxyny = qx ,

τyx nx + σyny = qy .

Функция напряжений Эри

Рассмотрим однородные уравнения статики:

∂σx	+	∂τxy	= 0,	∂τyx	+	∂σy	= 0.
∂x		∂y		∂x		∂y

(5.6)

(5.7)

(5.8)

Каждое по отдельности из двух однородных уравнений статики (5.8) тождественно удовлетворяется с функцией Ф(х,у) - функция напряжений Эри (Airy):

σ x

∂ 2 Ф

σ y

∂ 2 Ф

τxy

= −

∂ 2 Ф

(5.9)

∂у2

∂x 2

∂x∂у

Дифференциальное уравнение для функции напряжений

Рис. 7

Рис. 8

Рис. 9

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.11.2019283.14 Кб4Лекции 1-МСФО 32 и 39-Первонач.признание.doc
#
22.11.2019175.23 Кб6Лекции 2_МСФО 32_39_Прекращение признания.docx
#
24.03.2015543 Кб136лекции ИОТ.docx
#
24.03.2015593.92 Кб197Лекции Каирбекова Ж2.doc
#
24.03.2015711.29 Кб50лекции МДТТ каз.pdf
#
24.03.2015722.6 Кб38ЛЕКЦИИ МДТТ РУС.pdf
#
16.11.2019152.69 Кб21ЛЕКЦИИ ПО ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИ1.docx
#
24.03.2015165.68 Кб22лекции по ИНФ.docx
#
24.09.2019374.27 Кб51Лекции по макре.doc
#
13.11.2019868.86 Кб21Лекции по микробиологии.doc
#
08.03.2016117.93 Кб81Лекции по Пс-пед конс.docx