
лекции МДТТ каз
.pdf4. 4 - Бөлім Дəрістердің қысқаша мазмұны
№1-2 дəрісі.
Тақырыптың аты: Мор диаграммасы. Кернеулер ар ындылығы. Деформацияларар ындылығы. Кернеу девиаторы. Деформация девиаторы.
Дəрістің мақсаты: Мор диаграммалары жайында мəлімет беру. Жалпыланған кернеулер мен деформациялар жайында мəлімет беру. Кернеуленген к йлерді геометриялы сипаттауын беру.
Түйінсөздер: Мор диаграммасы; кернеу ар ындылығы; деформацияларар ындылығы; кернеу девиаторы; деформация девиаторы.
Негізгі сұрақтар (ұғымдар) жəне қысқаша мазмұны:
Бұл дəрістік сабақтарда ДҚДМ негізгі ұғымдары беріледі: кернеуленген күй; бас кернеулер; бас алаңдар; бас жанама кернеулер; гидростатикалық қысым; кернеу девиаторы; кернеу тензорының инварианттары; бас деформациялар; деформация девиаторы; деформация девиаторының инварианттары; деформациялар қарқындылығы; кернеу қарқындылығы; Мор диаграммасы; Кернеуленген күйлердің геометриялық сипаттауы.
Мазмұнын сипаттайтын негізгі схемалар, формулалар жəне б.қ., :
Кернеуленген к й
Тұтас ортаның кез-келген нүктесіндегі кернеуленген күйі симметриялық кернеу тензорымен сипатталады
|
σ x |
τ xy |
|
|
|
τ xz |
|
||
σˆ = τ xy |
σ y |
τ yz , |
(1.1) |
|
|
|
τ yz |
|
|
τ xz |
σ z |
|
||
м ндағы x,y,z – |
декарт координаттар ж йесі, σx , σy ,σz – |
нормаль кернеулер, |
|
τxy , τyz , τxz – жанама кернеулер. |
|
|
R |
|
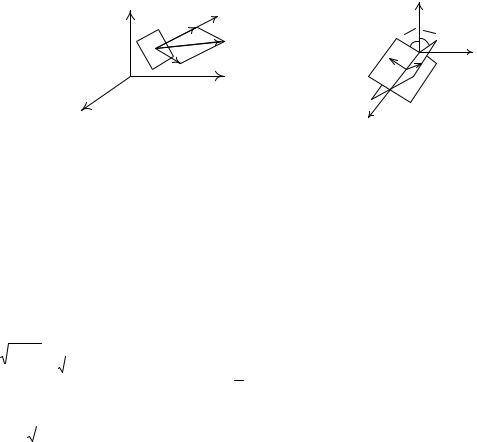
Кернеу векторы |
pп (1-Сурет) Коши формуласымен анықталады: |
|
px = σx n x + τxy n y + τxz nz , |
|
|
|
= τxy nx + σyn y + τyz nz , |
(1.2) |
py |
||
|
= τxz n x + τyz n y + σz nz , |
|
pz |
|
|
|
nx = cos(n, x), n y = cos(n, y), nz = cos(n, z) – бірлік нормаль вектордың |
R |
мұндағы |
n |
құраушылары. Нормаль кернеу σn жəне жанама кернеу τn шамаларын анықтайтын формулалар:
σ n = σ x nx2 + σ y ny2 |
+ σ z nz2 + 2τ xy nx ny + 2τ yz ny nz + 2τ zx nz nx ; |
(1.3) |
|||||||
τn = (p2x + p2y + pz2 − σn2 )1/ 2 . |
|
|
|
|
|
||||
(1.4) |
|
|
|
|
нормаль кернеулерін σ1, σ2 , σ3 |
|
|||
Кернеу тензорының үш бас |
таңбасы арқылы |
||||||||
белгілейміз |
|
σ1 > σ2 > σ3 . |
|
|
|
|
|
||
|
|
|
|
|
|
(1.5) |
|||
Кернеу тензорының үш бас жанама кернеулерінің τ1 , τ2 , τ3 шамаларын (1.2)-(1.4) |
|||||||||
формулаларын пайдалана отырып табуға болады (2-Сурет): |
|
||||||||
τ = σ2 − σ3 , |
τ |
2 |
= σ3 − σ1 , |
τ |
3 |
= σ1 − σ2 . |
( 1.6) |
||
1 |
2 |
|
2 |
|
|
2 |
|
||
|
|
|
|
|
|
|
|||
Жанама кернеудің ең үлкен мəнін (1.5)-(1.6) табамыз: |
|
||||||||
|
|
τmax |
= −τ2 = σ1 − σ3 . |
|
|
||||
|
|
|
|
|
2 |
|
|
|
|
Z |
|
n |
|
|
|
|
|
N |
|
|
ρ |
|
м |
N |
|
|
|
0 |
|
N |
|
|
|
|
|
Y |
X |
|
|
|
|
|
|
|
|
1-Сурет |
|
|
|
2-Сурет |
||
Кернеу тензорының үш бас инварианттары бар: |
|
||||||
Ι1 (σˆ ) = σ 1 + σ 2 + σ 3 ≡ 3σ , |
|
||||||
|
Ι 2 |
(σˆ ) = −(σ 1σ 2 + σ 2σ 3 + σ 3σ 1 ), |
(1.7) |
||||
|
|||||||
Ι |
3 |
(σˆ ) = σ σ |
σ |
3 |
, |
|
|
|
|
1 2 |
|
|
|
||
мұндағы
|
|
|
|
|
|
|
σ = |
1 |
(σx + σy + σz ), |
(1.8) |
|
|
|
|
|||||||
|
|
|
3 |
|
|
|||||
орташа (немесе гидростатикалы ) кернеу ( ысым) деп аталады. |
|
|||||||||
|
Нүктедегі жанама кернеулер ар ындылығы |
|
||||||||
τi |
= + |
Ι2 |
(σˆ 2 ) |
= |
1 |
[(σ −σ )2 +(σ −σ )2 +(σ −σ )2 +6(τ2 +τ2 +τ2 )]1/ 2. |
(1.9) |
|||
|
|
|||||||||
|
|
x y y z z x xy yz xz |
|
|||||||
|
|
|
6 |
|
|
|
|
|||
Кернеулер қарқындылығы (σi = 
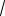 3τi )
3τi )
σ = |
1 |
|
[(σ − σ )2 + (σ − σ )2 + (σ − σ )2 ] 1 / 2. |
(1.10) |
|
|
|
||||
i |
|
1 2 2 3 3 1 |
|
||
2 |
|
|
|
||
Мор диаграммасы. Берілген нүктедегі координаттар жүйесінің бағыттары бас |
|||||
бағыттар болсын деп алайық. Кернеу векторының компоненттерінің |
σn мен τn |
||||
мəндері алдын ала берілді деп есептеп, олардың қандай алаңға сəйкес екендігін табу керек.
Үш |
|
белгісіздерді |
|
n12 , n22 , n32 |
|
(1.2)-(1.4) формулаларын |
пайдаланып табамыз |
|||||||||||||||||||
(n12 + n22 + n32 = 1): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n2 = |
|
|
f1(σn,τn ) |
|
, |
|
|
n2 = |
|
|
f2(σn,τn ) |
|
|
, |
|
|
|
|
||||||||
(σ1 |
−σ2 )(σ1 −σ3) |
|
|
(σ2 −σ1)(σ2 −σ3) |
|
|
|
|
||||||||||||||||||
1 |
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
f3(σn,τn ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.11) |
||||
|
|
|
n2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
(σ3 |
−σ1)(σ3 −σ2 ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мұндағы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (σ |
|
, τ |
|
) = τ2 |
|
|
|
− |
σ |
|
|
+ σ |
|
2 |
− |
|
σ |
|
− σ |
|
2 |
|
||||
|
|
+ σ |
|
|
2 |
|
2 |
3 |
|
|
|
2 |
|
|
3 |
, |
|
|||||||||
1 |
|
n |
|
n |
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||
f2 (σn |
, τn ) = τn2 + |
|
σn |
− |
σ |
|
|
+ σ |
2 |
− |
|
σ |
|
− σ |
|
2 |
(1.12) |
|||||||||
|
|
3 |
2 |
1 |
|
|
|
3 |
2 |
1 |
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f3 (σn |
|
|
|
|
|
σn |
− |
σ + σ |
|
2 |
− |
|
σ − σ |
|
|
2 |
|
|||||||||
, τn ) = τn2 + |
|
1 |
|
2 |
2 |
|
|
1 |
2 |
2 |
. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Есептің |
шешімін |
(1.5) шартын ескере отырып, |
(1.11)-(1.12) табамыз: |
|
f1 > 0, |
f2 < 0, |
f3 > 0, |
(1.13) |
|
σn , τn мəндері |
үш |
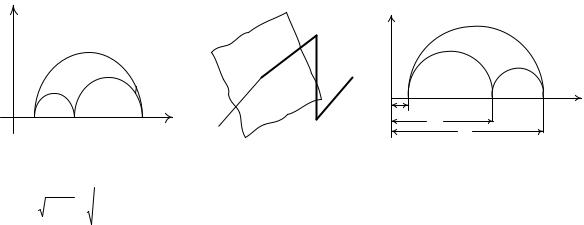
шеңберлермен шектелген аймақта жатады |
(3-Сурет). Бұл жердегі |
|
σ 1 ,σ 2 ,σ 3 |
- бас кернеулер (4-Сурет). |
|
||
Деформация
Тұтас ортаның деформациясы симметриялық деформация тензорымен сипатталады:
|
|
ε |
|
|
1 |
γ |
|
|
1 |
γ |
|
|
|
|||
|
|
x |
|
|
xy |
|
xz |
|
|
|||||||
|
|
2 |
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
εˆ = |
|
1 |
|
γ |
|
ε |
|
|
|
1 |
γ |
|
|
(1.14) |
||
|
|
|
|
|
|
|
|
|
, |
|||||||
2 |
|
|
|
|
2 |
|
||||||||||
|
|
|
|
xy |
|
|
y |
|
|
|
yz |
|
||||
|
|
1 |
|
γ xz |
1 |
γ yz |
ε z |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||
|
2 |
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
мұндағы εx , εy ,εz – салыстырмалы зару, γxy , γ yz , γzx – салыстырмалы ығысу. Деформация тензорының үш бас заруын ε1, ε2 , ε3 таңбасымен белгілейміз (5-Сурет). Үш бас ығысуды мына формуламен анықтаймыз
γ1 = ε2 − ε3 , γ2 |
|
= ε3 − ε1, γ3 |
= ε1 |
− ε2 . |
(1.15) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3-Сурет |
|
|
4-Сурет |
|
5-Сурет |
|||||||
Ығысу деформацияларының қарқындылығы |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γi |
=+2 |
Ι2(εˆ2) |
= |
|
2 |
|
(εx −εy )2 |
+(εy −εz )2 |
+(εz |
−εx )2 + |
3 |
(γxy2 +γyz2 |
+γzx2 ) . |
(1.16) |
|
|
|||||||||||||
|
|
|
|
|
3 |
|
|
2 |
|
|
||||
Өзін тексеру үшін сұрақтар:
1. Кернеу векторы деген не? 2. Мор диаграммасы не үшін керек? 3. Кернеу жəне деформация қарқындылықтары ұғымы не үшін кіргізіледі?
Ұсынатын əдебиет:
1.Работнов Ю.Н. Механика деформируемого твердого тела.- М.: Наука, 1988. - 712 с.
2.Искакбаев А. Деформацияланатын қатты дене механикасының негіздері. - Алматы: Изд- во Қазақ университетi, 2007. -176 бет.
№ 3-4 дəрісі.
Тақырыптың аты: Деформацияларды йлесімділігіні тензорлы шарты (Сен-
Венан). Серпімді ортаны сызы ты моделі. Ламе т ра тылары. Серпімді ортаны техникалы т ра тылары. Гук за дары. Беріктікті классикалы теориясы.
Дəрістің мақсаты: Классикалык беріктік теориясыны негізін беру.
Түйінсөздер: Ламе т ра тылары; Гук за дары; йлесімділік шарты; беріктік шегі; а ыштык шегі; потенциалдык энергия.
Негізгі сұрақтар (ұғымдар) жəне қысқаша мазмұны:
Бұл дəрістік сабақтарда ДҚДМ негізгі ұғымдары беріледі: Сен-Венанның шарты; серпімді ортаның сызықты моделі; беріктік теориясының негізгі болжамдары; Ламе тұрақтылары; серпімді ортаның техникалық тұрақтылары; Гук заңдары.
Мазмұнын сипаттайтын негізгі схемалар, формулалар жəне б.қ., :
Сен-Венанны тензорлы шарты:
) |
(2.1) |
rot(rot ε)* = 0 , |
м ндағы ε) – симметриялы деформация тензоры, ал (*) – орыналмастыру та басы.
Серпімді денені сызы ты моделі
Біртекті изотропты дененің серпімді қасиетін сипаттайтын Гук заңының тензорлық теңдеуін мына түрде жазамыз:
ˆ |
ε + 2μ εˆ , |
(2.2) |
||
σˆ = λ E |
||||
ˆ |
ε – салыстырмалы к'лемдік деформация, λ,μ – |
Ламе |
||
м ндағы E – бірлік тензор, |
||||
параметрлері (денені меха-никалы асиетін сипаттайтын математикалы |
||||
т ра ты шамалар). Гук за ын (2.2) екі т рге т рлендіреміз: |
|
|||
σ = K ε , |
(2.3) |
|||
σˆ 2 = 2μ εˆ 2 , |
(2.4) |
|||
м ндағы σ – орташа кернеу, |
ε – к'лемдік деформация, σˆ 2 – кернеу девиаторы, εˆ 2 – |
|||
деформация девиаторы, К – серпімділіктің көлемдік модулі |
|
|||
K = λ + |
2 |
μ. |
(2.5) |
|
|
||||
|
3 |
|
|
|
Меншікті потенциалды энергия. Серпімділік потенциал |
|
|||
Берілген н ктені ма айындағы бірлік к'лемде дефор-мация процесі кезінде |
||||
жина талатын энергияны – |
серпімді денені меншікті потенциалдық энергиясы деп |
|||
атайды. Сызы ты серпімді денені меншікті потенциалды энергиясын мына фор- муламен сипаттаймыз:
U = |
1 |
ˆ |
ˆ |
(2.6) |
|
||||
2 |
σ × ×ε , |
|||
м ндағы σˆ – кернеу тензоры, εˆ |
– деформация тензоры, ал (··) – |
екі рет скаляр |
||
к'бейту та басы.
Беріктіктің классикалық теориялары. Ең үлкен нормаль кернеулер теориясы
Б л теорияны негізін Галилей болжамы райды: егер е лкен нормаль кернеулер, кернеуленген к йлер т ріне тəуелсіз, берілген шектік мəнінен асып кетсе
беріктік б зылады. |
|
.ауіпті к йді аны тайтын шарт |
|
σ1 = (σ )+ немесе σ3 = (σ )- , |
(2.7) |
м ндағы (σ )+ мен (σ )- лгіні созылу жəне сығылу жағдайы шін ауіпті кернеулер.
Е лкен сызы ты деформациялар теориясы
Бұл теорияның негізін Мариотта болжамы құрайды: егер абсолюттік шамасы ең үлкен салыстырмалы сызықты деформация, кернеуленген күйлер түріне тəуелсіз, берілген шектік мəнінен асып кетсе беріктік бұзылады.
Гук заңын ескере отырып, қауіпті күй шартын былай жазамыз
εmax E = [σ1 − ν(σ2 + σ3 )] = σb + ,
εmin E = [σ3 − ν(σ1 + σ2 )] = σb −
немесе |
σ − ν(σ |
|
+ σ |
) = σ |
|
|
|
σэкв |
|
b + |
, |
|
|||
= 1 |
2 |
3 |
|
|
(2.8) |
||
|
σ3 − ν(σ1 |
+ σ2 ) = σb − , |
|
||||
м ндағы σэкв |
– ар ылы кернеу баламалығы белгіленді, σ b – |
лгіні беріктік шегі |
|||||
(шартты кернеуді е лкен мəні – максималь кернеу).
Е лкен жанама кернеулер теориясы
Бұл теорияның негізін Кулон-Треск болжамы құрайды: егер ең үлкен жанама кернеулер, кернеуленген күйлер түріне тəуелсіз, берілген шектік мəнінен асып кетсе беріктік бұзылады.
Қауіпті күйді анықтайтын шарт
tmax = τқ= tT
мұндағы tT – үлгінің аққыштық шегі.
Толы потенциалды энергия теориясы
Бұл теорияның негізін Бельтрами болжамы құрайды: егер деформацияның меншікті потенциалдық энергиясы, кернеуленген күйлер түріне тəуелсіз, берілген шектік мəнінен асып кетсе беріктік бұзылады. Бельтрами критерийі іс жүзінде пайдаланбайды (қолданбайды).
Пішін 'згерту энергия теориясы
Бұл теорияның негізін Губер болжамы құрайды: егер пішін өзгерту меншікті потенциалдық энергиясы, кернеуленген күйлер түріне тəуелсіз, берілген шектік мəнінен асып кетсе беріктік бұзылады.
Өзін тексеру үшін сұрақтар:
1. Изотропты сызықты серпімді ортаны сипаттау үшін қанша тұрақты керек? 2. Бельтрам гипотезасы іс жүзінде неге пайдаланбайды ?
Ұсынатын əдебиет:
1.Работнов Ю.Н. Механика деформируемого твердого тела.- М.: Наука, 1988. - 712 с.
2.Искакбаев А. Деформацияланатын қатты дене механикасының негіздері. - Алматы: Изд- во Қазақ университетi, 2007. -176 бет.
№ 5 - 6 дəрісі.
Тақырыптың аты: Сызы ты серпімділік теориясыны негізгі атынастары.
Шектік есептер. Шешу əдістері. Орын ауыстыру əдісі. Навье - Коши дифференциалды те деулері.
Дəрістің мақсаты: Изотропты біртекті серпімді ортаны сипаттайтын те деулерді орытып шығару.
Түйінсөздер: серпімділік за дары; Коши атынастары; т тас ортаны озғалыс те деулері.
Негізгі сұрақтар (ұғымдар) жəне қысқаша мазмұны:
Бұл дəрістік сабақтарда ДҚДМ негізгі ұғымдары беріледі: сызықты серпімділік теориясының негізгі қатынастары; шектік есептер; шешу жолдары; орын ауыстыру əдістері; Навье - Коши дифференциалдық теңдеулері.
Мазмұнын сипаттайтын негізгі схемалар, формулалар жəне б.қ., :
Сызы ты серпімділік теориясыны негізгі атынастары - Сызы ты серпімділік теориясыны негізгі те деулері
Ол теңдеулер үш топ қатынастары арқылы беріледі.
Бірінші топ – тепе-теңдіктің векторлық теңдеуі
R |
= 0 , |
|
ˆ |
(3.1) |
|
divσ + F |
мұндағы σˆ кернеу тензоры R көлемдік күштің векторы
– , F – .
Екінші топ – геометриялық қатынастарды сипаттайтын тензорлық теңдеуі:
|
ˆ |
1 |
|
R |
R |
* |
|
|
ε = |
|
[Ñu |
+ (Ñu ) |
], |
(3.2) |
|
|
2 |
||||||
|
|
|
|
|
|
|
|
€ |
деформацияның сызықты тензоры, Ñ – |
набла-операторы, u – орын |
|||||
мұндағы e – |
|||||||
|
|
|
|
|
|
|
R |
ауыстыру векторы, ал (*) – |
орыналмастыру таңбасы. |
|
|||||
6шінші топ – сызықты серпімді дененің күй заңы. Изотропты дене үшін (изотермиялық немесе адиабаттық процесс кезінде) жалпыланған Гук заңын мына түрлерде жазуға болады:

|
|
|
ν |
|
ˆ |
|
|
|
ˆ |
|
|
|
|
ˆ |
(3.3) |
||
|
|
|
|
|||||
σ = 2μ |
1- 2ν εE + ε |
, |
||||||
ˆ |
1 |
|
ˆ |
3ν |
ˆ |
|
|
|
2μ |
|
1+ν σE |
|
(3.4) |
||||
ε = |
|
σ - |
, |
|||||
мұндағы μ = G -ығысу модулі, ν -Пуассон коэффициенті, ε -салыстырмалы көлемдік
деформация σ гидростатикалық қысым ˆ бірлік тензор
, - , E - .
Симметриялық екінші рангалы екі тензордың σˆ εˆ он екі құраушылары мен R
, u
векторының үш құраушыларын он бес теңдеуден (3.1-3.3) табуға болады.
Шеттік шарттар
Жоғарыда келтірілген теңдеулер жүйесі (3.1-3.3) сызықты серпімді дененің көлемінің (V) ішіндегі нүктелердегі күйін сипаттайды. Бұл теңдеулерге дененің бетінде
(S) қойылатын шарттар қосылады. Серпімділік теориясында үш түрлі шеттік есептер қарастырылады.
Бірінші шеттік есеп – кинематикалы шеттік шарт:
R |
|
|
R |
|
|
|
u |
|
S |
= u* |
(x1, x2 |
, x3 ), |
(3.5) |
|
|
мұндағы u -орын ауыстыру векторы (V-көлемінде іздестіріледі), ал u* -орын ауыстыру |
|
R |
R |
векторының берілген мəні. Бұл шарттағы (3.5) x1, x 2 , x3 – координаттары бет (S) теңдеуімен байланысты.
Екінші шеттік есеп – статикалы есеп.
Бұл жағдай үшін шеттік шарт:
|
R |
ˆ |
R |
|
|
|
(3.6) |
|
n |
×σ |
S = q, |
|
|
|
|
R |
|
|
|
|
|
R |
|
|
|
|
|
|
|
||
мұндағы n дене бетінің сыртқы нормалының бірлік векторы, ал q – үлестірілген беттік |
|||||||
күштің берілген мəні. |
|
|
|
|
|
|
|
6шінші шеттік есеп – |
аралас есеп. Беттің бір бөлігінде S1 кинематикалық |
||||||
шеттік шарт (3.5), ал екінші бөлігінде S2 – |
статикалық шеттік шарт (3.6) қойылады: |
||||||
R |
|
R |
R |
ˆ |
|
R |
|
u |
= u* |
(x1 , x2 , x3 ), n |
×σ |
|
= q. |
(3.7) |
|
|
S1 |
|
|
|
S2 |
|
|
Серпімділік теориясыны есептерін шешуді екі тəсілі бар. Бірінші тəсіл |
|||||||
бойынша алдымен орын ауыстыру векторын u |
іздестіреді, сонан кейін ол арқылы (3.2) |
||||||
|
|
|
|
|
R |
|
|
формуласын пайдалана отырып деформация тензорын εˆ жəне Гук заңы (3.3) арқылы кернеу тензорын σˆ табады. Екінші тəсіл бойынша деформация тензоры εˆ дененің тұтастық шартын қанағаттандыратын күйге сəйкес келетін кернеу тензорын σˆ
іздестіреді Орын ауыстыру векторын R Чезаро формуласы арқылы табады
. u .
Орын ауыстырулар ар ылы 'рнектелген серпімділік теориясыны дифференциалды те деулері
Орын ауыстыру векторы R арқылы дифференциалдық теңдеуді қорытып шығару u
үшін, (3.2-3.3) теңдеуін статикалық теңдеуге (3.1) қоямыз
μdiv 2ν
1- 2ν
енді операторларды есептей отырып
εE + Ñu + (Ñu ) |
+ F = 0, |
||
ˆ |
R |
R * |
R |
R |
|
ˆ |
|
ˆ |
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
ε = divu , |
divεE = E × gradε = draddiv u, |
|
|
|
|
|
|
|
|||||||||||||
R |
|
R |
= Ñ |
R |
Ñ2 |
- Лаплас операторы , |
|
|
|
||||||||||||
divÑu = Ñ ×Ñu |
2u , |
|
|
|
|||||||||||||||||
R * |
|
|
|
R * |
R |
¶ |
|
R R |
¶u |
|
|
R |
¶2u |
S |
R |
|
|
|
|||
div(Ñu ) = Ñ × (Ñu ) |
= e |
|
|
|
×e e |
|
|
k |
= e |
|
= graddiv u, |
|
|
|
|||||||
|
|
|
¶x |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
S ¶x |
S |
k t |
t |
¶x ¶x |
S |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
t |
|
|
|
|
||||
мына іздеген дифференциалдық теңдеуге келеміз |
|
|
|
||||||||||||||||||
|
1 |
|
|
|
|
R |
|
R |
|
1 |
|
R |
|
|
|
|
|
|
|
||
|
|
|
|
graddiv u+ Ñ2 u+ |
|
|
|
F = 0 . |
|
|
|
|
|
|
|||||||
|
1 - 2n |
m |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ μÑ2 |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
R |
+ F |
|
Навье - Коши- Ламе озғалыс те деулері: (λ + μ )graddiv u |
u |
||||||||||||||||||||
Векторлы |
|
атынас: rotrot u = graddiv u - Ñ2u . |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
R |
|
R |
|
|
|
||
Векторлы |
|
|
|
|
R |
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
||
|
атынас: u |
= Ñϕ + rotψ . |
|
|
|
|
|
|
|
||||||||||||
(3.8)
¶2 R
=ρ ¶tu2 .
Өзін тексеру үшін сұрақтар:
1. Орын ауыстыру əдісі кезінде Сен-Венан шарттарын тексеру керекпе? 2. Сызықты серпімді теорияның есептерінде суперпозиция принципін пайдалануға болама?
Ұсынатын əдебиет:
1.Работнов Ю.Н. Механика деформируемого твердого тела.- М.: Наука, 1988. - 712 с.
2.Искакбаев А. Деформацияланатын қатты дене механикасының негіздері. - Алматы: Изд- во Қазақ университетi, 2007. -176 бет.
№ 7 - 8 дəрісі.
Тақырыптың аты: К ш əдісі. Бельтрами-Мичеллді тензорлы тендеуі. Клапейрон
формуласы. Кирхгоф теоремасы.
Дəрістің мақсаты: Сызы ты серпімді теорияны шектік есептеріні шешіміні жалғыздығын дəлелдеу.
Түйінсөздер: Сен-Венан шарттары; к ш əдісі; Бельтрами-Мичелл шарттары.
Негізгі сұрақтар (ұғымдар) жəне қысқаша мазмұны:
Бұл дəрістік сабақтарда ДҚДМ негізгі ұғымдары беріледі: күш əдісі; Бельтрами- Мичеллдің тензорлық тендеуі; Клапейрон формуласы; Кирхгоф теоремасын дəлелдеу.
Мазмұнын сипаттайтын негізгі схемалар, формулалар жəне б.қ., :
Кернеулер ар ылы шешім. Бельтрами-Мичелл те деулері
Гуктың көлемнің серпімді өзгеру заңын ескере отырып, мына қатынасқа келеміз
Ñ2σ = 0. |
(4.1) |
Статиканың тепе-теңдік теңдеулерін көлем ішінде қанағаттандыратын кернеу тензоры σˆ ішінен, сол арқылы есептелген εˆ Сен-Венанның үйлесімділік шартын қанағаттандыратын бөлігін таңдап алуымыз керек:
ˆ |
= rot(rotε ) |
* |
= |
1 |
Ink |
|
ˆ |
3ν |
ˆ |
|
= 0, |
(4.2) |
|
|
|
|
|||||||||
|
2μ |
|
||||||||||
Inkε |
|
|
σ - |
1 +ν σE |
|
|||||||
мұндағы Ink ( йлесімсіздік)-симметриялық екінші рангалы тензор. Статиканың теңдеулерін пайдалана отырып, (4.1) теңдеуін ескере келе, (4.2) тензорлық теңдеуінен Бельтрами-Мичелл шартын (4.3) қорытып шығарамыз
2 |
ˆ |
3 |
ÑÑσ = 0. |
|
|
Ñ |
1+ν |
(4.3) |
|||
σ + |
Декарт координаталар жүйесінің құраушылары арқылы мына түрде жазылады:
Ñ2sx |
+ |
|
|
|
3 ¶2s |
= 0, |
Ñ2txy |
+ |
|
|
|
3 |
|
¶2s |
= 0, |
|
|||
|
|
|
|
|
|
|
|
|
|||||||||||
|
+ n ¶x2 |
|
|
|
|
|
|
||||||||||||
|
1 |
|
|
1 |
+ n ¶x¶y |
|
|||||||||||||
Ñ2sy |
+ |
|
|
|
3 ¶2s |
= 0, |
Ñ2tyz |
+ |
|
|
|
3 |
|
¶2s |
= 0, |
(4.4) |
|||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
+ n ¶y2 |
|
|
|
|
|
||||||||||||
|
1 |
|
|
1 |
+ n ¶y¶z |
|
|||||||||||||
Ñ2sz |
+ |
|
|
|
3 ¶2s |
= 0, |
Ñ2tzx |
+ |
|
|
|
3 |
|
¶2s |
= 0. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
+ n ¶z2 |
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
1 |
+ n ¶z¶x |
|
|||||||||||||
Клапейрон формуласы. Кирхгоф теоремасы
~
Серпімді дененің деформациясының потенциалдық энергиясын U меншікті потенциалдық энергия U бойынша былай анықтауға болады:
~ |
|
U = ∫ Udv. |
(4.5) |
V
Енді мына тепе-теңдікті жазайық (4.6):
|
ˆ |
R |
|
ˆ |
|
|
R |
R |
R |
R |
|
||
∫ u |
× (divσ + F )dv + ∫ (q |
- n |
×σ ) × uds = 0. |
(4.6) |
||
V |
|
S |
|
|
|
|
Тензорлық анализдің вектордың дивергенциясын есептейтін формуласын еске түсірейік:
div(u ×σ ) = u ×divσ +σ ××ε . |
(4.7) |
|||
R ˆ |
R |
ˆ ˆ |
ˆ |
|
Серпімді деформацияның меншікті потенциалдық энергиясының анықтамасын ескеріп жəне (4.7) қатынасын пайдаланып төмендегі түрлендіруді жасаймыз:
∫ u × divσdv = ∫ div(u ×σ )dv - ∫ σ × ×εdv = |
|||||
R |
ˆ |
R |
ˆ |
ˆ |
ˆ |
|
|
|
|
||
V |
ˆ |
V |
|
V |
|
R |
R |
|
|
|
|
= ∫ n |
×σ × uds - ∫ 2Udv. |
|
|
||
S |
|
V |
|
|
|
Енді (4.8) апарып (4.6) қоямыз
~ 1 |
|
R R |
R R |
|
|
U = |
|
|
|
|
|
2 |
|
∫ F × udv + ∫ q × uds , |
|||
|
V |
S |
|
||
~
мұндағы U -серпімді деформацияның потенциалдық энергиясы (4.5).
Кирхгоф теоремасы.
Егер төмендегі үш шарттар:
(4.8)
(4.9)
1)дененің бастапқы күйі – табиғи күй;
2)дененің əрбір нүктесінде деформацияның меншікті потен-циалдық энергиясы шартын қанағаттандырады;
3)деформация тензоры мен осьтік айналу векторы ωR құраушылары(4.10) шартын қанағаттандырады
eij |
<< 1, |
|
wk |
|
<< 1 ; |
(4.10) |
|
|
|||||
|
|
|
|
|
|
|
орындалатын болса, онда сызықты серпімділік теориясының шеттік есептерінің шешімі жалғыз болады.
Өзін тексеру үшін сұрақтар:
1. Қай кезде Бельтрами-Мичелл шарттарын пайдалану қажет? 2. Қандай шарттар үшін Кирхгоф теоремасын пайдалануға болмайды?
Ұсынатын əдебиет:
1.Работнов Ю.Н. Механика деформируемого твердого тела.- М.: Наука, 1988. - 712 с.
2.Искакбаев А. Деформацияланатын қатты дене механикасының негіздері. - Алматы: Изд- во Қазақ университетi, 2007. -176 бет.
№ 9 - 10 дəрісі.
Тақырыптың аты: Жазы есеп. Эриді кернеу функциясы. уыстарды ма айындағы кернеулер шоғырлануы.
Дəрістің мақсаты: Кернеулер шоғырлануыны беріктікке əсерін зерттеу. Түйінсөздер: к ш əдісі; кернеу функциясы; бигармоникалык те деу; кернеу
шоғырлануы.
Негізгі сұрақтар (ұғымдар) жəне қысқаша мазмұны:
Бұл дəрістік сабақтарда ДҚДМ негізгі ұғымдары беріледі: кернеу тензорының компоненттерін анықтау үшін кернеу функциясын кіргізу; жазық деформация жəне жазық кернеуленген күйдің анықтамасы беріледі; кернеу шоғырлануы қуыстың жиегінен тəуелсіз екені дəлелденеді.
Мазмұнын сипаттайтын негізгі схемалар, формулалар жəне б.қ., :
Жазы деформация. Бұл жағдайда серпімділік теориясының мына түрдегі дербес шешімін қарастырады:
|
|
|
u = u(x, y), |
v = v(x, y), |
|
|
|
w = const. |
|
(5.1) |
||||||||||||||||
Мұндай шешімнің (5.1) салдарынан: |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
σx = σx (x,y), |
σy = σy (x,y), σz = σz (x,y), |
(5.2) |
|||||||||||||||||||
|
|
|
|
|
τxy = τxy(x, y), τzx = 0, |
τzy = 0. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Енді (5.1)- (5.2) ескере отырып, Гук заңын мына түрде жазуға болады: |
|
|||||||||||||||||||||||
|
|
|
|
v |
|
|
|
|
∂u |
|
|
|
|
|
|
|
|
v |
|
|
|
∂v |
|
|||
σ |
x |
= 2μ |
|
|
|
|
ε |
1 |
+ |
|
, |
σ |
y |
|
= 2μ |
|
|
ε |
1 |
+ |
, |
|
||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
1 − 2v |
|
∂x |
|
|
|
|
|
|
1 − 2v |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
(5.3) |
||||||||||
|
|
|
∂u |
|
∂v |
|
|
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|||
τ xy |
+ |
|
σ z = 2μ |
|
|
|
|
|
ε1 , |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
= μ |
∂y |
|
|
, |
|
1 |
− 2v |
|
|
|
|
|
||||||||||||||
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
мұндағы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
ε1 |
= |
∂u |
+ |
∂v |
= |
1 − 2ν |
(σ x + σ y ). |
|
(5.4) |
|||||||||||
|
|
|
|
|
|
∂x |
∂y |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2μ |
|
|
|
|
|
|
|
|
|
||
Жазық деформация жағдайында: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
σz |
= ν(σx + σy ), |
|
|
|
|
(5.5) |
|||||||||
сондықтан алдымен σx , σy , τxy кернеулерін іздестіру керек.
Жазық деформация іс жүзінде x 3 = z осі бойында өте үлкен ұзындығы болатын
цилиндрлік (призматикалық) денеде іске асады (6 -Сурет,б). Көлемдік жəне беттік күштер z-осі бойынша бірқалыпты үлестірілген жəне сол оське перпендику-ляр болып келеді (6 -Сурет,б).

6 - Сурет
Серпімділік теориясының жазық есебінің дененің көлеміндегі жəне бетіндегі (дененің көлденең қимасының жиегінде: Г) тепе-теңдік теңдеулері мына түрде жазылады:
¶σ |
x |
+ |
¶τ xy |
+ F |
|
= 0, |
¶τ yx |
+ |
|
¶σ y |
+ F |
|
= 0, |
(5.6) |
¶x |
¶y |
x |
¶x |
|
¶y |
y |
||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Г : σ x nx |
+τ xy ny = qx , |
τ yx nx |
+ σ y ny = q y . |
(5.7) |
||||||||||
Эриді кернеулер функциясы. Статиканың біртекті теңдеулерін (5.6) қарастырайық:
¶s |
x + |
∂τxy |
= 0, |
∂τyx |
+ |
∂σy |
= 0. |
(5.8) |
|
¶y |
¶x |
¶y |
|||||
¶x |
|
|
|
|
||||
Бұл жүйенің (5.8) шешімін табу үшін, жаңадан Ф(х,у) функциясын – Эридің кернеулер функциясын, енгіземіз:
sx = ¶2 Ф , |
sy = ¶2 Ф , |
txy = - |
¶2 Ф |
. |
(5.9) |
||
|
|||||||
¶у2 |
|
¶x 2 |
|
¶x¶у |
|
||
Бұл шешім статиканың біртекті теңдеулерін қанағаттандырады. |
|
||||||
Кернеулер функциясы шін дифференциалды те деу. Жазық деформация |
|
||||||
жағдайында орташа кернеу үшін |
|
|
|
|
|||
|
s = |
1 + n |
Ñ2Ф. |
|
|
|
(5.10) |
|
|
|
|
|
|||
|
3 |
|
|
|
|
|
|
Эри функциясы Бельтрами-Мичеллдің тензорлық теңдеуін қанағаттандыру керек.
Ñ2Ñ2Ф = 0 . |
(5.11) |
уыстарды ма айындағы кернеулерді шоғырлануы. Д гелек уысты жазы ты ты жан-жа ты бір алыпты созу (7 – сурет). Д гелек уысты жазы ты ты бір осьтік созу (Кирш есебі) (8-сурет). Эллипс уысты жазы ты ты бір осьтік созу (колосов-инглис есебі) (9-сурет). !рт"рлі жиекті уысты жазы ты ты бір осьтік созу (10-сурет).
7 - сурет |
8 - сурет |
