Лекции по дифференциальной геометрии §1. Вектор-функция одного скалярного аргумента

З

i

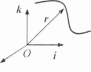
ададим в трехмерном евкли­довом пространстве Е₃ прямо­угольную декартову систему координат R= (О, *,у, к). Пусть каждому действительному числу t из промежутка \а,Ь] поставлен в соответствие век­тор r = г (г), отложенный от начала координат. Тогда бу­дем говорить, что на [с/, /7]

задана вектор-функция от одного скалярного аргумента t. При каждом / будем иметь вектор г (7), который разлагается по ор­там /, у, к :

r (0= x(t) i + у (I) j +z(t) к (1.1)

'Здесь x(t), у((), z(t) - три скалярные функции от аргумента /, которые называются координатами или компонентами вектор- функции. Задание вектор-функции г (I) равносильно заданию )тих трех скалярных функций.

§2. Предел вектор-функции

Вектор а называется пределом вектор-функции г (!) в точке / = t₀ , если для любого положительного числа 8 >0 най­дется число 5>0 такое, что из неравенства | / - /₀|< 5 следует

неравенство г (t) - а \ < 8.

Обозначается : lim r{t) = а

i-*i_Q

Пусть в ортонормированном репере R= (О, /, /, к) задана вектор-функция

г (t)= x(t) i + y(t) j + z(t) к

Имеет место

Теорема 2.1. Для того, чтобы вектор-функция г = г (/) имела своим пределом вектор а в точке t = to , необходимо и достаточно, чтобы в этой точке имели пределы три ее координа­ты x(i), y(t), z(t). При этом, если

lim x{t) = х₀, lim y(t) = y_Q, lim z(t) = z₀,

i >/„ /->/₀ i->t₀

to a = x0 i + yo j + z₀ k.

Доказательство.

1. Необходимость. Пусть вектор a = Xo i + yo j ⁺ Zq к предел вектор-функции г = г (t) в точке t = t₀ Тогда, по опре­делению предела вектор-функции, для любого £ >0 найдется число 5 >0 такое, что из | t - t₀1 < 5 следует | r (t) - а | <£. Но r (t) -а = {x(t) - х₀, у(t -yo, z(t) - zо},

\r(t)-a\= ^(x{t)-x₀f +{уО)~УоУ +(^z(O-^₀)² <£ •

Если в подкоренном выражении мы отбросим два из трех неот­рицательных слагаемых, неравенство усилится. Таким образом, получим:

|x'(t) - xo < £, y(t) -у₀\ < 8, z(t) - Zo\ < 8.

Следовательно, скалярные функции x(t), y(t), z(t) имеют свои­ми пределами соответственно Хо, у о, z₍₎. Необходимость дока­зана.

2. Достаточность. Пусть в точке t = t₀ функции x(t), y(t), z(t) имеют пределы х₀, yo, z₀ соответственно. Тогда, по определению предела обычной функции, для любого 8 >0 най­дется число 5 >0 такое, что из |t - t0 \ < 8 следует:

£

£

<

3 3 - з

Рассмотрим вектор а = хо i + yo j + z₀ к . По свойству модуля вектора: модуль суммы векторов не превосходит суммы моду­лей, - имеем:

г (t)-a | = I (x(t) -хо) / +(y(t)-yo)j +(z(t)-z₀) к | <

£

< |.\'(t) - Х₀| + |Y(t) - yo| + \z{t) -ZoI < — + — + — = 8. Итак,

££ 1 1

3 3 3

§3. Свойства пределов вектор-функции

1 Тусть а = Л = b(t) - две вектор-функции скалярного аргумента, а Я Я(%) - скалярная функция того же аргумента на промежутке [а, р]. И пусть при t —> t_Q

lim a(t) = a₀ , lim b(t) = b₀ , lim A(/) =

/->/„ ^/_>/() '—Hq

Тогда:

1. Предел суммы двух вектор-функций a(t) и b(t) суще­ствует и равен сумме пределов:

lim (а(0 ± b(t)) = а₀ ± Ь₀

1—>1₀

2. Предел произведения скалярной функции X(t) на век­тор-функцию а(0 существует и равен Я₀ a_Q:

lim X(t) a(t) = Я₀ -а₀

t—>t₀

3. Предел скалярного произведения двух вектор- функций a(tj- b(t) существует и равен скалярному произведению их пределов:

lim a{t) • b(t) = а₀ ■ b_{)

t-*t о

4. Предел векторного произведения двух вектор- функций [a(t)- b(l)] существует и равен векторному произведе­нию их пределов:

\\m[a(t)-b(t)] = [a₀-b₀]

t->t „

Все эти свойства непосредственно следуют из теоремы 2.1

Вектор-функция г = г (!) называется непрерывной в точке t = t„, если lim r{t) = r(t₀).

Теорема 4.1. Вектор-функция г (^= / + y(t) j + z(^ к

непрерывна в точке t = t_Q тогда и только тогда, когда в этой точке непрерывны все ее координаты x(t), y(t), z(t), то есть, lim x{t) = x(t₀), lim y(t) = y{t₀), lim z(t) = z(t₀).

/—>/,1 / —I —И()

Следует непосредственно из теоремы 2.1.