§5. Производная вектор-функции

Вектор-функция г = г (t), заданная на промежутке [t/,Z>], называется дифференцируемой в точке /о е [а,/?], если существует предел

lim

Этот предел называется производной вектор-функции г = г (!) в точке и обозначается г'(^о) • Итак,

r'(/₀) = lim

t-tо

Производная от вектор-функции в точке представляет собой вектор. Если же точку не фиксировать, то производной от век­тор-функции является также вектор-функция. Производная обо-

clr

значается г (!) или —.

dt

Теорема 5.1. Для того, чтобы вектор-функция r(t) =

= х(1) / + y(t) j + z(t) к была дифференцируемой в точке t₀, не­обходимо и достаточно, чтобы в этой точке были дифференци­руемы ее координаты x(t), y(t), z(t). При этом

г '{t)= х' (!) I + у' (!) j + z' (t) к

R(t)

Не координатами будут функции

*(0-*('₀) у(О-уОо) z(t)-z(t₀)

t — t_Q t — t_Q t — /q

По теореме 1 функция Rft) будет иметь предел тогда и только тогда, когда будут иметь пределы эти три функции. А так как пределами указанных функций служат их производные х' (t), у' (I) , z'ft), то г (/) дифференцируема, причем,

г \t)= x'(t) I + у'(t)j + z'(tj к .

Tеорема доказана.

§6. Техника дифференцирования

Пусть а = a(t), b = b(t), с = c(t) - три вектор-функции, а Я = ?Л) скалярная функция того же аргумента на промежутке [а. р]. Если все они являются непрерывными и дифференцируе­мыми в точке е[а, Р], то:

(14. ) Сумма aft) + bft) является дифференцируемой функцией в точке tо , причем

{aft) + b(t)) ' = a'(t) + b'ft)

2. Произведение Ml)- aft) является дифференцируемым в точке /о,причем

(Л/t)- aft))' = Я'(I) • aft) + Aft)- a'ft)

2. Скалярное произведение aft)- bft) является дифференцируе­мой функцией в точке I о и

(ia(t) b(t))' = a' ft)- bft) + aft)- b' ft)

2. Векторное произведение [a(t) ■ b(t)] является дифференцируе­мой функцией в точке /о и

[a(t)-bft)Y = [a'(t)-bft)] + [a(t)-b'ft)]

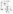
(u(t) ■ bit)- c(t))' = a'(t)- b(t)- c(t) + a(t) ■ b' (O' ^c(0 ⁺ a(t) ■ b(t) ■ c' (t).

Докажем, например, свойство 3. Пусть a(t) = х\ (t) 1 + Vi (t) j + z\ (t) к ; b(t) = x₂ (t) I + y₂ (t) j + z₂ (t) k.

Тогда a(t)‘ b(t) = X\ (t) x₂ (t) + y\ (t) y₂ (t) + z\ (t) z₂ (t). Продифференцируем, используя правила дифференцирования обычных функций:

(a(t)-b(t))' = x\'(t)x₂(t) +x\(t)x₂'(t) +y\'(t)y₂(t) +У\ (t)yi'(t) + f z,'(t) z₂(t) + z\(t)zi(t) = a'(t)- b(t) + a(t)-b'(t).

Аналогично доказываются остальные свойства.

§7. Производные высших порядков

Аналогично тому, как это делается в учебниках по мате­матическому анализу для функций одного аргумента, можно ввести понятие производных высших порядков для вектор- функций.

Производная г ’(t) от вектор-функции является также вектор-функцией, поэтому ее можно дифференцировать. Век­тор-функция г"{0 = (г ^f(tjy называегся второй производной от

d²r

вектор-функции г (t) и обозначается г" (t) или —— . Коорди-

dt

натами второй производной служат вторые производные от со­ответствующих координат исходной вектор-функции:

r"(t)=x"(t)I + y"(t)j + z"(t)k .

Дальнейшее дифференцирование приводит нас к треть­ей, четвертой, ..., /7-й производной. Используются обозначения

'"'"■IF "^m'lF

Будем говорить, что вектор-функция г = г (/), заданная на промежутке [a,b], принадлежит классу С^к , если она во всех точках промежутка имеет непрерывные производные до к-того

'

/*\ -¹- аА)- Ь' Ct\- c(t) + a(t) • b(t) • с' (t).

Ллииллшчио доказываются остл и : -s

-— - к

V

R

<Л

-

Vt

/» /У С

оражение определяет в npocipaifcr-

в е некоторый путь /. Вектор- функцию г = г (!) будем называть п араметрп чес к 11 м 11 ред ста в л ен и ем ну 1 и /.

Путь / называется регуляр­ным, если определяющая его век­тор-функция /*(/) е Су,, _/ч и всюду

на промежутке [а. b j г \t) *0.

Если к - 1, то путь называется гладким. Пусть путь / определяется вектор-функцией г = г (?), где t е \а, & ], а путь т вектор-функцией g = g(r), те [a, f3 ]

порядка включительно. Записывается: r(t)eC^_b]. Очевидно,

что вектор-функция г (t) принадлежит классу С тогда и толь­ко тогда, когда все ее координаты принадлежат классу С^к, то есть, имеют на промежутке [a,b] непрерывные производные до

A-того порядка.

Мы можем обычную скалярную функцию разложить в ряд Тейлора. Если мы это сделаем для каждой координаты век­тор-функции, то тем самым мы разложим вектор-функцию в ряд Тейлора:

r (0= x(t) i + у (I) j +z(t) к (1.1) 1

3 3 - з 2

lim a(t) = a₀ , lim b(t) = b₀ , lim A(/) = 17

lim (а(0 ± b(t)) = а₀ ± Ь₀ 17

lim X(t) a(t) = Я₀ -а₀ 17

lim a{t) • b(t) = а₀ ■ b_{) 17

t — t_Q t — t_Q t — /q 19

(Л/t)- aft))' = Я'(I) • aft) + Aft)- a'ft) 19

'"'"■IF "^m'lF 21

оражение определяет в npocipaifcr- 22

(12.1) 26