
- •Федеральное государственное образовательное бюджетное учреждение высшего профессионального образования
- •Предисловие
- •Методические рекомендации по ее изучению
- •Тема 1. Матрицы и определители
- •Тема 3. Векторные пространства
- •Тема 4. Линейные операторы
- •Тема 5. Квадратичные формы
- •§ 3.5], Или [3, § 3.8, 3.14], или [4, § 3.11, 3.13, 3.20]).
- •Тема 6. Элементы аналитической геометрии
- •Вопросы для самопроверки
- •Задачи для самоподготовки
- •Методические указания по выполнению контрольных работ
- •Варианты контрольных работ вариант 1
- •Контрольная работа № 1
- •Контрольная работа №2
- •Вариант 2 (для студентов, номера личных дел которых оканчиваются цифрой 2) Контрольная работа № 1
- •Контрольная работа №2
- •Вариант 3
- •Контрольная работа № 1
- •Контрольная работа №2
- •Вариант 4
- •Контрольная работа № 1
- •Контрольная работа №2
- •Вариант 5
- •Контрольная работа № 1
- •3. Определить, имеет ли однородная система
- •Контрольная работа №2
- •Вариант 6
- •Контрольная работа № 1
- •Контрольная работа №2
- •Вариант 7
- •Контрольная работа № 1
- •Контрольная работа №2
- •Вариант 8
- •Контрольная работа № 1
- •Контрольная работа №2
- •Вариант 9
- •Контрольная работа № 1
- •Контрольная работа №2
- •Вариант 10
- •Контрольная работа № 1
- •Контрольная работа №2
- •Примеры выполнения заданий контрольных работ
- •Литература Основная1
- •Дополнительная
- •Электронные ресурсы
- •Содержание
- •Линейная алгебра
Тема 4. Линейные операторы
Понятие линейного оператора. Образ и прообраз векторов. Матрица линейного оператора в заданном базисе. Ранг оператора. Операции над линейными операторами. Нулевой и тождественный операторы. Собственные векторы и собственные значения линейного оператора (матрицы). Характеристический многочлен матрицы. Диагональный вид матрицы линейного оператора в базисе, состоящем из его собственных векторов. ([1 или 5, § 3.6, 3.7]; [2 или 6, § 3.3, 3.4], или [3, § 3.6, 3.7, 3.12,3.13], или [4, § 3.8, 3.10, 3.18, 3.19]).
.
В этой теме рассматривается
одно из базовых понятий линейной алгебры
– понятие линейного оператора
(преобразования, отображения),
представляющего закон (правило), по
которому каждому вектору х
n-мерного
пространства
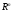 ставится в соответствие один векторy
m-мерного
пространства
ставится в соответствие один векторy
m-мерного
пространства
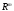 .
При
.
При оператор обращает
оператор обращает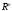 в себя.
в себя.
Линейность оператора
определяется выполнением свойств
аддитивности и однородности оператора
[1, или 5, или 3, § 3.6]. Нужно знать, что
каждому линейному оператору
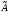 соответствует матрицаА
в некотором базисе
соответствует матрицаА
в некотором базисе
 .
Верно и обратное утверждение
.
Верно и обратное утверждение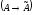 .
С помощью этой матрицы для любого векторах
можно найти его образ – вектор y.
.
С помощью этой матрицы для любого векторах
можно найти его образ – вектор y.
Особую роль в приложениях
линейной алгебры играют векторы, которые
под воздействием линейного оператора
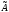 преобразуются в новые векторы, коллинеарные
исходным. Такие векторы получили название
собственных векторов оператора
преобразуются в новые векторы, коллинеарные
исходным. Такие векторы получили название
собственных векторов оператора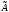 (матрицыА),
а соответствующие им числа – собственных
значений оператора
(матрицыА),
а соответствующие им числа – собственных
значений оператора
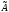 (матрицыА).
Точные определения и нахождение
собственных векторов и значений приведены
в [1, или 5, или 3, пример 3.7].
(матрицыА).
Точные определения и нахождение
собственных векторов и значений приведены
в [1, или 5, или 3, пример 3.7].
Если базис линейного оператора составить из собственных векторов, то матрица оператора имеет наиболее простой вид и представляет собой диагональную матрицу, а соответствующая операция называется приведением данной матрицы к диагональному виду ([1, или 5, или 3, пример 3.8]).
Тема 5. Квадратичные формы
Квадратичная форма (определение). Матрица квадратичной формы. Матричная форма записи квадратичной формы.. Канонический вид и ранг квадратичной формы. Закон инерции квадратичных форм. Положительно и отрицательно определенная, знакоопределенная квадратичные формы. Критерий определенности квадратичной формы через собственные значения ее матрицы. Критерий Сильвестра. ([1 или 5, § 3.8]; [2 или 6,
§ 3.5], Или [3, § 3.8, 3.14], или [4, § 3.11, 3.13, 3.20]).
Квадратичные формы достаточно
часто возникают при решении прикладных
задач. Если в n-мерном
линейном пространстве выбрать некоторый
базис, то квадратичную форму
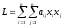 можно рассматривать как некоторую
функцию векторного аргумента
можно рассматривать как некоторую
функцию векторного аргумента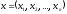 .
.
Необходимо знать определение и матричную запись квадратичной формы, ее канонический вид. Уметь приводить в простых случаях квадратичную форму к каноническому виду, имея в виду, что это возможно сделать многими способами, но ранг квадратичной формы при этом не меняется.
Студент должен владеть
двумя способами исследования на
знакоопределенность квадратичной формы
(с помощью собственных значений ее
матрицы и критерия Сильвестра). Например,
очевидно, что квадратичная форма
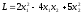 (т.е.
(т.е.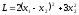 )
является знакоположительной. В этом
можно убедиться с помощью отмеченных
критериев, ибо матрица квадратичной
формы
)
является знакоположительной. В этом
можно убедиться с помощью отмеченных
критериев, ибо матрица квадратичной
формы ,
как нетрудно показать, имеет положительные
собственные значения
,
как нетрудно показать, имеет положительные
собственные значения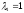 ,
,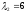 ,
а угловые (главные) миноры
,
а угловые (главные) миноры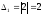 ,
,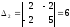 также положительные. А квадратичная
форма
также положительные. А квадратичная
форма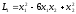 не является знакоопределенной, так как
ее матрица
не является знакоопределенной, так как
ее матрица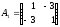 имеет разные по знаку собственные
значения
имеет разные по знаку собственные
значения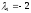 и
и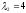 ,
а угловые миноры
,
а угловые миноры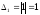 ,
,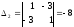 чередуются по знаку, начиная с
положительного значения (при
чередуются по знаку, начиная с
положительного значения (при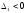 ,
,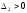 квадратичная форма была бы знакоотрицательной)
– (см. [1 или 5, примеры 3.11, 3.12], или [3,
примеры 3.11, 3.12, 3.109, 3.110]).
квадратичная форма была бы знакоотрицательной)
– (см. [1 или 5, примеры 3.11, 3.12], или [3,
примеры 3.11, 3.12, 3.109, 3.110]).
