Обратные функции.

Пусть - биекция (т.е. каждый элемент из множестваявля­ется образом единственного элемента из множества).

Определим функцию . Другими словами, если функцияэлементпереводит в, тоэлементпереводит в

- биекция;называется обратной функцией к.

Для любой биекции выполняются свойства:

1. , Где- единичная функция на.

Для доказательства свойства проверим два усло­вия определения равенства функций.

а) ,

б) . Вычислим

Из а) и б) следует .

2. ,где- единичная функция на.

Для доказательства свойства проверим два усло­вия определения равенства функций.

а) ,

б) . Вычислим.

Из а) и б) следует .

Теорема. Функцияимеет обратную тогда и только тогда, когда- биекция.

Доказательство следует из определения.

Следствие. Любая строго монотонная функция имеет обратную функцию. При этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).

Замечание. График обратной функции симметричен графику данной функции относительно биссектрисы 1 и 3 координатных углов.

Элементарные функции.

Основными элементарными функцияминазываются следующие функции: показательная функция, степенная функция, логарифмическая функция, тригонометрические функции, обратные тригонометрические функции.

Дома– построить графики этих функций и определить их вид.

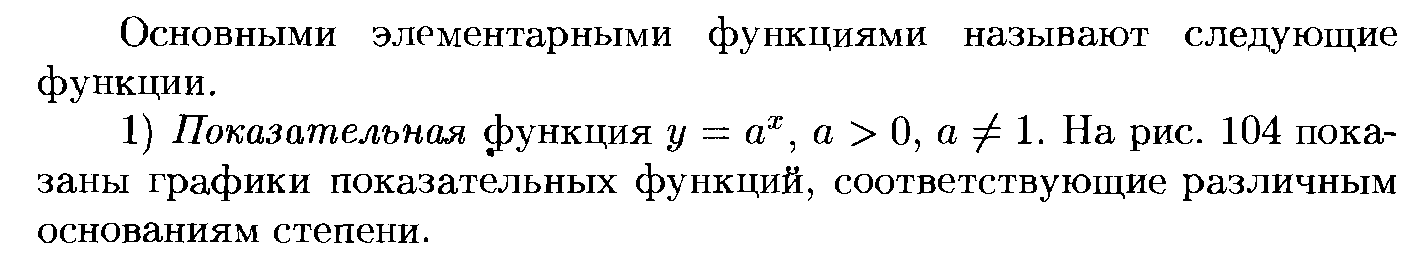
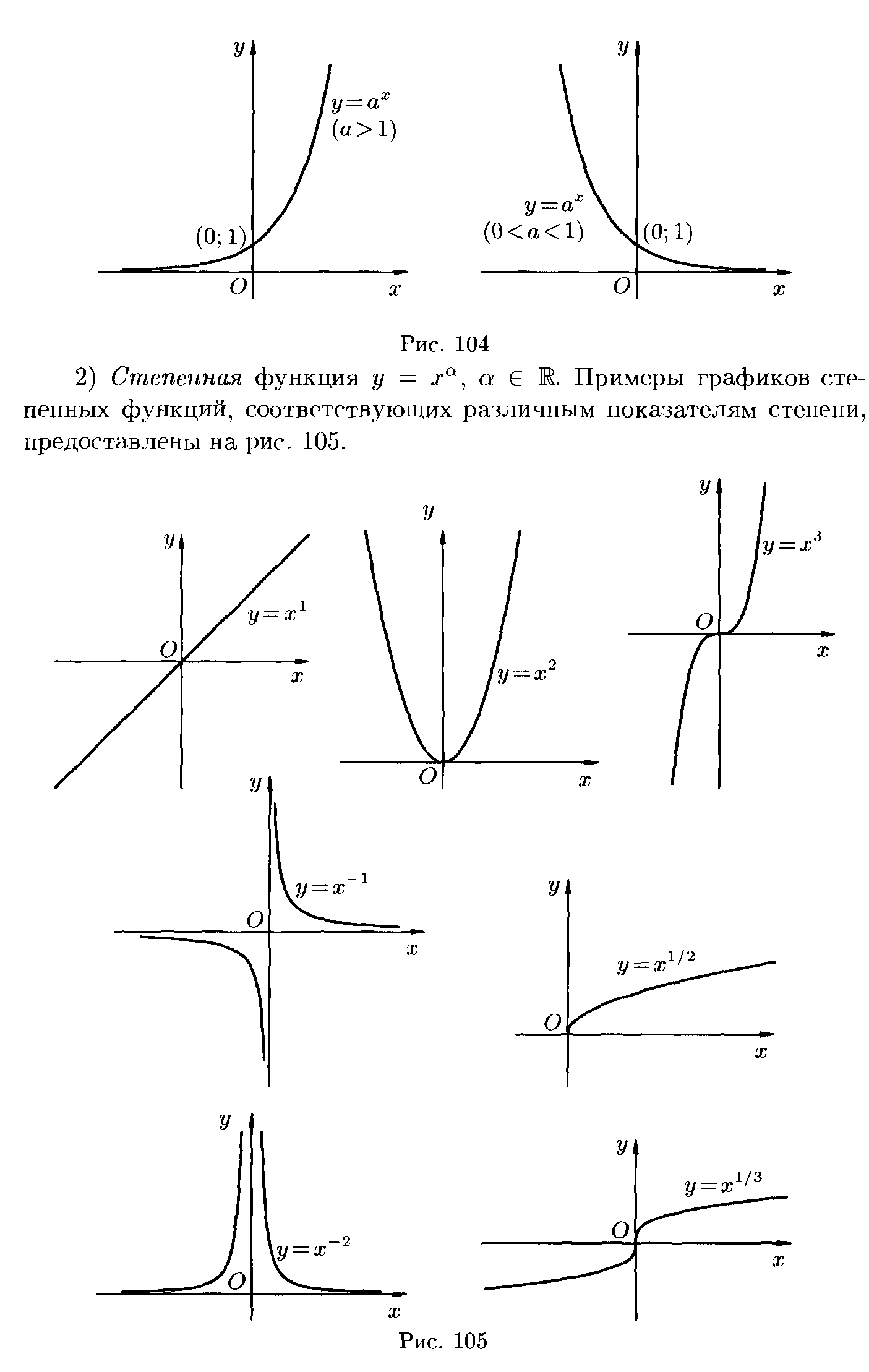
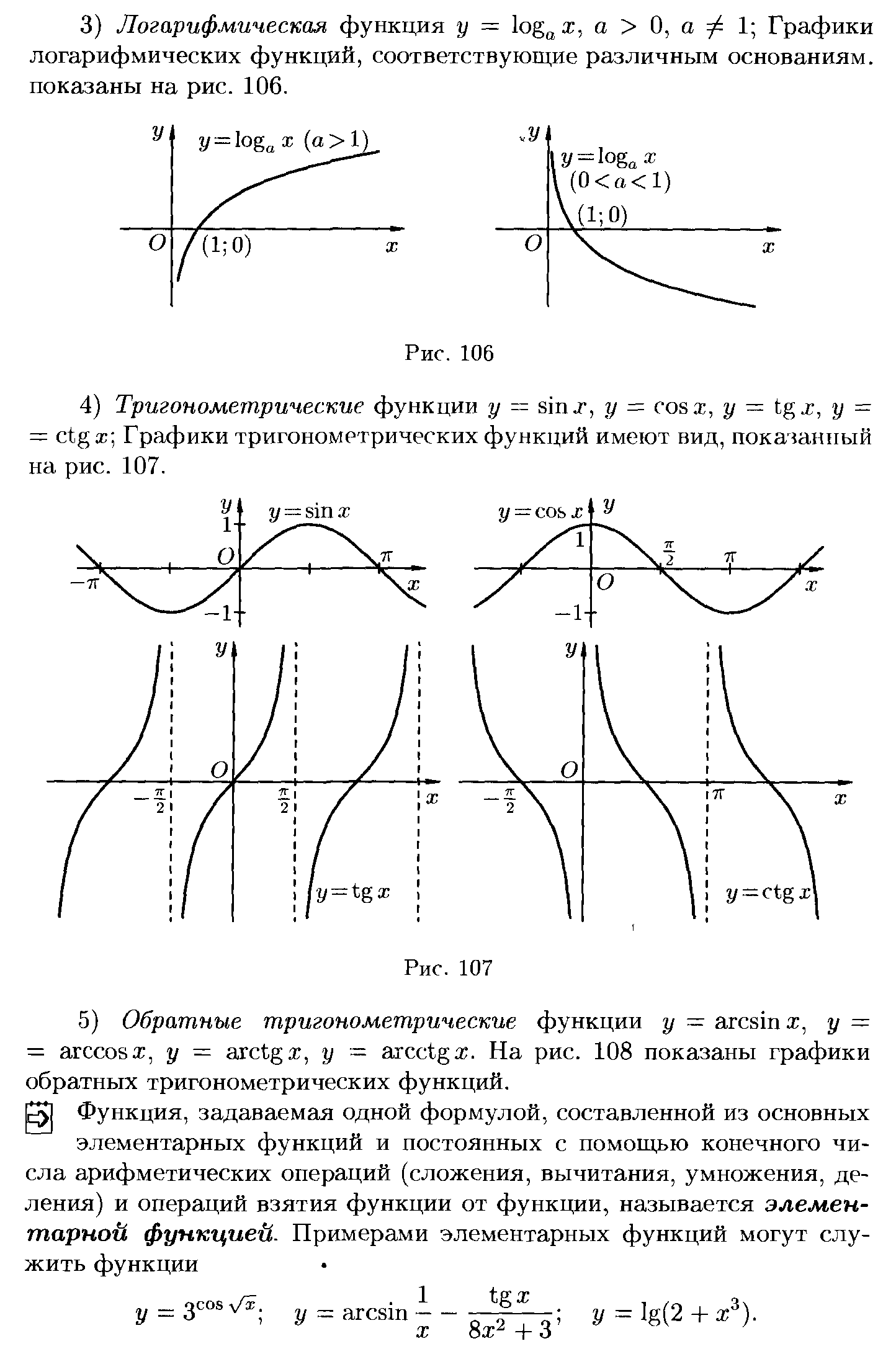
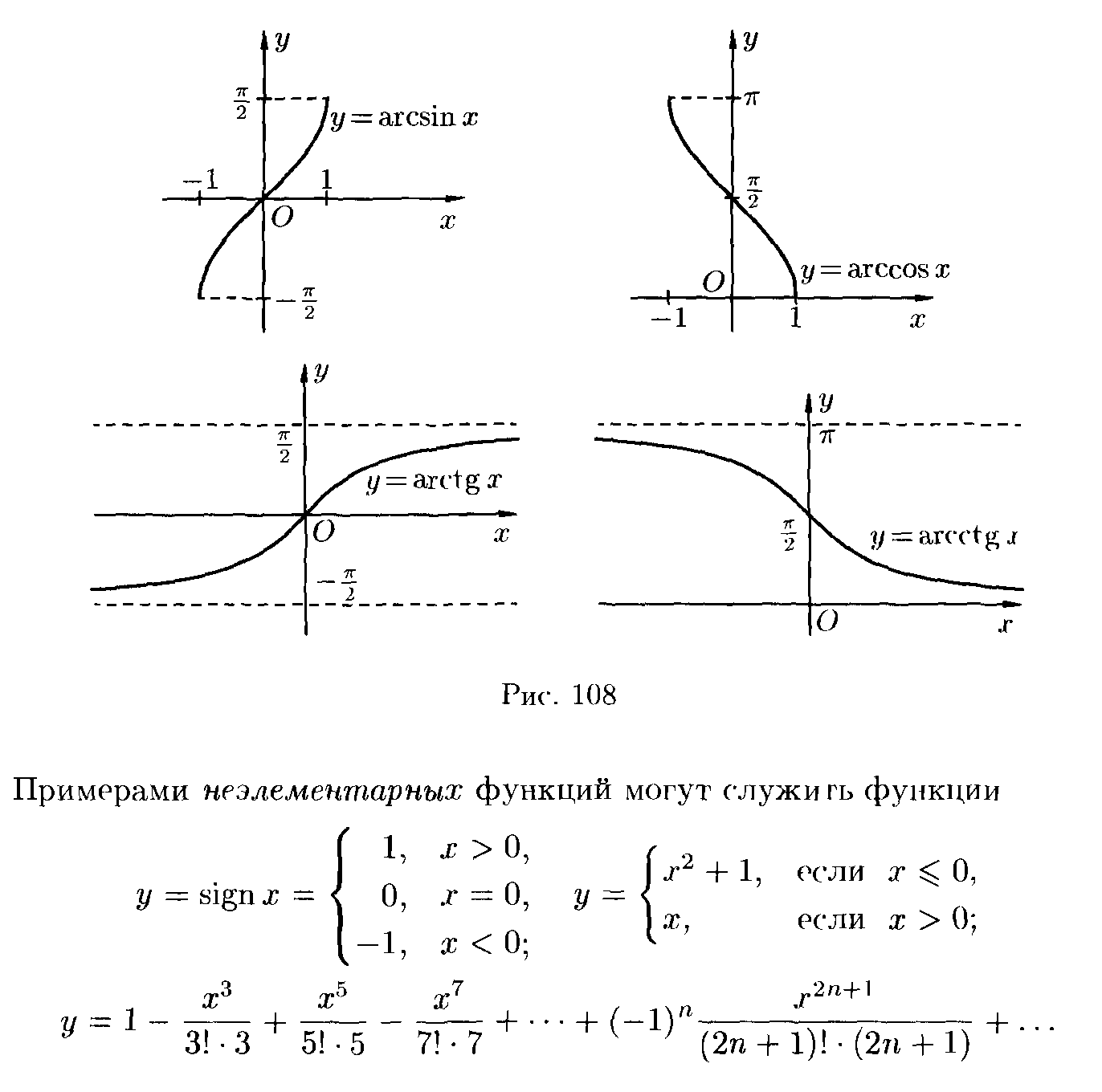
Э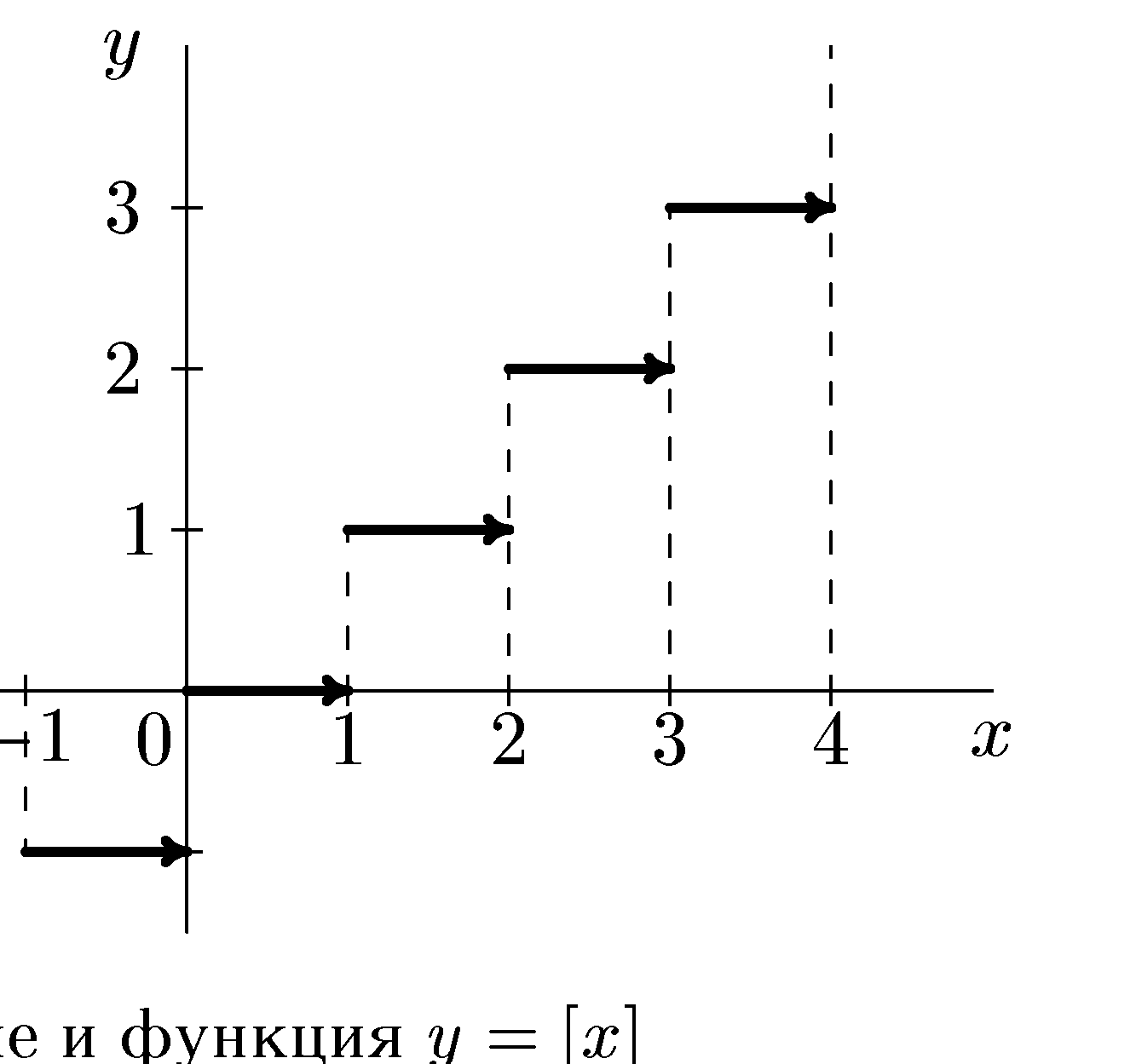лементарной функциейназывается функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных с помощью допустимых действий (т.е. конечного числа арифметических операций: сложения, вычитания, умножения, деления и операции композиции).

Примером неэлементарной функции является

функция целая часть числа:

Целая часть числа равна наибольшему целому числу,не превосходящемуНапример,

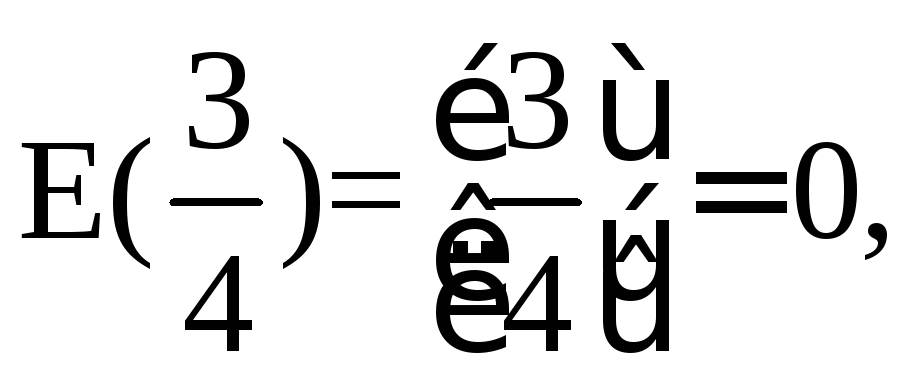
Примером неэлементарной функции является также функция дробная часть числа. Это функциязначение которой вычисляется по формуле:Например,;;;

Обратные тригонометрические функции.

1. Функция .

Рассмотрим функцию ;

Эта функция не является инъекцией, является сюръекцией, не является биекцией. Следовательно, не имеет обратной функции.

Рассмотрим сужение sin:;

Это сужение является инъекцией, сюръекцией, биекцией.

Следовательно имеет обратную функцию.

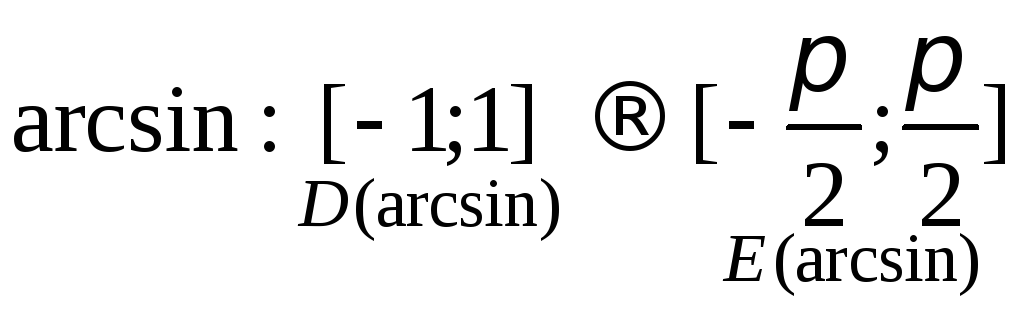
График функцииarcsinсимметричен графику функции сужения функцииsinнаотносительно биссектрисы 1 и 3 координатных углов.

у =arcsinх

Свойства.

,,

,,

.

2. Функция .

Рассмотрим функцию ;:

Эта функция не является инъекцией, является сюръекцией, не является биекцией. Следовательно, не имеет обратной функции.

Рассмотрим сужение cos:

;

Это сужение является инъекцией, сюръекцией, биекцией. Следовательно имеет обратную функцию:

График функции arccosсимметричен графику функции сужения функцииcosнаотносительно биссектрисы 1 и 3 координатных углов.

.

у = х

Свойства х.

,,

,,

.

Самостоятельно построить графики остальных обратных тригонометрических функций.