
- •Математический анализ. Часть 1.
- •Раздел 1. Введение в анализ: множества, функции.
- •Операции над высказываниями.
- •Предикаты. Кванторы общности и существования. Определение предиката.
- •Квантор общности.
- •Квантор существования.
- •П.2. Элементы теорий множеств (интуитивная теория множеств). Числовые множества. Множество действительных чисел.
- •Подмножества.
- •Операции над множествами.
- •Свойства операций над множествами.
- •1. Законы коммутативности.
- •2. Законы ассоциативности.
- •Универсальные множества. Дополнение и его свойства.
- •Бинарные отношения.
- •Запишем это бинарное отношение как множество пар:
- •Сужение функции.
- •Виды функций.
- •Композиция функций (сложная функция, суперпозиция функций.
- •Тождественная (единичная) функция.
- •Обратные функции.
- •1. , Где- единичная функция на.
- •Обратные тригонометрические функции.
- •2. Функция .
- •3. Функция arctg.
Подмножества.
Определение. Множество![]() называется подмножеством
называется подмножеством![]() ,
если каждый элемент из множества
,
если каждый элемент из множества![]() лежит во множестве
лежит во множестве![]() ,
пишут:
,
пишут:![]() .
Другими словами:
.
Другими словами:
(![]() )
)![]() - истина.
- истина.
Для любых множеств
![]() ,
,![]() ,
,![]() выполняются свойства:
выполняются свойства:
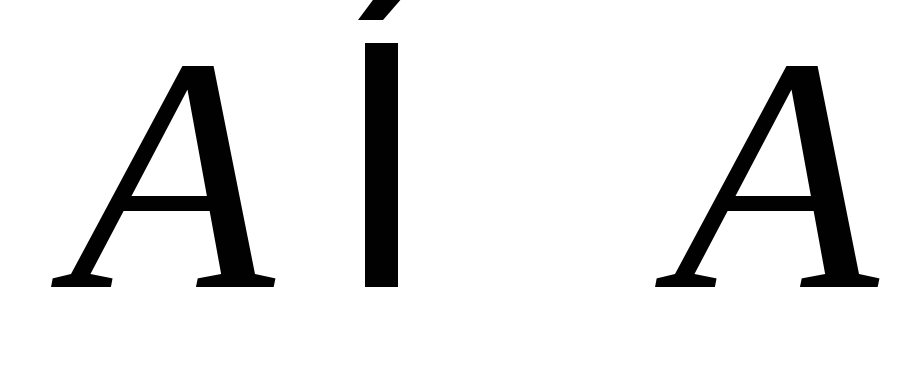 ,
это свойство рефлективности.
,
это свойство рефлективности.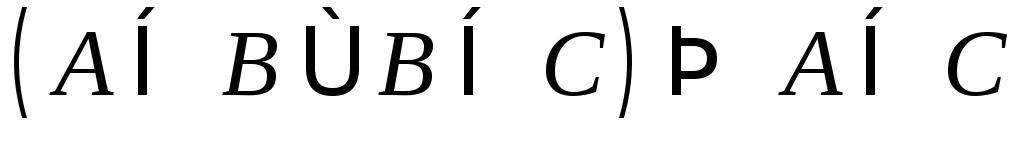 .
Это свойство транзитивности.
.
Это свойство транзитивности.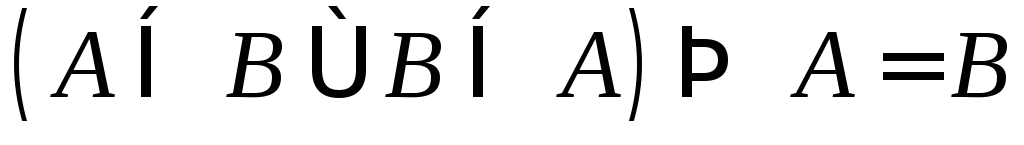 .
Это свойство антисимметричности.
.
Это свойство антисимметричности.
Определение.Множества, элементами которых являются числа, называются числовыми. Примерами числовых множеств являются
![]() -
множество натуральных чисел:
-
множество натуральных чисел:![]()
![]() -
множество натуральных чисел и нуль:
-
множество натуральных чисел и нуль:![]()
![]() -
множество целых чисел:
-
множество целых чисел:![]()
![]() -
множество действительных чисел.
-
множество действительных чисел.
![]() -
множество положительных действительных
чисел:
-
множество положительных действительных
чисел:![]() ,
,
![]() -
множество отрицательных действительных
чисел:
-
множество отрицательных действительных
чисел:![]() ,
,
![]() -
множество положительных действительных
чисел и нуль:
-
множество положительных действительных
чисел и нуль:![]() ,
,
Между этими множествами существует соотношение:
![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() .
.
Множество действительных чисел обладает следующими свойствами.
1) Оно упорядоченное: для любых двух
различных чисел
![]() и
и![]() имеет место одно из двух соотношений
имеет место одно из двух соотношений![]() либо
либо![]() .
.
2) Множество
![]() плотное: между любыми двумя различными
числами
плотное: между любыми двумя различными
числами![]() и
и![]() содержится бесконечное множество
действительных чисел
содержится бесконечное множество
действительных чисел![]() ,
то есть чисел, удовлетворяющих неравенству
,
то есть чисел, удовлетворяющих неравенству![]() .
.
3) Множество
![]() непрерывное.
непрерывное.
Свойство непрерывности позволяет установить взаимно-однозначное соответствие между множеством всех действительных чисел и множеством всех точек прямой. Это означает, что каждому действительному числу соответствует определённая (единственная) точка числовой оси и, наоборот, каждой точке оси соответствует определённое (единственное) действительное число. Поэтому вместо слова «число» часто говорят «точка».
Пусть
![]() и
и![]() – действительные числа, причем
– действительные числа, причем![]() .
.
Числовыми промежутками (интервалами) называют подмножества действительных чисел, имеющих следующий вид:
![]() – отрезок (сегмент, замкнутый промежуток);
– отрезок (сегмент, замкнутый промежуток);
![]() – интервал (открытый промежуток);
– интервал (открытый промежуток);
![]() ;
;![]() – полуоткрытые интервалы (или
полуоткрытые промежутки);
– полуоткрытые интервалы (или
полуоткрытые промежутки);
![]() ;
;![]() ;
;
![]() ;
;![]() ;
;
![]()
– бесконечные интервалы (промежутки).
Числа
![]() и
и![]() называют соответственнолевымиправым концамиэтих промежутков.
Символы
называют соответственнолевымиправым концамиэтих промежутков.
Символы![]() и
и![]() не числа, это символическое обозначение
процесса неограниченного удаления
точек числовой оси от начала 0 влево и
вправо.
не числа, это символическое обозначение
процесса неограниченного удаления
точек числовой оси от начала 0 влево и
вправо.
Обозначение. Если![]()
![]() ,
то их сумму можно записать в виде:
,
то их сумму можно записать в виде:
![]() ;
;
их произведение – в виде:
![]() .
.
Определение.Окрестностью точки![]() называется любой интервал
называется любой интервал![]() ,
содержащий точку
,
содержащий точку![]() .
В частности, интервал
.
В частности, интервал![]() ,
где
,
где![]() ,
называется
,
называется![]() -
окрестностью точки
-
окрестностью точки![]() ;
число
;
число![]() называется центром, а число
называется центром, а число![]() радиусом.
радиусом.
![]() -
аналитическая запись окрестности
конечной точки.
-
аналитическая запись окрестности
конечной точки.
Окрестностью точки
![]() называется
внешняя часть любого промежутка, т.е.
называется
внешняя часть любого промежутка, т.е.![]() .
.
Определение. Множество![]()
![]() называется ограниченным, если оно
целиком содержится в некотором интервале.
называется ограниченным, если оно
целиком содержится в некотором интервале.
Замечание. Ограниченность множества![]() означает,
что существует такое число
означает,
что существует такое число![]() ,
что координаты любой точки из
,
что координаты любой точки из![]() по
модулю не превосходят
по
модулю не превосходят![]() .
(
.
(![]() ).
).
Пустое множество.
Определение. Множество, не содержащее
ни одного элемента, называется пустым
множеством. Обозначается:![]() .
.
![]() .
.
Свойства пустых множеств.
Пустое множество единственно.
Доказательство:
![]() ,
,![]() - пустые множества.
- пустые множества.![]() .
.
Пустое множество является подмножеством любого множества.
Мощность множества. Счётные и несчётные множества.
Множества бывают конечные и бесконечные.
Определение. Мощностью конечного
множества называется число элементов
этого множества. Обозначается![]() -
мощность конечного множества
-
мощность конечного множества![]() .
.
Пусть
![]() Множества
Множества![]() и
и![]() - равномощные множества. (Они не равны,
они равномощны).
- равномощные множества. (Они не равны,
они равномощны).
Первым вопросом, возникшим в применении
к бесконечным множествам был вопрос о
возможности их количественного сравнения
между собой. Ответ на этот и близкие
вопросы был дан Г. Кантором в конце 70-х
годов 19 века. Эта теория опирается на
взаимно однозначное соответствие между
двумя множествами. Рассмотрим множество
натуральных чисел
![]()
![]() =
=![]() .
Если можно установить взаимно однозначное
соответствие, то говорят, что множество
.
Если можно установить взаимно однозначное
соответствие, то говорят, что множество![]() -
счётное множество. Если нельзя установить
взаимно однозначное соответствие между
бесконечным множеством
-
счётное множество. Если нельзя установить
взаимно однозначное соответствие между
бесконечным множеством![]() и
множеством натуральных чисел
и
множеством натуральных чисел![]() ,
то говорят, что множество
,
то говорят, что множество![]() -
несчётное множество. Мощность счётных
множеств – есть наименьшая мощность,
которую может иметь бесконечное
множество. Кантор доказал, что множество
всех рациональных чисел счётно, а
множество всех действительных чисел
несчётно.
-
несчётное множество. Мощность счётных
множеств – есть наименьшая мощность,
которую может иметь бесконечное
множество. Кантор доказал, что множество
всех рациональных чисел счётно, а
множество всех действительных чисел
несчётно.
Определение. Мощность множества
действительных чисел называется
мощностью континуума или мощностью![]() .
.
Множеству всех действительных чисел равномощны:
1) множество всех точек плоскости, 2) множество всех подмножеств счётного множества, 3) множество всех комплексных чисел, …
Гипотеза Кантора. Всякое множество, состоящее из действительных чисел, либо конечно, либо счётно, либо равномощно множеству всех действительных чисел.
