4.3. Матрицы билинейной формы

Выберем в n-мерном пространстве какой-либо базиси выразим билинейную форму через коэффициенты ивекторов и в этом базисе. Имеем:

В силу свойств а) и б) пункта билинейной формы, имеем:

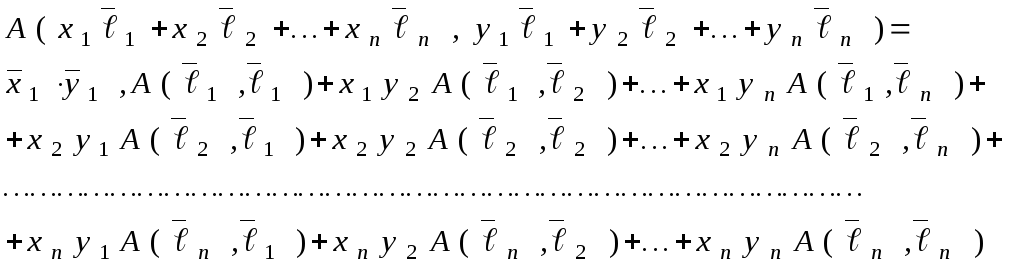
Или, короче:

.

Обозначим постоянные через. Тогда в заданном базисевсякая билинейная форма вn-мерном пространстве может быть записана в виде:

. (5)

ОПРЕДЕЛЕНИЕ 4. Матрицу , составленную из коэффициентовмногочлена (5), называютматрицей билинейной формы в базисе

Таким образом, в каждом базисе пространства билинейная форма определяется своей матрицей:

.

4.4. Преобразование матрицы билинейной формы при изменении базиса

Пусть даны в n-мерном линейном пространстве два базиса:и. Причем, векторы второго базисавыражаются через векторы базисаформулами:

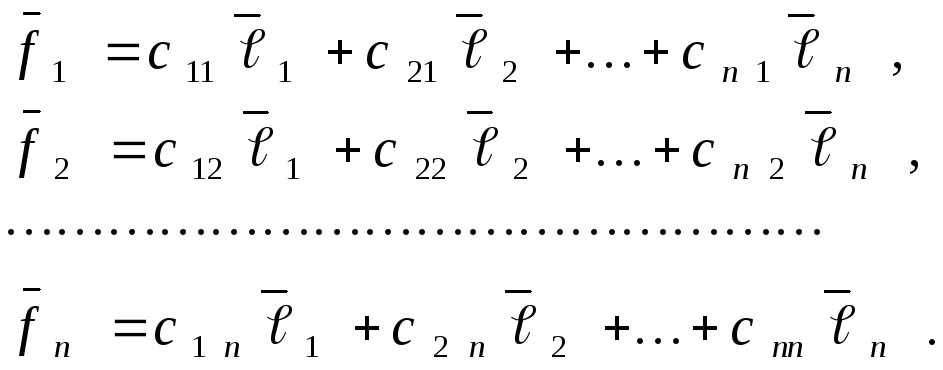
Матрицу

назовем матрицей перехода от базиса к базису.

Пусть есть матрица билинейной формы в базисе , аматрица той же билинейной формы в базисе. Наша задача состоит в том, чтобы по матриценайти матрицу.

По определению , то есть- значение билинейной формы при .

Для того, чтобы найти это значение, то есть , воспользуемся формулой (5), подставив в нее вместоикоординаты векторовив базисе, то есть числаи. Получим:

. (6)

Это и есть искомая формула.

Запишем ее в матричной форме. Для этого положим . Таким образом,является элементами матрицы, транспонированной к матрицеС. С учетом этого выражение (6) можно записать так:

или

.

Итак, если А и В суть матрицы билинейной формы соответственно в базисах и., то преобразование матрицы билинейной формы при переходе от одного базиса к другому будет иметь вид:

где С- матрица перехода от базисак базису., а- транспонированная матрица.

4.5. Квадратичные формы

Пусть -симметричная билинейная форма.

ОПРЕДЕЛЕНИЕ 1. Функция , которая получается из билинейной формы , если положить в ней =, называется квадратичной формой.

Всякая квадратичная форма , в базисе евклидового пространстваЕ_n выражается следующей формулой:

, (7)

где симметричная матрицаквадратичной формы и.

В некотором базисе выражение (7) квадратичной формы может не содержать произведений , то есть

, (8)

Выражение (8) называется каноническим видом квадратичной формы. В частности, если , то получаемнормальный вид квадратичной формы .

Для всякой квадратичной формы существует такой базис, в котором она имеет канонический вид.

4.6. Методы приведения квадратичной формы к каноническому виду

а) Метод Лагранжа выделения полных квадратов.

Пусть квадратичная форма имеет в базисе вид (7). Для приведения формы к сумме квадратов методом Лагранжа рассмотрим случай квадратичной формы, у которой все коэффициенты (при квадратах ), равны нулю и в то же время эта квадратичная форма не равна тождественно нулю, то есть в ней есть отличное от нуля хотя бы одной произведение, например, .

Выполним преобразование базиса, при котором коэффициенты векторов в старом и новом базисах связаны формулами:

.

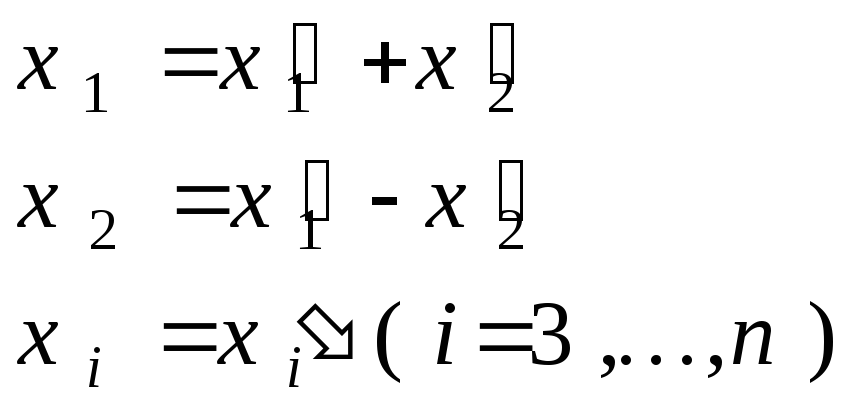Тогда:

.

Таким образом, всегда найдется такой базис, в котором в записи (7) хотя бы один коэффициент при квадрате .отличен от нуля.

В дальнейшем будем считать, что . (Если, то отличен от нуля коэффициент при квадрате какой-нибудь другой координаты и к рассматриваемому случаю можно прийти, иначе, занумеровав векторы, что также является некоторым преобразованием базиса).

Рассмотрим часть квадратичной формы, содержащей , то есть

.

Дополним эту сумму до полного квадрата:

,

где есть алгебраическая сумма членов, не зависящих от. Если теперь сделать замену

то квадратичная форма в новом базисе примет вид

.

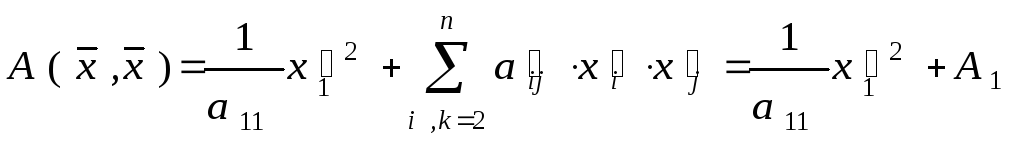В полученной форме выделено слагаемое , а оставшаяся частьА, является квадратичной формой в .

Далее эти рассуждения повторяются для исходной квадратичной формы и т.д. Конечным результатом является то, что она приводится к нормальной форме.

ПРИМЕР 1. Методом Лагранжа привести к каноническому виду квадратичную форму

.

Первое преобразование:

.

Тогда получим:

.

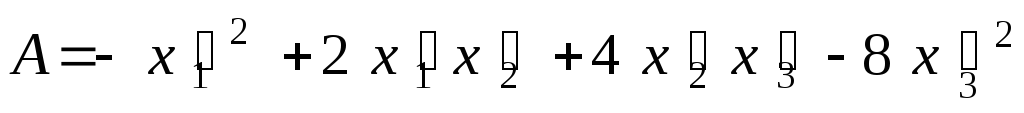Второе преобразование:

.

Получим новое выражение для квадратичной формы:

.

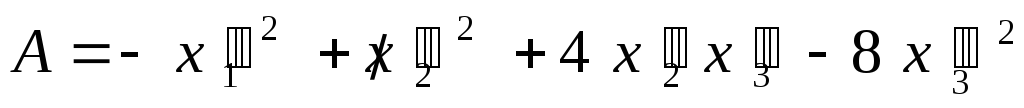Третье преобразование:

.

форма примет канонический вид:

.

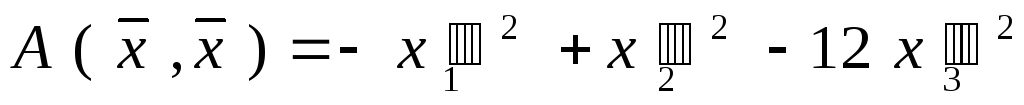При этом

.

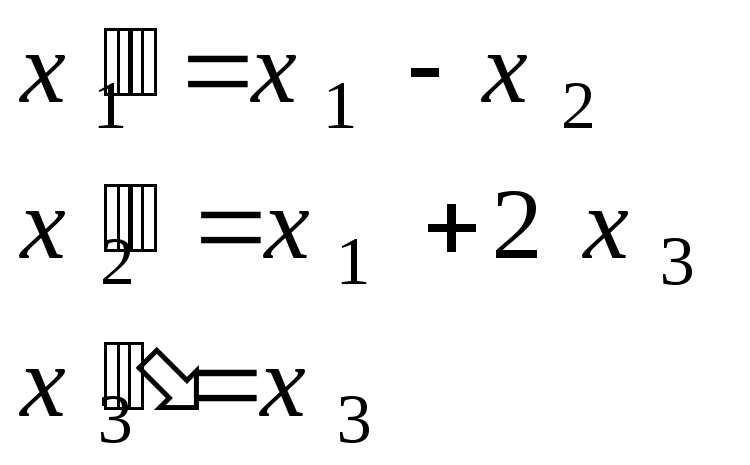б) Метод собственных векторов.