Глава V. Нелинейное программирование
Методы нелинейного
программирования – это численные методы
отыскания минимума (максимума) функций
многих переменных при наличии ограничений
типа равенств и неравенств, имеющих
нелинейный вид, т.е. требуется найти
такой вектор
,
при котором функция
(5.1)
достигает минимума, при выполнении ограничений
,
,
; (5.2)
,
. (5.3)
Метод линеаризации.
Суть метода линеаризации заключается
в следующем. Выполняется линеаризация
всех соотношений (5.1) – (5.3). Для этого
применяется разложение в ряд Тейлора
с удержанием только линейных составляющих.
Разложение выполняется в окрестности
точки
,
которой следует задаться. Итак, вместо
(5.1) – (5.3) имеем для k-той
итерации:
;
,
;
,
, (5.4)
где векторы
,
,
.
Соотношения (5.4) позволяют решать задачу линейного программирования.
Таким образом,
может быть построена последовательность
точек
,
которая, вообще говоря, может привести
к точке
,
являющийся решением задачи (5.1) – (5.3).
Пример. Минимизировать
(5.5)
при ограничениях
;
;
(5.6)
Пусть
.
Линеаризованные соотношения
; (5.7)
; (5.8)
.
и соотношения
(5.9)
определяют задачу
линейного программирования. Решив эту
задачу, найдем точку первого приближения
,
затем находится точка
и т.д.
Рассмотрим геометрическую интерпретацию задачи этого примера. На рис. 5.1 приведены графики, соответствующие ограничениям (5.6) и (5.8), (5.9).
З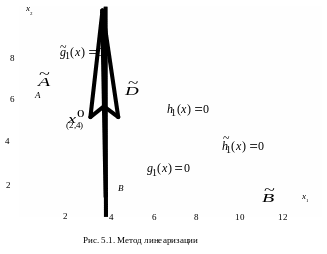
адача
(5.5), (5.6) предполагает нахождение на дуге
АВ
такой точки, в которой целевая функция
(5.5) достигает минимума. Решение этой
задачи известно, это точка A.
В результате
линеаризации геометрическая интерпретация
задачи изменилась. Теперь среди точек
прямой
требуется найти такую точку, в которой
функция (5.7) достигает минимума. Как было
сказано выше, это задача определяется
соотношениями (5.7) – (5.9). Оправдано,
однако, добавление к этим соотношениям
дополнительных неравенств, которые бы
ограничивали область поиска решения.
Эти дополнительные ограничения вводятся
из следующих соображений. Ошибка
линеаризации по мере удаления от точки
все больше и больше возрастает, см.,
например, зависимости
и
.
В таких условиях вполне оправдано
введение ограничений
;
,
г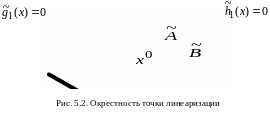
де
и
некоторые положительные числа. Полученная
при этом новая допустимая область
показана на рис. 5.1 и 5.2.
Таким образом, уже
среди точек отрезка
должна быть найдена точка, в которой
целевая функция (5.7) достигает минимума.
Совершенно аналогично следует поступать при любой итерации, причем, числа и от итерации к итерации следует постепенно уменьшать.
Алгоритм нелинейного программирования
Излагаемый ниже алгоритм позволяет решать задачу нелинейного программирования в постановке (5.1) – (5.3).
В качестве начальной
точки
может быть выбрана любая точка, т.е. как
точка, принадлежащая допустимой области
D
(определяется ограничениями (5.2), (5.3)),
так и точки, не принадлежащие ей. Если
,
то в первую очередь организуется
наискорейший спуск «почти в область
D»,
а затем включается в работу метод
линеаризации. Если
,
то сразу применяется метод линеаризации.
Рассмотрим, что входит в понятие «почти в область D» и как организуется наискорейший спуск в эту область. «Почти областью D» называется вся совокупность точек x, для которых имеют место ограничения
,
; (5.10)
,
, (5.11)
где
,
– некоторые малые положительные числа.
Эти числа должны быть такими, что
выполнение условий (5.10) может расцениваться
как практически удовлетворительное
выполнение равенств
, ,
(строго говоря, точного выполнения этих равенств практически добиться не возможно вообще). Таким образом, «почти область D» определяется ограничениями (5.10), (5.11).
Наискорейший спуск почти в область D осуществляется в результате минимизации функции
, (5.12)
где
,
– весовые константы,
Как только
обратится в ноль, решается задача
линейного программирования, затем вновь
проверяются все ограничения и т.д. Задача
(5.5), (5.6) по этому методу решается примерно
так, как это показано на рис. 5.3.
Н
а
этом рисунке
,
;
,
– траектории спуска «почти в область
D»,
,
;
,
– траектории, соответствующие методу
линеаризации.