
Метод допустимых направлений
Этот метод предназначен для отыскания минимума функции при наличии ограничений только в виде неравенств, т.е.
; (5.12)
![]()
![]() ,
,
![]() , (5.13)
, (5.13)
где
![]() .
Поиск точки минимума должен всегда
начинаться из точки
.
Поиск точки минимума должен всегда
начинаться из точки
![]() ,
(в области Dg
выполнены
все ограничения (5.13)), т.е. из допустимой
точки.
,
(в области Dg
выполнены
все ограничения (5.13)), т.е. из допустимой
точки.
Суть метода заключается в следующем.
Вначале линеаризуются соотношения (5.12), (5.13):
![]() ; (5.14)
; (5.14)
![]() ,
, (5.15)
,
, (5.15)
где
![]() – номер итерации,
– номер итерации,
![]() .
Наиболее благоприятное направление
перехода (точка
.
Наиболее благоприятное направление
перехода (точка
![]() )
определяется в результате решения
вспомогательной задачи:
)
определяется в результате решения
вспомогательной задачи:
![]() , (5.16)
, (5.16)
где скаляр
![]() и вектор
и вектор
![]() подлежат определению. С этой целью,
подставив (5.16) в (5.14), (5.15), потребуем,
чтобы имел место
подлежат определению. С этой целью,
подставив (5.16) в (5.14), (5.15), потребуем,
чтобы имел место

при условии
![]() ,
.
,
.
Поскольку
![]() и
и
![]() ,
то точка
определяется из условия, что функция
,
то точка
определяется из условия, что функция
![]() (5.17)
(5.17)
достигает минимума при условии
![]() ,
. (5.18)
,
. (5.18)
Любой вектор
![]() ,
удовлетворяющий неравенствам (5.18),
является допустимым вектором. Они
определяют допустимые направления.
Среди всех допустимых направлений
выделим такое, которое обеспечивает
наибольшую минимизирующую поправку к
значению функции
,
удовлетворяющий неравенствам (5.18),
является допустимым вектором. Они
определяют допустимые направления.
Среди всех допустимых направлений
выделим такое, которое обеспечивает
наибольшую минимизирующую поправку к
значению функции
![]() на шаге от точки
на шаге от точки
![]() к точке
к точке
![]() путем решения следующей задачи линейного
программирования – минимизировать
функцию
путем решения следующей задачи линейного
программирования – минимизировать
функцию
(5.19)
при ограничениях
![]() ,
. (5.20)
,
. (5.20)
Допустим, что имеет место такое решение, что,
![]() ,
,
тогда определяется
максимальная длина шага
![]() ,
осуществляемого в направлении
без выхода за пределы допустимой области,
которая определяется ограничениями
рис. 5.4
,
осуществляемого в направлении
без выхода за пределы допустимой области,
которая определяется ограничениями
рис. 5.4
 ,
, (5.21)
,
, (5.21)
Другими словами,
![]() .
.
и проверкой
выполнения ограничений (5.21). Затем
определяется такое значение
![]() ,
которое удовлетворяет условию
,
которое удовлетворяет условию
![]()
и для которого
![]() достигает минимума. Поиск такого значения
параметра
осуществляется любым однопараметрическим
методом поиска (методом дихотомии,
золотого сечения и т.п.). В итоге
определяется точка
достигает минимума. Поиск такого значения
параметра
осуществляется любым однопараметрическим
методом поиска (методом дихотомии,
золотого сечения и т.п.). В итоге
определяется точка
.
Далее осуществляется
переход к
![]() -й
итерации.
-й
итерации.
Метод отсекающих плоскостей (Алгоритм Келли)
Найти такие значения
![]() ,
,
![]() ,
которых целевая функция
,
которых целевая функция
![]() (5.22)
(5.22)
достигает минимума при выполнении ограничений
![]() (5.23)
(5.23)
Последняя группа
неравенств может отсутствовать. В
эквивалентной постановке требуется
найти такую точку
![]() в области D,
чтобы у
достигала минимума. Заметим:
в области D,
чтобы у
достигала минимума. Заметим:
а) если некоторая конкретная задача содержит еще и ограничения типа равенств
![]() ,
,
![]() ,
, (5.24)
,
, (5.24)
то они обращаются в неравенства
![]() ,
,
![]() , (5.26)
, (5.26)
где
![]() – некоторые положительные числа, такие,
что выполнение неравенств (5.25) может
быть принято как выполнение ограничения
(5.24);
– некоторые положительные числа, такие,
что выполнение неравенств (5.25) может
быть принято как выполнение ограничения
(5.24);
б) если целевая функция имеет вид
![]() ,
,
то такая задача сводится к исходной: найти min функции
![]()
при условии, что
![]() (5.27)
(5.27)
![]() ,
,
,
,
г де
де
![]() – новая переменная.
– новая переменная.
Каким бы ни было
значение
,
должно быть меньше
(согласно
![]() ).
Вместе с тем min
y
достигается при
).
Вместе с тем min
y
достигается при
![]() ,
т.о. эта задача эквивалентна исходной.
,
т.о. эта задача эквивалентна исходной.
Последовательность операций.
1. Вместо области
D
задаем область
![]() в виде n-мерного
куба, включающего D,
т.е.
в виде n-мерного
куба, включающего D,
т.е.
![]() .
.
Например, при
![]() область
может быть назначена так, как это показано
на рис. 5.5.
область
может быть назначена так, как это показано
на рис. 5.5.
2. Решается задача отыскания минимума функции
(5.28)
при условии выполнения ограничений
![]() ,
. (5.29)
,
. (5.29)
Ограничения (5.29) включают в себя и ограничения исходные.
Это задача линейного
программирования. Решив ее, найдем точку
![]() .
Возможны следующие случаи:
.
Возможны следующие случаи:
а)
![]() ,
тогда задача решена;
,
тогда задача решена;
б)
![]() ,
т.е. имеются
,
т.е. имеются
![]() .
Тогда переходим к п.3.
.
Тогда переходим к п.3.
3. От области отрезается некоторая область, содержащая точку . Для этого среди не выполнившихся ограничений выбирается одно, которое наиболее сильно нарушено (допустим, это ограничение под номером k0), оно линеаризуется в точке :
![]() ,
,
где
![]() – градиент функции
– градиент функции
![]() ,
записанный для точки
,
записанный для точки
![]() .
.
Накладываем требование, чтобы
![]() . (5.30)
. (5.30)
Заметим, что это
требование отсекает часть области
,
куда входит
.
Действительно, условию (5.30) никогда не
может удовлетворить точка
,
т.к. при подстановке в него
получим
![]() ,
что противоречит условию
,
что противоречит условию
![]() .
.
Уравнение
![]()
есть уравнение плоскости. Решается задача
– min;
![]() ,
,
,
,
![]() ;
;
![]() .
.
Это задача линейного
программирования. Получаем точку
![]() ,
и т.д.
,
и т.д.
Процесс вычислений заканчивается при выполнении исхода а) п.2.
Пример. Задача:
![]() – min;
– min;
![]() ;
;
![]() .
.
Геометрическая интерпретация рассмотрена на рис. 5.6
П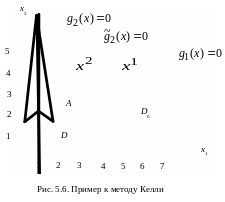 роследим
ход решения по методу Келли.
роследим
ход решения по методу Келли.
Область определим неравенствами:
![]() ,
,
![]() .
.
Задача линейного программирования
– min;
;
дает точку
![]() .
В этой точке
.
В этой точке
![]() ;
;
![]() .
.
Линеаризуем
![]() в точке
:
в точке
:
![]() ,
,
![]() .
.
Заметим, что
![]() не удовлетворяет этому ограничению:
не удовлетворяет этому ограничению:
![]() .
.
Решается задача:
– min;
;
;
![]() .
.
Решив задачу линейного программирования, получаем точку , и т.д.
Вычисления прекращаются тогда, когда для всех задействованных ограничений получим, что
![]() ,
,
,
,
где
![]() – некоторые положительные числа,
задаваемые из соображений необходимой
точности решения задачи.
– некоторые положительные числа,
задаваемые из соображений необходимой
точности решения задачи.
