
- •ЛинейнОе пространство
- •Определения. Базис и размерность. Разложение вектора по базису пространства
- •Определение базиса и размерность пространства l
- •Если обладает базисом, то говорят, что линейное пространствоLимеет рангQ (ranq q).
- •Изоморфизм n-мерных линейных пространств
- •Формулы преобразования координат при изменении базиса
- •Произведением. Евклидово пространство
- •2.1. Определение евклидова пространства. Длина вектора. Неравенство Коши-Буняковского
- •2.2. Ортогональный и орто-нормированный базисы в пространстве е
- •2.3. Ортогонализация базиса в пространстве
- •2.4. Скалярное произведение векторов в евклидовом пространстве
- •Изоморфизм евклидовых пространств
- •§ 3. Билинейные квадратичные формы
- •4.1. Линейная функция
- •4.2. Билинейные формы
- •4.3. Матрицы билинейной формы
- •4.4. Преобразование матрицы билинейной формы при изменении базиса
- •4.5. Квадратичные формы
- •4.6. Методы приведения квадратичной формы к каноническому виду
- •Будем рассматривать квадратичную форму (7) в евклидовом пространстве
2.2. Ортогональный и орто-нормированный базисы в пространстве е
В линейном пространстве у нас нет оснований предпочесть одни базисы другим. Там все базисы равноправны. В евклидовом пространстве существуют наиболее удобные базисы, а именно, ортогональные базисы. Они играют здесь ту же роль, что и прямоугольные системы координат в аналитической геометрии.
ОПРЕДЕЛЕНИЕ
5. Будем говорить, что n
векторов
![]() ни один из которых не равен нулю, образуютортогональный
базис в
n-мерном евклидовом
пространстве
ни один из которых не равен нулю, образуютортогональный
базис в
n-мерном евклидовом
пространстве
![]() ,
если они попарно ортогональны, то есть:
,
если они попарно ортогональны, то есть:
![]() при
при
![]() .
.
ОПРЕДЕЛЕНИЕ
6. Векторы
![]() ни один из которых не равен нулю, образуютортогональный
нормированный базис,
если они попарно ортогональны и имеют
каждый длину равную единице, то есть,
если выполняется равенство:
ни один из которых не равен нулю, образуютортогональный
нормированный базис,
если они попарно ортогональны и имеют
каждый длину равную единице, то есть,
если выполняется равенство:
![]() (9)
(9)
Для того, чтобы
данное нами определение ортогонального
и ортонормированных базисов было
корректным, необходимо доказать, что
входящие в определение векторы
![]() действительно образуют базис, то есть
являются линейно независимыми.
действительно образуют базис, то есть
являются линейно независимыми.
Докажем, что равенство
![]() (10)
(10)
возможно лишь,
если
![]() ,
то есть является тривиальным. Умножим
обе части равенства (10) скалярно на
,
то есть является тривиальным. Умножим
обе части равенства (10) скалярно на![]() .
Получим:
.
Получим:
![]() .
.
Но по определению ортогонального базиса
![]() при
при
![]() .
.
Следовательно,
![]() Аналогично,
умножая (10) на
Аналогично,
умножая (10) на
![]() ,
получим2=0
и т. д. Таким образом, соотношение (10)
выполнено, если
,
получим2=0
и т. д. Таким образом, соотношение (10)
выполнено, если
![]() ,
то есть векторы
,
то есть векторы![]() являются независимы, что и доказывает
корректность утверждения.
являются независимы, что и доказывает
корректность утверждения.
Чтобы доказать
существование ортогональных базисов
в евклидовом пространстве
![]() ,
воспользуемся, так называемым, процессом
ортогонализации.
,
воспользуемся, так называемым, процессом
ортогонализации.
2.3. Ортогонализация базиса в пространстве
Процесс ортогонализации
состоит в том, что из не ортогональных,
но линейно независимых векторов
![]() ,
можно построить систему попарно
ортогональных векторов
,
можно построить систему попарно
ортогональных векторов![]() .
Опишем процесс их построения. Пусть
даныn
линейно независимых векторов
.
Опишем процесс их построения. Пусть
даныn
линейно независимых векторов
![]() .
По этим векторам построимn
попарно ортогональных векторов
.
По этим векторам построимn
попарно ортогональных векторов
![]() .
Сначала положим
.
Сначала положим![]() .
Вектор
.
Вектор![]() будем искать в виде:
будем искать в виде:![]() ,
где число1
подберем таким образом, чтобы выполнялось
условие
,
где число1
подберем таким образом, чтобы выполнялось
условие
![]() .
.
Имеем:
![]() (11)
(11)
Предположим, что
построена система попарно ортогональных
и отличных от нуля векторов
![]() .
Далее вектор
.
Далее вектор![]() будем определять так:
будем определять так:
![]()
![]() ,
(12)
,
(12)
то есть вектор
![]() мы получаем из вектора
мы получаем из вектора![]() путем "исправления" его с помощью
линейной комбинации уже построенных
векторов
путем "исправления" его с помощью
линейной комбинации уже построенных
векторов![]() .
.
Коэффициенты
![]() находим из условия ортогональности
вектора
находим из условия ортогональности
вектора![]()
![]() к
векторам
к
векторам![]() .
Последовательно умножим соотношение
(12) на
.
Последовательно умножим соотношение
(12) на![]() ,
затем на
,
затем на![]() и т.д. Имеем
и т.д. Имеем
![]()
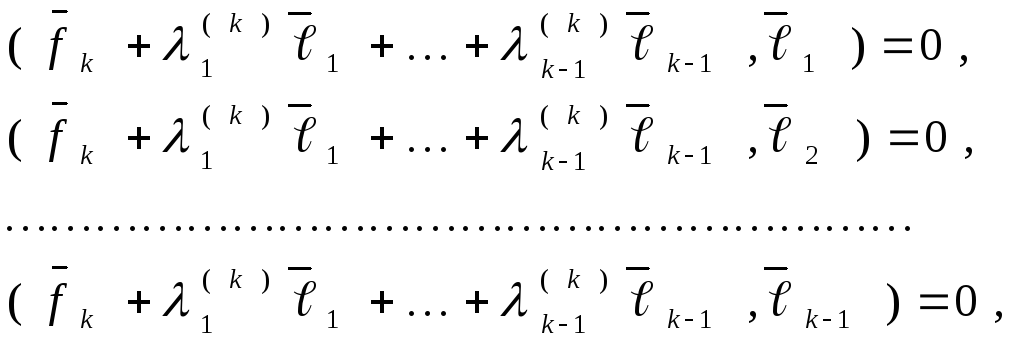 ( 13)
( 13)
Так как векторы
![]() попарно ортогональны, то равенства (13)
запишутся так:
попарно ортогональны, то равенства (13)
запишутся так:
![]()
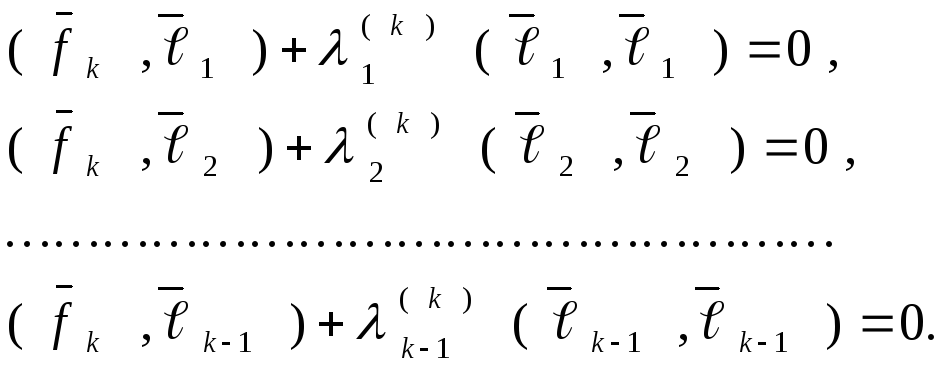
Отсюда находим:
![]() (14)
(14)
До сих пор не было
использовано то, что векторы
![]() линейно независимы. Это будем использовать
при доказательстве того, что построенный
вектор
линейно независимы. Это будем использовать
при доказательстве того, что построенный
вектор![]() отличен от нуля. Заметим предварительно,
что вектор
отличен от нуля. Заметим предварительно,
что вектор![]() есть линейная комбинация векторов
есть линейная комбинация векторов![]() .
Но, с другой стороны, вектор
.
Но, с другой стороны, вектор![]() можно заменить линейной комбинацией
можно заменить линейной комбинацией ![]() и векторов
и векторов
![]() .
В итоге, вектор
.
В итоге, вектор![]() записывается в виде:
записывается в виде:
![]()
![]() .
(15)
.
(15)
Теперь ясно, что
![]() .Так
как, в противном случае, правая часть
равенства (15) была бы нулем, что противоречит
линейной независимости векторов
.Так
как, в противном случае, правая часть
равенства (15) была бы нулем, что противоречит
линейной независимости векторов![]() .
.
Итак, доказано,
что
![]() .
.
Мы построили по
векторам
![]() и
и![]() вектор
вектор![]() .
Таким же образом по
.
Таким же образом по![]() и
и![]() мы построим
мы построим ![]() и т.д.
и т.д.
Продолжая этот
процесс до тех пор, пока не будут исчерпаны
заданные векторы
![]() .
Получаемn
отличных от нуля и попарно ортогональных
векторов
.
Получаемn
отличных от нуля и попарно ортогональных
векторов
![]() ,
которые образуют ортогональный базис
в исходном евклидовом пространстве
,
которые образуют ортогональный базис
в исходном евклидовом пространстве![]() .
.
Т е о р е м а 4. Во
всяком n-мерном
евклидовом пространстве
![]() существует ортогональный базис.
существует ортогональный базис.
Д о к а з а т е л ь
с т в о. По определению n-мерного
пространства
![]() в нем существует базис линейно независимых
векторов
в нем существует базис линейно независимых
векторов![]() .
С помощью процесса ортогонализации из
векторов
.
С помощью процесса ортогонализации из
векторов![]() можно построить ортогональный базис
можно построить ортогональный базис![]() ,
что и доказывает теорему.
,
что и доказывает теорему.
