3. Изоморфизм n-мерных линейных пространств

ОПРЕДЕЛЕНИЕ 6. Два линейных пространства и называются изоморфными, если между векторами иможно установить взаимно однозначное соответствиетак, что если векторусоответствует вектор, а векторусоответствует вектори выполнены условия:

Вектору соответствует. (11)

Вектору соответствует. (12)

Из определения изоморфизма следует, что если из . а векторы - из , то

в соответствии с равенствами (11) - (12) получаем, что линейно независимым векторам из соответствуют линейно независимые векторы из и обратно.

Заметим, что два линейных пространства различной размерности не изоморфны друг другу.

3. Формулы преобразования координат при изменении базиса

Пусть идва различных базиса в. Каждый из векторов базисаразложим по базисуследующим образом:

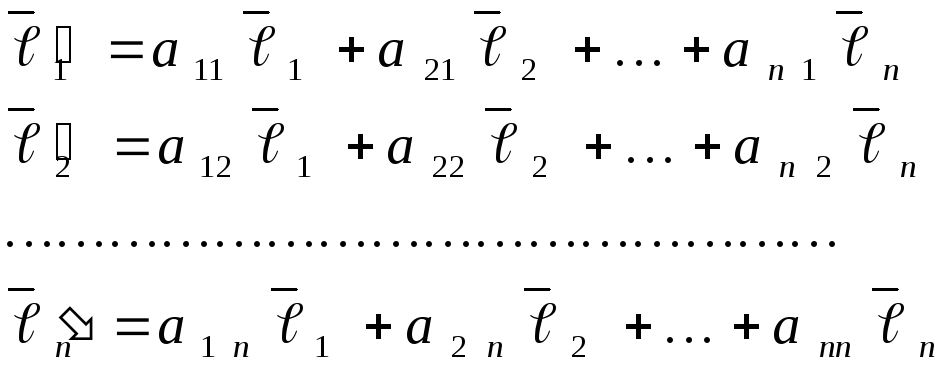. (13)

ОПРЕДЕЛЕНИЕ 7. Матрицей перехода от базисак базису называется матрица вида:

,

в которой i-й столбец есть коэффициенты i-го уравнения системы (13).

Далее обозначим через коэффициенты векторав первом базисе , а черезего координаты во втором базисе . Пусть требуется найти связь координатчерез.

Имеем:

или

. (14)

Подставим в правую часть выражения (14) вместо их выражения (13). Получим:

(15)

или

Так как, система векторов линейно независима, то координаты при них в правой и левой частях равенства должны быть равны.

Имеем

,

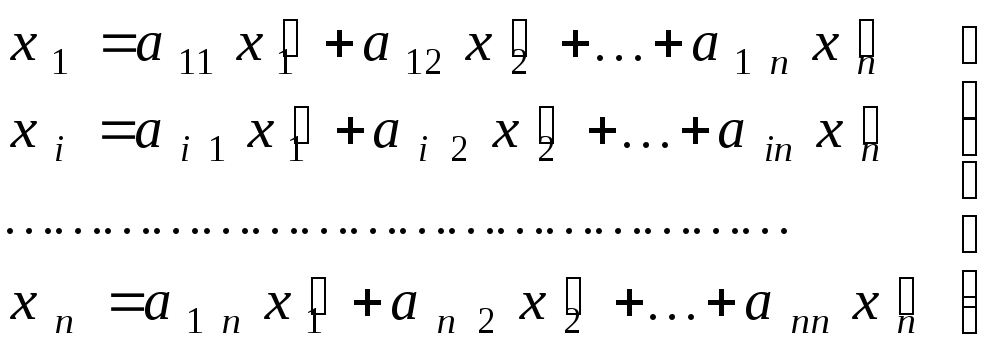или

(16)

где

.

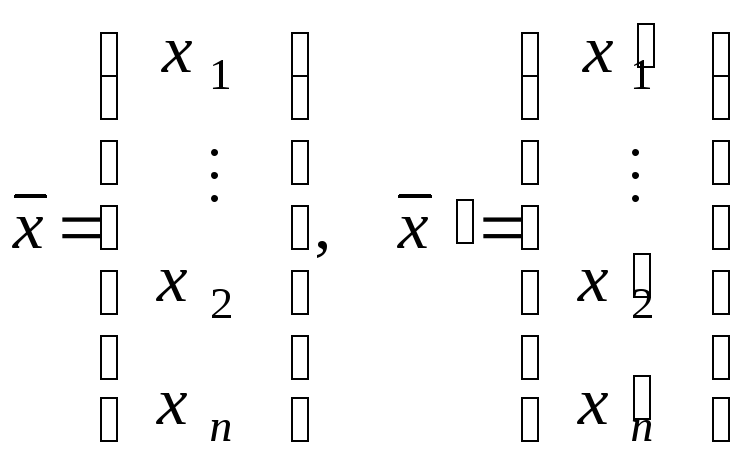Таким образом, координаты вектора в базисе выражаются через координаты того же вектора во втором базисе с помощью матрицы , то есть матрицы, транспонированной к .

Поскольку матрица является невырожденной, то из формулы (16) можно получить:

(17)

где координаты вектораво втором базисе выражаются через координатыв первом базисе с помощью матрицы , являющейся обратной к .

ПРИМЕР. Найти координаты вектора в базисе , состоящем из векторов .

Решение. В соответствие с формулой (13) имеем:

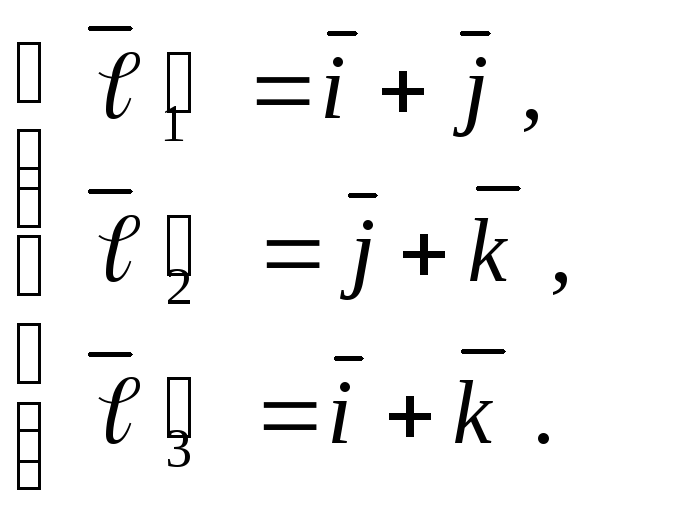
Запишем матрицы перехода и .

.

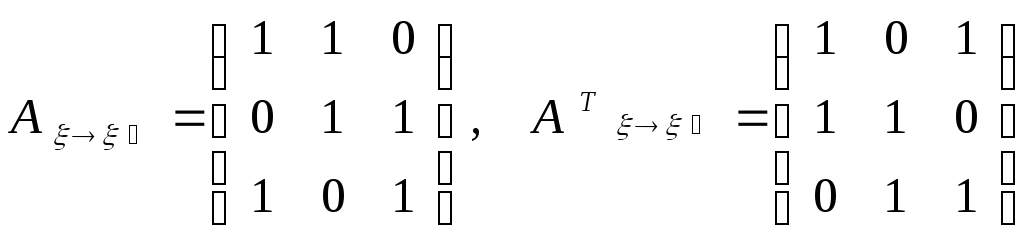Обращая матрицу . и используя формулу (17), находим

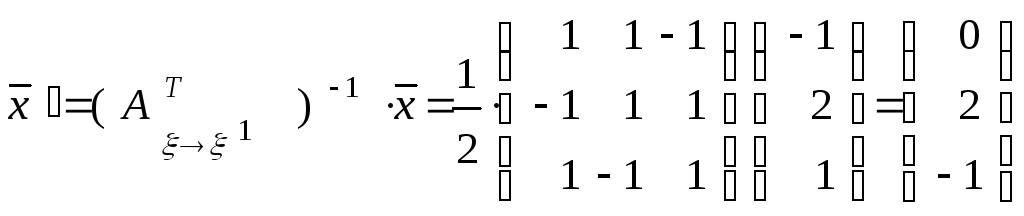
То есть

.

Откуда координаты вектора в базисепринимают значения

.

2. ЛИНЕЙНОЕ Пространство со скалярным

Произведением. Евклидово пространство

ОПРЕДЕЛЕНИЕ 1. Действительное линейное пространство L называется евклидовым, пространством Е, если каждой паре векторов поставлено в соответствие действительное число, обозначаемое символомилии называется скалярным произведением векторовии определенное с помощью соотношения:

, (1)

где длины векторови, есть угол между этими векторами.

Для скалярного произведения векторов должны выполняться следующие условия:

1º. ,

2º. ,

3º. ,

4º. (причем).

2.1. Определение евклидова пространства. Длина вектора. Неравенство Коши-Буняковского

ОПРЕДЕЛЕНИЕ 2. Длиной вектора в евклидовом пространстве называется число равное:

(2)

ОПРЕДЕЛЕНИЕ 3. Углом между векторами и мы назовем число, определенное выражением:

, (3)

или

. (4)

ОПРЕДЕЛЕНИЕ 4. Векторы иназываются ортогональными, если угол между ними равен .

В этом случае из формулы (1) следует:

(,)=0. (5)

Н е р а в е н с т в о К о ш и- Б у н я к о в с к о г о. Так как косинус угла между двумя векторами определяется выражением (4)

, (6)

то

.

Откуда

.

или

. (7)

Неравенство (7) называется неравенством Коши-Буняковского.

Если скалярное произведение задается формулой

причем

,

то неравенство (7) примет вид

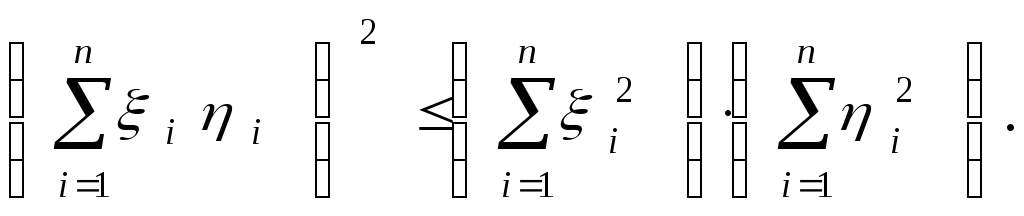
Т е о р е м а. 3. Для любых векторов ив евклидовом пространстве Е имеет место неравенство:

. (8)

Д о к а з а т е л ь с т в о.

.

Так как , то

то есть

,

что и требовалось доказать.