2.4. Скалярное произведение векторов в евклидовом пространстве

Пусть - ортогональный базис евклидова пространстваЕ. Найдем, как выражается скалярное произведение двух векторов через их координаты в этом базисе.

Пусть - координаты вектора, а- координаты векторав этом базисе, то есть:

Тогда:

(16)

Если базис является ортонормированным, то есть

, (17)

то выражение (16) в таком базисе примет вид

). (18)

Таким образом, в нормированном ортогональном базисе скалярное произведение двух векторов равно сумме произведений их соответствующих координат.

5. Изоморфизм евклидовых пространств

Если рассмотреть ряд n-мерных евклидовых пространств, то эти пространства могут отличаться одно от другого во всяком случае способом задания векторов базиса. Возникает вопрос: какие из этих пространств действительно различны и какие различия являются лишь чисто внешними?

Для того, чтобы вопрос был точно поставлен, нужно определить, какие два

евклидова пространства будем считать несущественно различающимися (изоморфными).

ОПРЕДЕЛЕНИЕ 7. Два евклидовых пространства и называются изоморфными, если между их элементами можно установить взаимно однозначное соответствие так, что:

1. Еслии, то.

2. Если, то.

3. Еслии, то.

Таким образом, два евклидовых пространства и изоморфны, если они изоморфны как линейные пространства. И этот изоморфизм таков, что он сохраняет скалярное произведение соответствующих векторов.

§ 3. Билинейные квадратичные формы

4.1. Линейная функция

Рассмотрим простейшие числовые функции, аргументами которых являются вектора. Простейшей числовой функцией в пространстве L является линейная функция.

ОПРЕДЕЛЕНИЕ 1. Функция называетсялинейной, если ставит в соответствие число и при этом выполнены условия:

.

.

Выберем в n-мерном линейном пространстве базис. Так как каждый векторможно представить в виде:

,

то в силу свойства линейной функции имеем:

.

Итак, в линейном n-мерном пространстве с заданным базисом линейная функция может быть представлена в виде

, (1)

где постоянные, зависящие лишь от выбора базиса, а- координаты векторав этом базисе.

Выясним, как меняются коэффициенты линейной функции при замене одного базиса другим.

Пусть и- два базиса в. Предположим, что векторывыражаются через векторы базисаследующим образом:

,

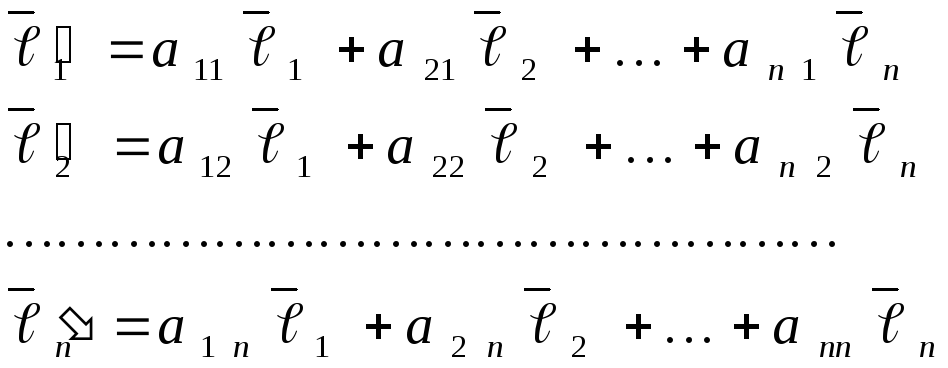В базисе линейная функцияопределяется выражением

, (2)

а в базисе - выражением

. (3)

Так как

то

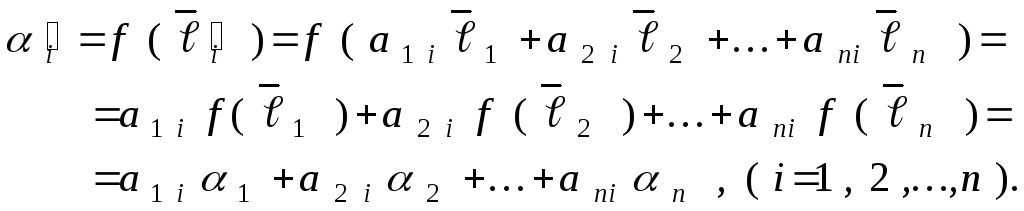
Следовательно, коэффициенты линейной формы преобразуются при переходе к другому базису так же, как векторы базиса этого пространства.

4.2. Билинейные формы

ОПРЕДЕЛЕНИЕ 2. Выражение называется билинейной функцией (билинейной формой) от векторов и ,если:

. При фиксированном есть линейная функция от , то есть:

а) ,

б) .

. При фиксированном есть линейная функция от , то есть:

а) ,

б) .

ОПРЕДЕЛЕНИЕ 3. Билинейная функция (форма) называется симметричной, если для всех векторов и имеет место равенство:

(4)

В частности, из определения скалярного произведения в евклидовом пространстве Е следует, что это произведение является симметричной билинейной формой.