zaicevVM_2

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1) (1 – ex)yy′= ex;

8.2. Решить задачу Коши:

, y(1) = 2.

.pdf

Скачиваний:

Добавлен:

14.02.2015

Размер:

1.33 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 169 10 11 12 13 14 15 16 > Следующая >>>

3. xy′– y = x / arctg xy , y(1) = 0.

5. 2(y′+ y) = xy2 , y(1) = 2.

7. xy′= 2 x2 + y2 + y, y(1) = 2.

xy′cos

= ycos

– x,

y(1) = 0.

11. 3y′+2xy = 2 xy−2 e−2 x2 ,

y(0)= 1.

13. xy′sin

+ x = y sin

y(1) = 0.

15.

x2y′– 4x2 – xy = 0,

y(1) = 0.

17.

yy′= 3y – 2x,

y(1) = 1.

19.

y′+

x + 1

ex , y(1) = e.

21.

y′+ xy =(1+x)e–xy2,

y(0)= 1.

23.

2(y′+ xy) = (x – 1)exy2,

y(0) = 2.

25.

(x– y)dx+ (x + y)dy = 0 , y(2) = 1.

27.

y′– 4xy = – 4x3 , y(0) = – 0,5.

29.

xdy – ydx = x e

dx , y(1) = 0.

2) xdy – ydx = x2 + y2 dx.

2. y′– x2+y1 = ex (x + 1)2, y(0) = 1.

4.y′+ 2xy = e−x2 s in x , y(0) = 1.

6.xy′= 2 (y – xy ), y(1) = 4.

xy′+ 6y =

2 y

y(1) = 4.

10. xy + y2 =(2x – y)xy′,

y(1) = 1.

12. (xex +

)dx –

dy = 0, y(1) =5.

y′–

= 1.

14.

= x sin x , y

16. 2xy′+ 3y = x ,	y(4) = 2.
18. xy′+ y = xy2ln x,	y(1) = 3.
20. xy′+ y = x2 + x,	y(1) = 6.

22. xy′– y + y2(ln x+2)ln x = 0, y(1) = 1.

24. xy′– y = (x + y)ln(1 + xy ), y(1) = 0.

26. 3(xy′+ y) = xy2 , y(1) = 3.

28.(2xy – 4)dx =(y – x2+1)dy , y(0) = 1.

30.y′+ 3xy = x23 , y(1) = 1.

8.3. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям:

1. xy′′ ln x = y′, y(e) = e – 1, y′(e) = 1. 2. y′′cos4x = – sin2x, y(π) = 0, y′(π) = 2.

2xy′′ = y′, y(9) = 8,

y′(9) = 3.

y′′ = y′ln y′,

y(0) = 0,

y′(0) = 1.

y′′(x2 + 1) = 2xy′,

y(0) = 1,

y′(0) = 3.

y′′ = 1 −( y′)2 , y π

= 3, y′ π

= 1.

xy′′ = (1 + 2x2)y′,

y(1) =

+ 1, y′(1) = e .

y′′ = sin2x ,

y(0) = 2,

y′(0) = 1.

y′′ = 2 1 + y′ ,

y(0) = 5,

y′(0) = – 1.

10.

y′′+ (y′)2 = 0,

y(2) = ln(2e),

y′(2) = 0,5.

11.

x4y′′ + x3y′= 4 ,

y(1) = 1,

y′(1) = 2.

12.

2yy′′ = 1 + (y′)2,

y(0) = 1,

y′(0) = 1.

13.

x(y′′ + 1) + y′= 0,

y(1) = 1,

y′(1) = 0.

14.

y′′y3 + 9 = 0,

y(1) = 1,

y′(1) = 3.

15.

y′′ctg x + 2y′= 0,

y(π / 4 ) = 1,

y′(π / 4 ) = 0.

16.

y′′ = 8y3 ,

y(0) = 1,

y′(0) = 2.

17.

x2y′′ + xy′= 1,

y(1) = 0,

y′(1) = 1.

18.

(1 + sin x)y′′

y′cos x,

y(0) = 2, y′(0) = – 1.

19.

y′′(2y + 3) = 2(y′)2,

y(0) = – 1,

y′(0) = 1.

20.

(1 – x2)y′′ = xy′+ 2,

y(0) = 1,

y′(0) = 2.

21.

x2y′′ = (y′)2,

y(1) = 2,

y′(1) = 1.

22.

y′′ = (y′)2,

y(– 1) = 1,

y′(– 1) = – 1.

23.

y2y′′ = y′,

y(1) = – 1,

y′(1) = 1.

24.

2xy′y′′ = (y′)2 – 1,

y(2) = 2, y′(2) = 1.

25.

xy′′ + y′= 0,

y(1) = 0,

y′(1) = 1.

26.

y′′x = y′+ 1,

y(5) = 1,

y′(5) = 2.

27.

(y – 1)y′′ = 2(y′)2 ,

y(0) = 2,

y′(0) = 1.

28.

y′′(1 + e–x) = y′,

y(0) = 1,

y′(0) = 0.

29.

y′′ –

y′

= x(x – 1),

y(2) = 1, y′(2) = 1.

x −1

30. y′′ +	2x	y′= 2x, y(0) = – 1, y′(0) = 4.
	x2 + 1

8.4. Найти общее решение дифференциального уравнения:

1.	y′′ + y′– 2y = 3ex.	2. y′′ – 3y′+ 2y = xe2x.
3.	y′′ – y′= 2 – x.	4.	y′′ – 5y′+ 4y =2e4x.
5.	y′′ + y′= e –x .	6.	y′′ + y′– 2y = – 3e –2x.
7.	y′′ + 4y = 2sin 2x .	8.	y′′ + 9y = ex cos3x .
9.	y′′ – 3y′= 2 – 6x.	10.	y′′ – 2y′– 3y = 4e –x .
11.	y′′ – 4y′+ 4y = xe2x.	12.	y′′ + 2y′+ 5y = e x cos2x .
13.	y′′ – 12y′+ 36y = 2e6x .	14.	y′′ – 16y = e4x.
15.	y′′ + 4y′+ 4y = 2e –2x.	16.	y′′ + 2y′+ 2y = x cos x .
17.	y′′ – 3y′– 4y = –2e –x.	18.	y′′ + 2y′– 3y = ex.
19.	y′′ + y′= x(x + 2).	20.	y′′ + 7y′+ 12y = xe –3x.
21.	y′′ + 10y′= e –10x.	22.	y′′ – 6y′+ 5y =(1+x)ex.
23.	y′′ + 81y = sin 9x.	24.	y′′ + 8y′+ 16y = e –4xcos х.
25.	y′′ + 5y′ = 2х –1.	26.	y′′ – 2y′+ 5y = x sin 2x.
27.	y′′ – 2y′– 3y = (1–x)e –x.	28.	y′′ + 4y = xe2x.
29.	y′′ – y′– 6y = e3x.	30.	y′′ + 3y′+ 2y = 2e –x.

8.5. Найти общее решение системы дифференциальных уравнений:

= −y + 3z

= 4 y − z

= −3 y + 2z

= 2 y

= −2 y + 3z

= 5 y −6z

= y − 2z

= 4 y − z

= −y + 3z

= −3 y − 4z

= −2 y + 5z

= 2 y − 2z

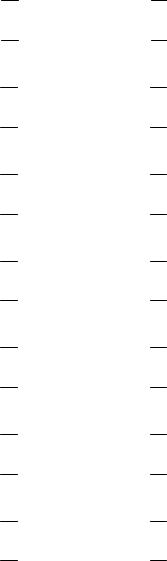
	dy = y + 2z

7.			.
	dx
	dz	= 3 y − 4z

	dx
	dy = y + 2z

10.			.
	dx
	dz		= 3 y + 2z

	dx
	dy = y + z

13.			.
	dx
	dz		= −2 y + 3z

	dx
	dy = 2 y − 4z

16.			.
	dx
	dz		= 2 y − 2z

	dx
	dy = z

19.			.
	dx
	dz		= y

	dx
	dy = 2 y + z

22.			.
	dx
	dz		= −y + 4z

	dx
	dy = y − z

25.			.
	dx
	dz		= 5 y − z

	dx

11.

14.

= −3 y + 2z

=5 y

=y − z

=−4 y + z

=4 y + z

=−2 y + z

=2 y + z

=−3 y + 2z

=−2 y + z

=−y −5z

=y + z

=y + 3z

= y − z

= y − 2z

=−3 y +6z

=−y + 8z

=y + z

=3 y + 2z

=y + 2z

=5 y + 3z

=−3 y − z

=3 y − z

=4 y − z

=y − 3z

=y + 3z

=5 y + z

= −z

dy	= y − 2z		dy	= −z	dy	= −2 y − z


		.		.		.
28. dx			29. dx		30. dx
dz	= y − z		dz	= −4 y	dz	= 4 y + 2z

dx			dx		dx

Раздел 9. РЯДЫ

Литература: [2, модуль 21-24]; [3, глава 13-15]; [4, часть 6]; [6, глава 12].

1. Числовые ряды. Основные понятия

Выражение вида

∞
a1 + a2 + ...+ an + ... = ∑an		(9.1)
n=	1

называется числовым рядом или просто рядом. При этом числа a1, a2, ... , an, ...

называются членами ряда, а член an с произвольным номером n – его общим чле-

ном или n-членом.

Нумерацию слагаемых можно начинать не с единицы, а с любого целого чис-

∞	∞	∞
ла. Например, ∑2n−1 ,	∑2n ,	∑ 2n+1 и т. п. – это запись одного и того же
n=1	n=0	n=−1

ряда 1 + 2 + 4 + 8 + 16 + ...

Ряд считается заданным, если задан его общий член. Обычно общий член ряда

задаётся функцией, зависящей от номера n: an = f (n) . Полагая в нём n = 1, 2, ...

, можно найти любой член этого ряда.

Например, если общий член ряда имеет вид an =		n	, то
	n2	+ ( −1 )n+1

a1 =				1			=	1	,	a2 =	2		=		2	, a3 =				3		=	3	, ...
a1 =		12 + ( −1 )1+1					=	2	,	a2 =	22 + ( −1 )2+1		=	3		, a3 =			32 + ( −1 )3+1			=	10	, ...
		12 + ( −1 )1+1						2			22 + ( −1 )2+1			3					32 + ( −1 )3+1				10
Ряд, составленный из этих членов, будет иметь вид
	1		2		3					n					∞				n
	1	+	2	+	3	+ ...+				n		+ ... или		∑					n		.
2		+		+		+ ...+		n	2		n+1	+ ... или		∑			2			n+1	.
2		3		10				n		+ ( −1 )				n=1 n				+ ( −1 )

Понятие суммы ряда определяется с помощью предельного перехода. Для этого рассмотрим сумму первых n членов ряда (9.1)

n
Sn = a1 + a2 + ...+ an = ∑ai ,	(9.2)

i=1

называемую n-й частичной суммой этого ряда. Ясно, что первая, вторая, третья и т. д. частичные суммы

S1 = a1, S2 = a1 + a2, S3 = a1 + a2 + a3 , ...

будут обычными суммами конечного числа слагаемых, они образуют бесконечную последовательность.

Если эта последовательность имеет конечный предел

S = lim Sn ,	(9.3)
n→∞

то этот предел называется суммой ряда, а сам ряд называется сходящимся.

Если же предел частичных сумм не существует или равен ∞, то говорят, что ряд суммы не имеет и его называют расходящимся.

Основные задачи теории числовых рядов:

1)установить, будет ли данный ряд сходящимся или расходящимся (проверка ряда на сходимость);

2)найти сумму сходящегося ряда (суммирование ряда).

Иногда сумму ряда можно вычислить непосредственно, исходя из определения. Рассмотрим примеры.

Пример 9.1. Исследовать ряд, составленный из членов геометрической про-

		∞
грессии a + aq + aq2	+ ...+ aqn−1	+ ... = ∑aqn−1 , a ≠ 0.
		n=	1

Решение. Рассмотрим частичную сумму: Sn = a + aq + aq2 + ...+ aqn−1 . Ум-

ножим обе части этого равенства на q, а затем вычтем одно равенство из другого:

Snq = aq + aq2 + ...+ aqn , Sn − Snq = a − aqn .

Отсюда находим Sn

= a

1 − qn

. При нахождении

lim Sn

рассмотрим случаи.

− q

n→∞

1) Пусть |q| < 1, тогда

lim qn = 0,

lim Sn

, поэтому ряд сходится и

− q

n→∞

его сумма равна S =

1 − q

2) Пусть |q| > 1, тогда

lim qn = ∞,

lim Sn = ∞ , ряд расходится.

n→∞

3) При q = 1 имеем Sn = an, поэтому

lim Sn = ∞ , ряд расходится.

n→∞

4) При q = –1 последовательность частичных сумм имеет вид a, 0, a, 0, ... Та-

кая последовательность предела не имеет, поэтому ряд расходится.

∞

Итак, ряд ∑aqn−1

сходится при |q| < 1 и при этом его сумма S =

, а

− q

n=1

при |q| ≥ 1 данный ряд расходится.

Пример 9. 2.

Исследовать ряд

∞

...+

+ ... = ∑

1 2

2 3

n( n + 1 )

n=1 n( n + 1 )

Решение. Вначале разложим правильную дробь на сумму простейших дробей:

A( n + 1 ) + Bn

A( n + 1 ) + Bn ≡ 1

n( n + 1 )

n +

n( n + 1 )

( A + B )n + A ≡ 1 A + B = 0 , A = 1 A = 1, B = −1.

Итак,

−

n( n +

1 )

n + 1

Частичную сумму можно представить так:

+...+

1−

−

+...+

−

1 2 2 3 3 4

n(n+1)

2 3 3 4

n n+1

Заметив, что все слагаемые, кроме первого и последнего, сокращаются, полу-

Sn = 1 −

чим

. Так как

lim Sn =

lim

−

= 1 , поэтому ряд сходится

n→∞

n + 1

и его сумма равна 1.

Рассмотрим основные свойства рядов.

Свойство 1. Если ряд с общим членом an сходится, то

lim an = 0 .

(9.4)

n→∞

Этот результат называется необходимым признаком сходимости ряда, так как если ряд сходится, то указанный результат обязательно имеет место.

Очевидно, что при нарушении условия (9.4) соответствующий ряд обязательно будет расходящимся.

∞	n					n
Например, ряд ∑	n		расходится, так как	lim an = lim		n		= 1	≠ 0	; так-
Например, ряд ∑		2	расходится, так как	lim an = lim				= 1	≠ 0	; так-
n=1 n +		2		n→∞	n→∞ n +		2
	∞
же расходится и ряд ∑( −1 )n , так как lim an = lim ( −1 )n не существует.
n=1			n→∞	n→∞
n=1

Обратим внимание на следующее обстоятельство. Условию (9.4) удовлетворяют не только сходящиеся ряды, но и некоторые расходящиеся ряды. Если равенство (9.4) выполняется, то соответствующий ряд не обязательно будет сходящимся, он может оказаться и расходящимся. Поэтому условие (9.4) не является достаточным условием сходимости ряда.

∞	1
Пример 9.3. Исследовать ряд ∑	1	.
Пример 9.3. Исследовать ряд ∑	n	.
n=1	n
Решение. Частичная сумма Sn =	1	+	1	+ ...+	1	≥ n	1	= n . Из тео-
Решение. Частичная сумма Sn =	1	+	2	+ ...+	n	≥ n	n	= n . Из тео-
	1		2		n		n

рии пределов следует, что lim Sn ≥ lim n = ∞ .			Следовательно, рассматривае-
n→∞	n→∞		1
мый ряд расходящийся, хотя условие lim an = lim			1	= 0 выполнено.
мый ряд расходящийся, хотя условие lim an = lim				= 0 выполнено.
	n→∞	n→∞	n
∞				∞
Свойство 2. Если ряд ∑an	сходится и его сумма равна S, то ряд ∑can ,
n=1				n=1
где с – произвольное число, также сходится и его сумма равна сS.
	∞			∞
Очевидно, что если исходный ряд ∑an		расходящийся, то и ряд ∑can бу-
дет расходиться при с ≠ 0.	n=1			n=1
дет расходиться при с ≠ 0.
	∞	∞
Свойство 3. Если сходятся ряды ∑an		и ∑bn , а их суммы равны S(a) и
	n=1	n=1

	∞
S(b)	соответственно, то сходятся и ряды ∑(an ± bn ) , причём сумма каждого
	n=	1

равна S(a) ± S(b) соответственно.

Замечания. 1) Нетрудно убедиться, что сумма (разность) сходящегося и расходящегося рядов есть расходящийся ряд, а сумма (разность) двух расходящихся рядов может быть как сходящимся, так и расходящимся рядом.

2) Сходимость ряда не зависит от первых членов, а определяется поведением слагаемых an при n → ∞ . Изучая сходимость ряда, можно номер n брать любым натуральным числом.

2. Достаточные признаки сходимости знакоположительных рядов

Рассмотрим некоторые достаточные условия сходимости знакоположительных рядов, т. е. рядов с неотрицательными членами.

Поведение частичной суммы Sn знакоположительного ряда особенно простое: Sn монотонно возрастает при возрастании n, так как при возрастании n каждый новый член ряда, попадающий в Sn, положителен. Если такая последовательность Sn ограничена сверху, то, как следует из теории пределов, будет существовать

конечный lim Sn и, следовательно, ряд будет сходиться.

n→∞

Таким образом, для установления сходимости знакоположительного ряда достаточно установить ограниченность сверху всех его частичных сумм. Этот резуль-

тат и является общим достаточным критерием сходимости знакоположительных рядов.

Если же последовательность частичных сумм не ограничена сверху, то ряд будет расходиться.

На практике более удобными критериями сходимости являются так называемые достаточные признаки сходимости. Ограничимся формулировкой основных таких признаков: интегрального признака; двух признаков, основанных на сравнении рядов; признака Даламбера и признака Коши.

2.1. Интегральный признак.

∞

Пусть дан знакоположительный ряд ∑an , члены которого являются зна-

n=1

чениями некоторой функции f(x) при x = n, т. е. an = f(n), где f(x) – положительная, непрерывная и монотонно убывающая функция на [1; +∞). Тогда, если

+∞	∞
несобственный интеграл ∫	f ( x )dx сходится, то сходится и ряд ∑an ; если
1	n=1
+∞	∞
же ∫ f ( x )dx расходится, то ряд ∑an также расходится.
1	n=1

+∞

Напомним, что несобственный интеграл ∫ f ( x )dx называется сходящимся,

	1
	a
если существует конечный предел lim	∫ f ( x )dx.
a→+∞	1
	1

∞

Пример 9.4. Исследовать на сходимость ряд ∑

n=2

n ln3 n .

Решение. Применим интегральный признак. Для этого рассмотрим функцию

f ( x ) =	1		. Имеем f(n) = an. При возрастании х оба сомножителя в знаме-
	x ln3
		x

нателе функции f(x) монотонно возрастают, поэтому f(x) монотонно убывает. Далее, x [2, +∞) f(x) > 0. Вычислим интеграл

+∞

−3

∫

dx =

lim

∫(ln x)

d (ln x) =

lim

−

x ln

a→+∞

2 ln

lim

−

2 ln

a→+∞

Итак, несобственный интеграл сходится, поэтому, согласно интегральному признаку, данный ряд сходится.

Рассмотрим применение интегрального признака сходимости для ряда

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 169 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.08.201988.04 Кб1Zadacha_1_5-7.docx
#
14.02.2015193.02 Кб31ZADAChI_1.doc
#
14.02.2015134.14 Кб66ZADAChI_V.doc
#
14.02.2015866.93 Кб199zadat-fkh.pdf
#
14.02.201515.12 Mб32zaginajlov-kvl.pdf
#
14.02.20151.33 Mб24zaicevVM_2.pdf
#
14.02.20151.25 Mб29zajcevVM.pdf
#
12.03.2016345.72 Кб28zarnitsina-e-g-mapp-549003aae0d37.pdf
#
14.02.20154.64 Mб56zarn_met_kp.pdf
#
14.02.2015527.89 Кб23zarn_met_lab.pdf
#
14.02.20152.32 Mб8Zaschita_ot_shuma_404.doc