
zaicevVM_2
.pdf
∑∞ n + 1 n
10. . n=1 n + 2
∑∞ 2n2 +n n
13. . n=1 10n2 −1
∞ 6n+1
16. n∑=1 ( 2n + 1 )! .
∑∞ 2n + 1 3n
19. .
n=1 2n −1
22. ∑∞ ( n + 1 )! .
n=1 n10
11. ∑∞ nn .
n=1 n!
14. ∑∞ ( 2n )! . n=1 ( n + 1 )!
∞ |
1 + 2n |
2n |
|||
17. ∑ |
|
|
|
|
. |
|
2 |
+ 3 |
|||
n=1 |
n |
|
|
||
20. ∑∞ n2 + 1 . n=1 ( n + 2 )!
∑∞ 4n − 3 n2
23. . n=1 5n + 1
∞ |
|
|
n + 1 |
|
n |
∞ |
|
|
1 |
|
|
|
|
|
25. ∑ |
|
|
∑ |
|
|
|
|
|
|
|
||||
3 n |
|
|
|
. 26. |
|
|
|
|
. |
|
|
|
||
2n + 1 |
|
|
|
n |
|
|
|
|||||||
n=1 |
|
|
|
n=1 n! 2 |
|
|
|
|
|
|||||
∞ |
3n n2 |
|
|
∞ |
|
2n −1 |
n |
|||||||
|
|
2 |
|
|||||||||||
28. ∑ |
|
|
. |
|
29. |
∑ |
|
|
|
|
. |
|||
n! |
|
|
3n + 1 |
|||||||||||
n=1 |
|
|
|
|
n=1 |
|
|
|
|
|||||
∞ |
|
|
|
7 n + 1 |
n |
|
12. ∑ |
|
1 |
+ |
|
|
. |
|
2n −1 |
|||||
n=1 |
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
||
15. ∑ 2n −1 (0,2)2−n . |
|||||||||||||
n=1 |
|
|
|
|
|
|
|
|
|
|
|
||
∞ |
( 2n −1 )! |
|
|||||||||||
18. ∑ |
. |
||||||||||||
|
|
|
|
||||||||||
n=1 |
|
( n + 1 )! |
|||||||||||
∞ |
|
|
2 |
3−n |
|
|
|
|
|
||||
21. ∑ |
|
|
|
|
|
. |
|
|
|
||||
|
2n + |
1 |
|
|
|
||||||||
n=1 |
|
|
|
|
|
|
|||||||
∞ |
|
|
|
n |
2 |
|
|
|
|
|
|
||
24. ∑ |
|
|
|
|
|
|
|
. |
|
|
|||
( n + 2 )! |
|
||||||||||||
n=1 |
|
|
|
||||||||||
∞ |
|
2n + 1 |
|
|
|
|
|||||||
27. ∑ |
|
. |
|
|
|
||||||||
|
|
|
|
|
|||||||||
n=1 |
|
|
n 2n |
|
|
|
|
|
|||||
∞ |
4 |
n |
( n |
+ 1 ) |
|
|
|||||||
30. ∑ |
|
|
. |
||||||||||
|
|
|
|
|
|
|
|||||||
n=1 |
|
|
|
n! |
|
|
|
|
|
||||
9.2. Найти интервал сходимости степенного ряда и исследовать сходимость на концах интервала сходимости.
|
∞ |
n + 1 |
n2 |
|
n |
|
|
|||||||
1. |
∑ |
|
|
|
|
|
x |
|
|
. |
|
|||
|
|
n |
|
|
||||||||||
|
n= |
1 |
|
|
|
|
|
|
|
|||||
|
∞ |
|
|
n |
|
|
|
|
1 |
|
|
|||
|
∑x |
|
|
|
|
|
||||||||
4. |
|
ln |
1 + |
|
|
. |
||||||||
|
n |
|||||||||||||
|
n= |
1 |
|
|
|
|
|
|
|
|
|
|||
|
∞ |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
7. |
∑nxn sin |
. |
|
|
|
|
||||||||
|
|
|
|
|
||||||||||
|
n= |
1 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
n |
|
10. |
∑(−1)n |
( x + 1 ) |
. |
|||||||||||
|
||||||||||||||
|
n= |
1 |
|
|
|
|
|
n + 5 |
|
|
||||
|
∞ |
|
|
|
n n2 ( x − 4 )n |
|||||||||
13. |
∑( −1 ) |
|
|
|
|
|
|
|
|
|||||
|
|
|
e |
n |
|
|
||||||||
|
n= |
1 |
|
|
|
|
|
|
|
|
|
|
||
|
∞ |
|
n2 |
|
|
|
|
|
|
|
|
|
n |
||||
2. |
∑ |
|
|
|
|
|
|
|
( x − |
3 ) . |
|||||||
n |
2 |
+ 1 |
|
||||||||||||||
|
n=1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
∞ |
( x −5 )n |
|
|
|
|
|
||||||||||
5. ∑ |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|||
|
n + 2 |
n |
|
|
|
||||||||||||
|
n=1 |
|
|
|
|
|
|
|
|
|
|||||||
|
∞ |
n( x + |
|
|
n |
|
|
|
|||||||||
8. |
∑ |
|
2 ) |
|
. |
|
|
||||||||||
|
|
n |
|
|
|
|
|
||||||||||
|
n=1 |
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
n |
|
|
n |
xn |
||||||||
11. |
∑ |
|
|
|
|
|
|
|
|
|
|
|
. |
||||
|
|
+ 1 |
|
4 |
n |
||||||||||||
|
n=1 |
n |
|
|
|
|
|||||||||||
|
∞ |
|
|
|
|
1 |
n |
|
|
|
|||||||
. 14. |
∑tg |
|
|
|
|
|
x |
|
|
. |
|
||||||
|
|
2 |
|
|
|
|
|||||||||||
|
n=1 |
|
|
n |
|
|
|
|
|
|
|
|
|||||
|
∞ |
|
|
|
|
|
|
n |
|
|
|
|
||
3. |
∑ |
( x − 2 ) |
. |
|
|
|
||||||||
|
|
n |
|
|
|
|||||||||
|
n=1 |
|
|
|
n3 |
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
n |
|
|
|
||
6. ∑(−1)n |
|
|
|
|
( x + 1 )n . |
|||||||||
|
n + |
1 |
||||||||||||
|
n=1 |
|
|
|
|
|
|
|
||||||
|
∞ |
|
5 |
n |
( x |
|
|
|
|
n |
|
|||
9. |
∑ |
|
+ 3 ) |
. |
|
|||||||||
|
|
|
|
|
|
|
|
|||||||
|
n=1 |
|
|
|
|
n + 3 |
|
|
|
|
||||
|
∞ |
|
|
|
|
n |
|
2nxn |
|
|||||
12. |
∑( |
−1 ) |
|
|
|
|
|
|
|
. |
||||
|
n |
3 |
|
+ |
2 |
|||||||||
|
n=1 |
|
|
|
|
|
|
|
|
|
||||
|
∞ |
|
2n + 1 n |
|
|
n |
||||||||
15. |
∑ |
|
|
|
|
|
|
( x + 2 ) . |
||||||
|
|
n |
|
|
||||||||||
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|||
118
|
∞ |
|
|
n |
|
|
1 |
|
|
|
|
|
∞ |
( x − 3 )n |
|
|
|
|
|
|
|
|
∞ 2n |
|
n |
|
|
|
|
|
n |
|||||||||||||||||||
16. |
∑x |
|
ln( 1 + |
|
|
|
|
|
). |
17. |
∑ |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
18. |
∑ |
|
|
|
|
|
|
|
( x + 1 ) . |
|||||||||||||||
|
n |
2 |
|
( n + |
3 )5 |
n−1 |
|
|
|
3n + |
5 |
|
||||||||||||||||||||||||||||||||||||||
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
∞ |
|
( x +6 )n |
|
|
|
|
|
|
|
|
∞ |
|
|
n |
|
|
nxn |
|
|
|
|
∞ |
|
|
|
n+1 nxn |
|
|
|||||||||||||||||||||
19. |
∑ |
|
|
|
|
|
|
|
. |
|
|
20. ∑( −1 ) |
|
|
|
|
|
|
|
|
|
. |
|
|
21. ∑( −1 ) |
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||
|
|
2 |
+ 2n + |
3 |
|
|
|
( n + |
2 |
|
|
|
|
|
|
3 |
+ |
1 |
||||||||||||||||||||||||||||||||
|
n=1 n |
|
|
|
|
|
|
|
n=1 |
|
|
|
|
1 ) |
|
|
|
|
n=1 |
|
|
|
|
|
|
n |
|
|||||||||||||||||||||||
|
∞ |
(x + 1,5)n |
|
|
|
|
|
|
∞ |
3n ( x − 2 )n |
|
|
|
|
|
|
|
|
∞ |
|
|
|
n |
|
|
n |
|
|
|
|
|
n |
||||||||||||||||||
22. |
∑ |
|
|
|
n |
|
. |
|
|
|
|
23. |
∑ |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
24. |
∑ |
|
|
|
|
|
|
|
( x + 2 ) . |
|||||||||||||
|
|
2 |
+ 5n |
|
|
|
|
3n + 1 |
|
|
|
|
|
|
3n + 1 |
|
||||||||||||||||||||||||||||||||||
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
∞ |
|
|
|
|
n |
2 |
n |
|
∞ |
5 |
n |
x |
n |
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
|
2 |
( x |
+ 5 |
|
n |
|
|
|
|||||||||||||
25. |
∑ |
( x + 4 ) |
|
|
. |
26. |
∑ |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
27. |
∑ |
n |
|
) |
. |
|
|
|||||||||||||||||||||
n |
|
|
|
|
|
n |
+ n |
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
||||||||||||||||||||||||
|
n=1 |
|
|
|
2 + n |
|
|
|
|
|
|
|
|
n=1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
n=1 ( n + 1 ) |
|
|
|
|
|
|
||||||||||||||||
|
∞ |
|
n |
|
n |
|
1 −n |
|
∞ |
|
|
n |
|
|
|
n2 n |
n |
|
|
∞ |
|
|
|
n |
|
|
n |
|
|
|
|
|
n |
|||||||||||||||||
28. |
∑ |
2 |
|
|
x |
1 + |
|
|
|
|
. |
29. ∑( −1 ) |
|
|
|
|
|
|
|
|
|
x |
|
. |
30. ∑( −1 ) |
|
|
|
|
|
|
|
( x +1 ) . |
|||||||||||||||||
|
|
|
n |
|
|
2 |
+ |
|
|
|
|
n |
3 |
+ |
1 |
|||||||||||||||||||||||||||||||||||
|
n=1 |
|
|
|
|
|
|
|
|
n=1 |
|
|
|
n |
|
1 |
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
9.3. Вычислить определённый интеграл с точностью до 0,001, разложив подынтегральную функцию в ряд Маклорена и затем проинтегрировав его почленно.
|
0 ,1 |
|
|
|
1. |
∫ e−5 x2 dx . |
|||
|
0 |
|
|
|
|
0 ,5 |
|
|
|
4. |
∫ 3 1 + x2 dx . |
|||
|
0 |
|
|
|
|
1 |
− |
x2 |
|
7. |
∫e |
|
dx . |
|
2 |
||||
|
0 |
|
|
|
0,5
10.∫ arctg (x2 ) dx .
0
0,5
13.∫ ln(1 + x3 ) dx .
0 |
|
|
|
0 ,8 |
dx |
|
|
16. ∫ |
|
. |
|
1 + x |
5 |
||
0 |
|
|
19. ∫1 x2 sin(x2 ) dx .
0
|
0 ,8 |
|
|
(2 x2 ) dx . |
||||
2. |
∫ cos |
|||||||
|
0 |
|
|
|
|
|
|
|
|
0 ,6 |
|
dx |
|
|
|
||
5. |
∫ |
|
|
|
|
. |
||
|
1 + x |
3 |
||||||
|
0 |
|
|
|
||||
|
1 |
|
|
( |
|
|
|
|
8. |
∫ |
sin |
x2 |
|
dx . |
|||
|
|
|
|
) |
|
|||
|
0 |
|
|
|
|
|
|
|
0,5
11.∫ x ln(1 + x2 ) dx .
|
0 |
|
|
|
0 ,8 |
|
|
14. |
∫ |
1 + x3 dx . |
|
|
0 |
|
|
|
0 ,4 |
e− |
3 x2 |
17. |
∫ |
4 dx . |
|
|
0 |
|
|
0,8
20.∫ x2 ln(1 + x)dx .
0
0 ,5
3. ∫ 3 1 + x3 dx .
0
0,5
6.∫ x arc tgx dx .
0
0 ,5
9. ∫ 1 + x2dx .
0
12. ∫1 cos (x2 ) dx .
0
0,6
15.∫ sin(2 x2 )dx .
0
18. |
∫1 |
|
|
|
|
dx |
|
|
. |
|
3 |
|
3 |
|
|
||||
|
0 |
|
|
|
x |
+64 |
|
||
|
0 ,5 |
|
|
dx |
|
|
|
||
21. |
∫ |
|
|
|
. |
|
|||
|
1 + x |
4 |
|
||||||
|
0 |
|
|
|
|
|
|||
119
|
1 |
|
|
|
( |
|
|
22. |
∫ |
x2 |
cos |
x2 |
dx . |
||
|
|
|
|
|
) |
||
|
0 |
|
|
|
|
|
|
|
0 ,5 |
|
3 x2 |
|
|
|
|
25. |
∫ e |
− 25 dx . |
|
||||
|
0 |
|
|
|
|
|
|
28. |
∫1 arctg (x3 ) dx . |
||||||
|
0 |
|
|
|
|
|
|
0 ,5 |
x |
|
|
23. ∫ |
|
dx . |
|
1 + x |
5 |
||
0 |
|
|
0,5
26.∫ sin(4 x2 )dx .
0 |
|
|
|
|
0 ,5 |
x |
2 |
|
|
29. ∫ |
|
|
dx . |
|
16 + x |
4 |
|||
0 |
|
|
||
|
1,5 |
|
|
|
dx |
|
|
|
|
|
|
24. |
∫ |
|
|
|
|
|
. |
||||
4 |
x |
4 |
|
|
|
||||||
|
0 |
|
|
|
+ 81 |
|
|
|
|||
|
2 ,5 |
|
|
|
|
dx |
|
|
|
|
|
27. |
∫ |
|
|
|
|
|
|
. |
|||
|
3 |
125 + x |
3 |
||||||||
|
0 |
|
|
|
|
|
|
||||
|
0 ,5 |
|
|
|
dx |
|
|
|
|
|
|
30. |
∫ |
|
|
|
. |
|
|
|
|||
|
|
1 + x |
4 |
|
|
|
|||||
|
0 |
|
|
|
|
|
|
|
|
||
9.4. Найти три первых отличных от нуля члена разложения в степенной ряд решения y = y( x ) указанной задачи Коши.
1. |
y′ = e x + y2 , y (0) = 1 . |
|||||
3. |
|
y′ = cos x + y2 , |
y (0) = 1 . |
|||
5. |
y′ = x2 + y2 , y (0) = 2 |
|||||
7. |
y′ = x2 + y2 − x, y (0) = 3 . |
|||||
9. |
|
y′ = 2cos x − xy2 , |
y (0) = 1 . |
|||
11. |
y′ = |
x2 + y2 , |
|
y (0) = 4 . |
||
13. |
y′ = x arctgx + y2 , |
y (0) = 2 . |
||||
15. |
y′ = ln(1 + x) + y2 , |
y (0) = 0 . |
||||
17. |
y′ = x2 + y2 + 2 x, |
y (0) = −1 . |
||||
19. |
y′ = |
1 + xy , |
y (0) = 1 . |
|||
21. |
y′ = xy2 − x − 1, |
y (0) = 0 . |
||||
23. |
y′ = x ln y − e−x , |
y (0) = 1 . |
||||
25. |
y′ = x2 + y2 − x, |
y (0) = 3 . |
||||
27. |
y′ = |
2 x + y2 , |
|
y (0) = 4 . |
||
29. |
y′ = e− y − x, |
y (0) = 0 . |
||||
2. y′ = 2e y + y, y (0) = 0 .
4. |
y′ = sin x + y2 , |
y (0) = 1 . |
||
6. |
y′ = 2e y − xy, |
|
y (0) = 0 . |
|
8. y′ = 2 xy + y2 + 1, y (0) = 4 . |
||||
10. |
y′ = xe y + y2 , |
y (0) = 1 . |
||
12. |
y′ = x sin x + y3 , |
y (0) = 1 . |
||
14. |
y′ = x + y2 , |
y (0) = 3 . |
||
16. |
y′ = xy + cos y, |
y (0) = 0 . |
||
18. |
y′ = x2 − y2 + 1, |
y (0) = 2 . |
||
20. |
y′ = x + y2 |
+ 2, |
y (0) = 1 . |
|
22. |
y′ = xy3 + 3, |
|
y (0) = −1 . |
|
24. |
y′ = x cos x + e2 y , |
y (0) = 0 . |
||
26. |
y′ = ( x2 + y)2 , |
y (0) = 1 . |
||
28. |
y′ = x3 + 2 y2 , |
y (0) = −2 . |
||
30. |
y′ = ln( x2 + y) + 1, y (0) = 1 . |
|||
120
|
9.5. Разложить функцию f(x) в ряд Фурье на указанном промежутке. |
|
|
|
|
|
|||||||||||||||
1. |
f(x) = 5 – x, |
[0; 3], |
по синусам. |
|
2. f(x) = 2x – 1, |
[– 2; 2]. |
|
|
|||||||||||||
3. |
2 x |
, 0 ≤ x < 1 |
, по косинусам. |
4. |
f(x) = – 3x + 1, |
[– π ; π]. |
|
||||||||||||||
f(x) = |
, |
1 |
≤ x ≤ 2 |
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
5. f(x) = 1 + 2x, |
[0; 2], по синусам. |
6. |
f(x) = 1 – x, |
[– 0,5; 0,5]. |
|||||||||||||||||
|
2( 1 − x ) , 0 |
≤ x < 2 |
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
||||||
7. f(x) = |
|
|
|
|
|
|
|
, по косинусам. |
8. |
f(x) = 3x, [– |
|
; |
|
|
]. |
|
|
||||
|
−2 |
|
|
, 2 ≤ x ≤ 3 |
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|||
9. f(x) = 4x – 1, |
[0; 1], по синусам. |
|
10. |
f(x) = 9 + 2x, |
[– |
π |
; |
π |
]. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
||
11. |
|
|
1, |
|
0 ≤ x < 1 |
, по косинусам. |
12. |
f(x) = x + 5, |
|
[–1; 1]. |
|
||||||||||
f(x) = |
|
|
− x ), 1 ≤ x ≤ |
3 |
|
|
|||||||||||||||
|
0,5( 3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
13. |
f(x) = 1 – 3x, |
[0; 4], по синусам. |
14. f(x) = 9x – 2, |
[– 3; 3]. |
|
||||||||||||||||
15. |
x −1, |
0 ≤ x < 2 |
, по косинусам. |
16. |
f(x) = – 2x, |
[– 1; 1]. |
|
|
|||||||||||||
f(x) = |
1 |
, |
2 ≤ x ≤ 4 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
17. |
f(x) = 2x + 3, |
[0; 0,5], по синусам. |
18. f(x) = 2x – 3, |
[– 4; 4]. |
|
||||||||||||||||
|
|
−2, |
|
0 ≤ x < 1 |
, по косинусам. |
20. f(x) = 4 – 5x, |
[– 2; 2]. |
|
|||||||||||||
19. f(x) = |
|
− 2 ), 1 ≤ x ≤ |
2 |
|
|
||||||||||||||||
|
2( x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
21. |
f(x) = 2 – 3x, [0; 1], по синусам. |
22. f(x) = 1 – 2x, |
[– 2; 2]. |
|
|||||||||||||||||
23. |
3, |
|
0 ≤ x < 2 |
, по косинусам. |
24. |
f(x) = x – 4, |
[– 1; 1]. |
|
|
||||||||||||
f(x) = |
− 2x, 2 ≤ x ≤ 3 |
|
|
||||||||||||||||||
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
25. |
f(x) = 3 – 2x, |
[0; 2], по синусам. |
26. |
f(x) = 2x – 5, |
[– 3; 3]. |
|
|||||||||||||||
27. |
2, |
|
0 ≤ x < 1 |
, по косинусам. |
28. |
f(x) = 4 – x, |
[– 4; 4]. |
|
|
||||||||||||
f(x) = |
− 2 x, 1 ≤ x ≤ 3 |
|
|
||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
29. |
f(x) = 3 + 4x, |
[0; 3], по синусам. |
30. |
f(x) = 2x + 3, |
[– 2; 2]. |
|
|||||||||||||||
121
Раздел 10. ОПРЕДЕЛЁННЫЕ ИНТЕГРАЛЫ ПО ФИГУРАМ
Литература: [1, модуль 16]; [3, глава 11,12]; ]; [4, часть 5]; [6, глава 8].
В разделе 7 было рассмотрено понятие определённого интеграла от функции f(x), заданной на отрезке [a, b] числовой оси. Изложенная схема построения определённого интеграла на отрезке [a, b] (составление интегральных сумм, предельный переход) и его основные свойства могут быть применены для функции, заданной на фигуре. В зависимости от вида фигуры будут получены соответствующие типы определённых интегралов.
1.Понятие определённого интеграла по фигуре
1.1Фигура. Мера. Плотность массы.
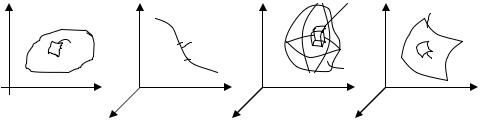
Будем называть фигурой либо плоскую область D (рисунок 1), либо линию L в пространстве или на плоскости (рисунок 2), либо пространственное тело T (рисунок 3), либо поверхность Σ в пространстве (рисунок 4).
y |
z |
L |
(∆Vi) |
z |
Σ |
|
z |
||||||
|
|
|||||
Mi ● (∆Si ) |
(∆Li ) |
Mi● |
|
|
||
Mi ● |
T |
|
Mi ● (∆σi ) |
|||
D |
|
|
0 |
|
||
|
0 |
|
0 |
y |
||
0 |
x |
y |
y |
x |
||
Рисунок 1 |
x |
Рисунок 2 |
x Рисунок 3 |
Рисунок 4 |
||
Пусть E – общее обозначение всех четырёх рассматриваемых фигур. Диаметром d(E) фигуры E будем называть максимальное из расстояний ме-
жду двумя точками этой фигуры. В основном будут рассматриваться только фигуры конечного диаметра (ограниченные фигуры).
Будем считать, что каждая фигура имеет меру S(E) (площадь для D и Σ, длину для L, объём для T). Строгие определения для площади, длины, объёма в данном пособии не приводятся.
Во многих механических приложениях каждая рассматриваемая фигура E предполагается материальной, т. е. на ней распределена масса вещества с плотностью ρ = f(M), где M – любая текущая точка фигуры E, а f(M) непрерывная функция.
Если плотность постоянная во всех точках фигуры E, т. е. ρ = f(M) = const, то фигуру называют однородной.
121
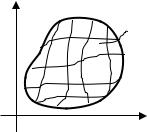
1.2. Задача о массе фигуры.
Рассмотрим задачу: пусть в каждой точке M фигуры E известна её плотность ρ = f(M), нужно найти массу этой фигуры.
y |
Решим эту задачу вначале для случая, когда |
|
фигура – плоская область D. |
||
(∆Si) |
||
|
Для этого разобьём произвольным образом эту |
|
Mi ● |
фигуру на n частей: (∆S1 ), (∆S2 ), ... , (∆Sn ), где |
|
|
(∆Si ) (i = 1, 2, ... , n) обозначает i - ю часть раз- |
Dбиения. Площадь этой части будем обозначать ∆Si (рисунок 5).
O |
x |
На каждой i-й части (∆Si ) возьмём произ- |
Рисунок 5 |
вольную точку Mi. Приближённо считаем, что во |
|
|
всех |
точках части (∆Si ) плотность постоянна и |
равна f(Mi ). Тогда для массы m(D) фигуры D получается приближённое равенство
n |
|
m( D ) ≈ ∑ f ( Mi )∆Si . |
(10.1) |
i=1
Написанное приближённое равенство будет тем точнее, чем меньше будут размеры
частей (∆Si ), на которые разбита фигура D. Пусть d = max d( ∆Si ) – наибольший |
|
i |
|
из диаметров частей, тогда масса фигуры D будет иметь точное выражение |
|
n |
|
m( D ) = lim ∑ f ( Mi )∆Si . |
(10.1′) |
d →0 i=1 |
|
Для остальных фигур задача о массе решается совершенно аналогично, поэтому решение приведём совсем кратко.
В случае фигуры L (рисунок 2) разбиваем ее на части (∆Li ) длиной ∆Li
(i = 1, …, n), выбираем на каждой части (∆Li ) произвольно точку Mi и получаем для массы приближенное равенство
n |
|
m( L ) ≈ ∑ f ( Mi )∆Li |
(10.2) |
i=1 |
|
и точное равенство |
|
n |
|
m( L ) = lim ∑ f ( Mi )∆Li , |
(10.2′) |
d →0 i=1 |
|
где d – максимальный из диаметров частей (∆Li ). |
|
В случае фигуры T получаем (обозначения ясны из рисунка 3): |
|
n |
|
m(T ) ≈ ∑ f ( Mi )∆Vi , |
(10.3) |
i=1
122
n |
|
m(T ) = lim ∑ f ( Mi )∆Vi . |
(10.3′) |
d →0 i=1 |
|
Здесь d – наибольший из диаметров частей (∆Vi ) c объемом ∆Vi. |
|
В случае фигуры Σ поступаем таким же образом (см. рисунок 4): |
|
n |
|
m( Σ ) ≈ ∑ f ( Mi )∆σi , |
(10.4) |
i=1 |
|
n |
|
m( Σ ) = lim ∑ f ( Mi )∆σi , |
(10.4′) |
d →0 i=1 |
|
где d – наибольший из диаметров частей (∆σi ) площадью ∆σi.
Итак, чтобы найти массу фигур, нужно вычислить однотипные пределы
(10.1′) – (10.4′).
1.3. Интегральная сумма и определённый интеграл по фигуре.
Отвлечёмся от физического смысла рассмотренной задачи о массе фигуры E и перечислим те математические операции, которые привели к её решению.
Пусть теперь F(M)–произвольная функция, заданная в каждой точке M фигуры E. Для получения приближённых равенств были проделаны следующие операции:
1)фигура E произвольным образом разбивалась на n частей (∆Ei ), i =1,…,n, мерой ∆Ei каждая;
2)на каждой части (∆Ei ) бралась произвольная точка Mi и вычислялось значение функции f(Mi ) в этой точке;
3)значение f(Mi ) умножалось на меру ∆Ei соответствующей части (∆Ei );
4)составлялась сумма таких произведений.
Полученная в результате перечисленных операций сумма
n |
|
∑ f ( Mi )∆Ei |
(10.5) |
i=1
называется интегральной суммой для функции f(M) по фигуре E. Для рассматриваемых фигур интегральные суммы записаны в правых частях выражений (10.1) – (10.4).
Замечание. При заданном числе n можно составить сколько угодно интегральных сумм, так как можно разными способами разбивать фигуру на части и на каждой части можно произвольным образом выбирать точку Mi.
При решении задачи о массе мы делали ещё одну операцию – рассматривали предел интегральной суммы при стремлении к нулю размеров частей, на которые
была разбита фигура (при этом, конечно, число частей n→∞). Важно заметить, что этот предел (в задаче о массе − это масса фигуры) не должен зависеть от способа
123
разбиения и способа выбора точек (т. е. от способа составления интегральной суммы).
Определённым интегралом по фигуре E от заданной на ней функции f(M) называется предел интегральной суммы, когда стремится к нулю наибольший из диаметров d частей, на которые разбивается фигура при составлении интегральных сумм. При этом предел не должен зависеть от способа составления интегральной суммы.
Общее обозначение определённого интеграла по фигуре E: ∫ f ( M )dE .
Итак, по определению |
|
|
E |
|
|
|
|
∫ f ( M )dE = lim |
n |
|
|
∑ f ( Mi )∆Ei . |
(10.6) |
||
E |
d →0 i=1 |
|
|
Замечание. В разделе 7 была рассмотрена фигура – отрезок [a, b], по которой аналогичным образом ввели понятие определённого интеграла от функции на отрезке (т. е. был рассмотрен частный случай).
Для отдельных рассматриваемых фигур определения, обозначения и названия интегралов следующие:
1) фигура – плоская область D:
двойной интеграл ∫∫ f ( M )dS = lim |
n |
||
∑ f ( Mi )∆Si ; |
|||
2) фигура – линия L: |
D |
d →0 i=1 |
|
|
n |
|
|
криволинейный интеграл ∫ |
|
|
|
f ( M )dL = lim ∑ f ( Mi )∆Li ; |
|||
L |
|
d →0 i=1 |
|
3) фигура – тело T:
тройной интеграл ∫∫∫
T
4) фигура – поверхность Σ:
поверхностный интеграл
n
f ( M )dV = lim ∑ f ( Mi )∆Vi ;
d →0 i=1
∫∫ f ( M )dσ = lim |
n |
|
∑ f ( Mi )∆σi . |
||
Σ |
d →0 i=1 |
|
Так же, как и для определённого интеграла на отрезке, f(M)dE называют подынтегральным выражением, эта запись напоминает об устройстве интегральных
сумм, состоящих из слагаемых f(Mi)∆Ei.
Иногда бывает удобно условно понимать интеграл ∫ f ( M )dE как «сумму
E
бесконечно большого числа бесконечно малых слагаемых вида f(M)dE». При таком неточном, упрощённом подходе величину f(M)dE надо понимать как произве-
124
дение меры dE бесконечно малого элемента фигуры на значение функции f(M) в произвольной точке M этого элемента.
Сформулируем достаточное условие существования определённого интеграла по фигуре:
если функция f(M) непрерывна на замкнутой, т. е. включающей границу, и ограниченной фигуре, то интеграл от неё существует.
В дальнейшем будем предполагать, что функция f и фигура E таковы, что достаточное условие существования интеграла выполнено.
Решение задачи о массе фигуры E было получено в виде
n
m( E ) = lim ∑ f ( Mi )∆Ei , где ρ(M) = f(M) – функция плотности. Отсюда сле-
d →0 i=1
дует механический смысл определённого интеграла по фигуре Е: |
|
∫ρdE = m( E ) , |
(10.6′) |
E
т. е. определённый интеграл по фигуре от плотности равен массе этой фигуры.
1.4. Свойства определённого интеграла по фигуре.
В главе 7 были рассмотрены свойства определённого интеграла на отрезке [a, b] (по фигуре [a, b]). Так как определённые интегралы по другим четырём типам фигур имеют подобное устройство, то ранее рассмотренные свойства будут справедливы для всех других типов интегралов. Сформулируем основные из них.
Свойство 1 (о мере фигуры).
Если функция f(M) тождественно равна единице на фигуре E, то интеграл от неё дает меру S(E) этой фигуры:
∫1 dE = S( E ) .
E
Этот результат полезно записать подробно для всех типов интегралов:
∫∫dS = S( D ) – площадь фигуры D; |
(10.7) |
D |
|
∫dL = l( L ) – длина линии L; |
(10.8) |
L |
|
∫∫∫dV =V (T ) – объём тела T; |
(10.9) |
T |
|
∫∫dσ = S( Σ ) – площадь поверхности Σ. |
(10.10) |
Σ |
|
Эти результаты непосредственно следуют из определения интеграла по фигуре, если положить f(M) ≡ 1.
125

Свойство 2 (линейность интеграла).
α |
f |
1 |
( M ) +α |
2 |
f |
2 |
( M ) dE = α |
1 |
∫ |
f |
1 |
( M )dE +α |
2 |
∫ |
f |
2 |
( M )dE , |
(10.11) |
||
∫ 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
E |
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
E |
|
|
|
|
где α1 , α2 |
– произвольные числа, |
f1(M), |
f2(M) – функции заданные на фигуре E. |
|||||||||||||||||
Свойство 3 (аддитивность интеграла). |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
∫ f ( M )dE = ∫ |
f ( M )dE + ∫ f ( M )dE , |
(10.12) |
|||||||||||
|
|
|
|
|
|
|
E |
E1 |
|
|
|
E2 |
|
|
|
|
|
|
||
где E = E1 E2 – объединение фигур E1 и E2, причём пересечение |
E1 ∩ E2 – |
|||||||||||||||||||
или пустое множество, или состоит из граничных точек. |
|
|
|
|
||||||||||||||||
Свойство 4 (об оценке интеграла). |
|
|
|
A ≤ f(M) ≤ B, |
|
|||||||||||||||
Пусть для любой точки Μ фигуры Ε справедливо |
|
тогда |
||||||||||||||||||
|
|
|
|
|
|
|
|
A S( E ) ≤ ∫ f ( M )dE ≤ B S( E ) , |
(10.13) |
|||||||||||
где S(E) – мера фигуры E. |
|
E |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Свойство 5 (о среднем значении функции). |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
∫ f ( M )dE = |
f ( c ) S( E ) , |
|
|
|
(10.14) |
|||||||
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
где точка с – некоторая точка фигуры E, f(с) называется средним значением функ-
ции f на фигуре E.
Перейдём к вычислению определённых интегралов по каждой из четырёх фигур. Непосредственное вычисление интегралов, как пределов интегральных сумм, чрезвычайно громоздко и применяется очень редко. Познакомимся с другими методами вычисления.
2. Вычисление криволинейного интеграла
Вычисление криволинейного интеграла ∫ f ( M )dL сводится к вычислению
L
обычного определённого интеграла.
Рассмотрим некоторые случаи (в зависимости от способа задания линии). 1) Пусть линия L на плоскости Oxy задана уравнением y = ϕ(x), x [a, b].
В этом случае дифференциал dL дуги линии L вычисляется по формуле dL = 1 + (ϕ′( x ))2 dx , а f ( M ) = f ( x,ϕ( x )), поэтому подынтегральное вы-
ражение f ( M )dL = f ( x,ϕ( x )) 1 + (ϕ′( x ))2 dx, при этом x [a, b]. Интегри-
руя этот результат в пределах возможного изменения переменной x, получим
126
