Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

zaicevVM_2

.pdf

Скачиваний:

Добавлен:

14.02.2015

Размер:

1.33 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 163 4 5 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

1) ∫

dx = A∫

d( x − c ) = A ln

x − c

+ C .

x − c

( x − c )−k +1

2) ∫

dx =

A∫( x − c )−k d( x − c ) = A

+ C , k ≠ 1 .

( x

−k + 1

− c )

3) Интегрирование дроби

+ N

рассмотрим только для случая t =

( x + px+q )

1. Вначале выделим полный квадрат в знаменателе:

+ px + q

= x

+ 2x

+ q −

= x +

+ a

Мыобозначилиq −

= a2 длякраткости, учитывая, что дискриминант

− q < 0

(по определению простейшей дроби), а значит q −

> 0 .

Вычисляем интеграл с помощью замены переменной:

∫

Mx + N

dx =∫

Mx + N

dx =

+ px + q

x +

+ a

tdt

M ∫

+ N

−

∫

+ a

x +	p	= t			Mt −	Mp	+ N

				∫		2		dt =
	2		=
					t 2	+ a2
dx = dt

Первый интеграл вычисляется подведением под знак дифференциала:

∫			tdt		dx =	1	∫	d( t 2		+ a2 )		=	1	ln( t	2	+ a	2	) + C .
	t	2	+ a	2		2		t	2	+ a	2		2

Интеграл во втором слагаемом является табличным:

∫

dx =

arctg

+ C .

+ a

Итак, возвращаясь к переменной x, получим:

∫

Mx + N

ln( x

+ px + q) +

N − 0,5Mp

x + 0,5 p

dx =

arctg

+ C .

x2 + px + q

q − 0,25 p2

Пример 7.10. Найти J = ∫	x4	− x2 + 5 x − 2				dx .
	x	3	− 2 x	2	+ 2 x

Решение. Подынтегральная дробь является неправильной. Выделим целую часть, поделив числитель на знаменатель. Получим

x4 − x2 + 5 x − 2		= x + 2	+	x2 + x − 2		.
x3 − 2 x2	+ 2 x			x3 − 2 x2	+ 2 x

Разложим получившуюся правильную дробь на сумму простейших:

x2 + x − 2

Bx + D

x3 − 2 x2 + 2 x

x (x2 − 2 x + 2)

x2 − 2 x + 2

Избавимся в рассматриваемом разложении от знаменателей, умножая обе час-

ти равенства на x(x2 – 2x + 2):

x2 + x − 2 = A(x2 − 2 x + 2)+(Bx + D) x .

Найдём коэффициенты А, В, D, приравнивая коэффициенты при одинаковых

степенях х в полученном тождестве:

1 = A + B,

1 = −2 A + D,

−2

= 2A.

Решение этой системы: A = –1, B = 2, D = –1.

Следовательно:

2x −1

J =

x +

−

dx =

xdx + 2

dx −

dx .

∫

∫ x2 − 2 x + 2

2 − 2 x + 2

Имеем:

∫

xdx =

+C1 ;

∫

dx = 2 x +C

2 ;

∫

= ln | x | +C3

;

∫

2x −1

= ∫

2x −1

dx =

x −1

= t x = t

+ 1, dx = dt

− 2x + 2

( x −

1 )

d (t2 +1)

=∫

2( t +1)−1

dt =

∫

2tdt

+∫

= ∫

+arctgt =ln(t

2 +1)+arctg t +C4 =

t2 +1

= ln((x −1)2 + 1)+ arctg (x −1)+C4 .

Итак,

J =

+2x −ln

+ln(x2 −2x + 2)+arctg(x −1)+C .

6. Понятие определённого интеграла

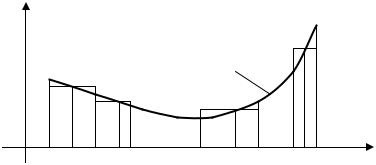
Пусть на отрезке [a,b]				задана функция		f (x) . Выполним следующие дейст-
вия (см. рисунок 1):				x0 = a, x1 , x2 , ... , xn = b (x0 < x1 < ...< xn ) разде-
1) с помощью точек				x0 = a, x1 , x2 , ... , xn = b (x0 < x1 < ...< xn ) разде-
лим отрезок [a,b]на n частичных отрезков [x0 , x1 ],[x1 , x2 ], ... ,[xn−1 , xn ];
y
							B
							f(cn )
	A	f(c1)			y = f(x)
			f(c2)			f(ck)
0	a						b
	x0	c1	x1 c2 x2		. . . xk–1	ck	xk . . . xn–1cnxn	x
					Рисунок 1
2) выберем на каждом отрезке [ xi−1 , xi ],							i = 1, ... , n по одной произволь-
ной точке ci [xi−1 , xi ] и вычислим значение функции в ней, т. е.								f (ci ) ;
3) для	каждого		отрезка		[ xi−1 , xi ],	i = 1, ... , n составим		произведение

f(ci )∆xi , где ∆xi = xi − xi−1 – длина этого отрезка;

4)составим сумму всех таких произведений

Sn = f (c1 )∆x1 + f (c2 )∆x2 + ...+ f (cn )∆xn = ∑ f (ci )∆xi , (7.3)

i=1

называемую интегральной суммой функции f (x) на отрезке [a,b].

Если существует конечный предел последовательности интегральных сумм

при n → ∞ (при условии, что λ = max ∆xi →0 ), который не зависит ни от спо-

соба разбиения отрезка [a,b] на частичные отрезки, ни от выбора точек в них, то этот предел называется определённым интегралом от функции f (x) на отрезке

[a,b] и обозначается ∫ f ( x )dx . Таким образом,

b		n
∫ f ( x )dx = lim		∑ f (ci )∆xi .	(7.4)
	n→∞
a	(λ→0) i=1

Числа a и b называются соответственно нижним и верхним пределами интегрирования.

Замечание. Понятие определённого интеграла распространяют на случаи, когда a > b и a = b :

b	a
при a > b полагают ∫ f (x)dx = −∫ f (x)dx ;
a	b

при a = b полагают ∫ f (x)dx = 0 .

Сформулируем теорему существования определённого интеграла:

если функция f (x) ограничена на отрезке [a,b] и непрерывна на нём всюду,

кроме, быть может, конечного числа точек (в которых функция может быть и

не определена), то определённый интеграл ∫ f ( x )dx существует.

При этом говорят, что функция f (x) интегрируема на отрезке [a,b].

Геометрический смысл определённого интеграла: если f (x) ≥ 0 на отрезке

[a,b], то ∫ f ( x )dx численно равен площади криволинейной трапеции aABb (см.

рисунок 1).

Механический смысл определённого интеграла: путь S, пройденный точкой за промежуток времени от t = a до t = b , равен определённому интегралу от скоро-

сти v (t ) : S = ∫v (t )dt .

7. Основные свойства определённого интеграла

1) Свойство линейности определённого интеграла:

если A, B – произвольные числа, то

b		b	b
∫( Af1	(x) + Bf2	(x))dx = A∫ f1	(x)dx + B∫ f2	(x)dx ,
a		a	a

т. е. интеграл от суммы равен сумме интегралов, а постоянный множитель можно

выносить за знак определённого интеграла.

2) Свойство аддитивности определённого интеграла:

b	c	b
∫ f ( x )dx = ∫ f ( x )dx + ∫ f ( x )dx, c (a,b) ,
a	a	c

т. е. интеграл по всему отрезку равен сумме интегралов по его частям. 3) Свойство монотонности определённого интеграла:

если x [a, b] f(x) ≤ g(x), то ∫b	f ( x )dx ≤ ∫b g( x )dx ,
a	a

т. е. при a < b можно интегрировать неравенство почленно.

4) «Теорема о среднем»:
если функция f (x)		непрерывна на отрезке [a,b], то
		c [a,b]:		b
		c [a,b]:		∫ f ( x )dx = f ( c )( b −a ) .
				a
		1	b
Число f (c) =		1	∫ f (x)dx	называется средним значением функции		f (x)
Число f (c) =	b	−a	∫ f (x)dx	называется средним значением функции		f (x)
	b	−a	a
на отрезке [a,b].			a
на отрезке [a,b].
8. Формула Ньютона-Лейбница
Если функция		F (x) является первообразной для непрерывной функции
					b
f (x) на отрезке [a,b], то определённый интеграл ∫ f ( x )dx можно вычислить
по формуле Ньютона-Лейбница:					a
по формуле Ньютона-Лейбница:
			b		b
			∫ f ( x )dx = F( x )		= F (b)− F (a) .	(7.5)
			∫ f ( x )dx = F( x )		= F (b)− F (a) .	(7.5)
			a		a

Запись F( x )

является краткой символической записью разности F (b)− F (a).

Пример 7.11. Вычислить определённые интегралы:

4		1			2	1 − x,			0 ≤ x < 1

1) ∫	2 x −		+ 3	dx ;	2) ∫ f (x)dx , если	f (x) = 1		, 1	< x ≤ 2	.
		x
1					0
							2
						x

Решение. 1) Подынтегральная функция непрерывна на отрезке [1,4], поэтому можно использовать формулу Ньютона-Лейбница:

4		1			4	4		1	4		4
							−			= (x	2 − 2 x + 3x)

∫	2 x −		+ 3	dx = 2	∫xdx − ∫x			2 dx + 3∫dx				=
		x
1					1	1			1			1

				= (	42 − 2	4	+ 3 4)−(12 − 2				1 + 3 1) = 22.

2)	Функция	f (x) ограничена и непрерывна во всех точках отрезка										[0,2],
кроме точки x = 1, где она имеет разрыв 1-го рода, значит она интегрируема.
Используя свойство аддитивности определённого интеграла, получим
2	1	2	1	2	1		x	2	1		1		2

∫ f ( x )dx = ∫		f ( x )dx + ∫ f ( x )dx =	∫(1 − x)dx + ∫			dx = x −				−				= 1.
					2		2				x		1
0	0	1	0	1	x				0

Все методы, позволяющие вычислять неопределённые интегралы, применимы и для вычисления определённых интегралов. В частности, можно использовать интегрирование по частям или производить замену переменной. При применении этих методов к определённым интегралам имеются некоторые особенности. Рассмотрим их.

Формула интегрирования по частям для определённого интеграла может быть записана в виде

∫udv = (uv )

− ∫vdu .

(7.6)

Пример 7.12. Вычислить ∫x sin xdx .

Решение.

= x,

dv =sinxdx

=(−xcos x)

π =π .

∫xsinxdx =

+∫cos xdx =−π cosπ +sinx

du =dx,

v =−cos x

Пусть для вычисления определённого интеграла ∫ f ( x )dx от непрерывной

функции сделана подстановка x =ϕ (t ) . Тогда, если:

1) функция

x =ϕ (t ) и её производная

x′ =ϕ′(t ) непрерывны на

отрезке

[α,β ];

2)множеством значений функции x =ϕ (t ) приt [α,β ]является отрезок [a,b];

3)ϕ (α) = a и ϕ (β ) = b ,

то справедлива формула замены переменной в определённом интеграле

∫b	β
∫b	f ( x )dx = ∫ f (ϕ( t ))ϕ′( t )dt .	(7.7)
a	α

Замечания.

1) Новые пределы интегрирования α и β являются корнями уравнений

ϕ(t ) = a и ϕ (t ) = b соответственно.

2)Иногда замена переменной в определённом интеграле производится не по формуле x =ϕ (t ) , а по формуле t = g (x) . Тогда новые пределы α и β легко оп-

ределяются: α = g (a) , β = g (b) . В этом случае должна существовать обратная функция x = g−1 (t ) .

3)При вычислении определённого интеграла по формуле (7.7) не нужно возвращаться к старой переменной интегрирования (как обязательно нужно делать в неопределённом интеграле), так как пределы интегрирования уже будут изменены

всоответствии с подстановкой.

4)При использовании подстановки в определённом интеграле необходимо проверять выполнение всех сформулированных условий, иначе может быть получен неверный результат.

Пример 7.13. Вычислить ∫4

с помощью подстановки tgx = t .

1 + 2 sin

Решение.

t 2

∫4

tgx = t ,

x = arctgt ,

dx =

sin

x =

1 + t 2

1 + 2 sin

x = 0

t = 0, x =

t = 1


1			dt			1		dt			1	1		dt					1	1		t	1	π
1			1 + t	2		1		dt			1	1		dt					1	1		t	1	π
= ∫			1 + t				= ∫			=		∫						=			arctg		=		.
= ∫				t	2		= ∫	1 + 3t	2	=	3	∫			2			=	3	1	arctg	1	=	3 3	.
0	1	+ 2					0					0	1			+ t	2			1		1	0
0							0					0	1				2
				+ t		2														3		3
						2							3
		1											3

9. Несобственные интегралы

Вводя определённый интеграл как предел интегральных сумм, мы предполагали, что отрезок интегрирования конечный, а подынтегральная функция ограничена на этом отрезке. Если хотя бы одно из этих условий не выполнено, данное выше определение теряет смысл. Рассмотрим некоторые возможные обобщения понятия определённого интеграла.

9.1. Несобственные интегралы с бесконечными пределами.

Пусть функция f (x) определена на промежутке [a,+∞) . Если существует

конечный предел	blim→+∞ ∫ f ( x )dx, то его называют несобственным интегралом
	a
от функции f (x)	на неограниченном промежутке [a,+∞)		(несобственный ин-
		+∞
теграл 1-го рода) и обозначают символом		∫ f ( x )dx. Таким образом, по опре-
делению		a
делению
	+∞	b
	∫ f ( x )dx = blim→+∞ ∫ f ( x )dx,		(7.8)
	a	a

если этот предел существует и конечен. В этом случае принято говорить, что несобственный интеграл существует или сходится. Если же этот предел не сущест-

вует или он бесконечен, то символу +∞∫ f ( x )dx никакого числового значения не

приписывают и, называя его по-прежнему несобственным интегралом, говорят, что этот несобственный интеграл не существует или расходится.

Аналогично определяется несобственный интеграл на промежутке (−∞,b]:

∫b	f ( x )dx = alim→−∞ ∫b	f ( x )dx	(7.8′)
−∞	a

и несобственный интеграл на всей числовой оси (−∞,+∞): 29

+∞	c	+∞
∫	f ( x )dx = ∫	f ( x )dx + ∫ f ( x )dx ,	(7.8″)
−∞	−∞	c

где с – любое число (при условии существования обоих несобственных интегралов справа).

Несобственные интегралы 1-го рода обладают рядом свойств, присущих определённым интегралам. В частности, для них можно записать обобщённые форму-

лы Ньютона-Лейбница:

+∞			+∞
+∞
∫
∫	f ( x )dx = F( x )		a = F( +∞ ) − F( a ),
a
a
∫b			−∞b = F( b ) − F( −∞ ) ,
∫b	f ( x )dx = F( x )		−∞b = F( b ) − F( −∞ ) ,
−∞
−∞
+∞∫	f ( x )dx = F ( x )	−∞+∞ = F ( +∞ ) − F ( −∞ ) .
+∞∫	f ( x )dx = F ( x )	−∞+∞ = F ( +∞ ) − F ( −∞ ) .
−∞
−∞

Здесь сделаны обозначения: lim F (x) = F (+∞),	lim F (x) = F (−∞) .
x→+∞	x→−∞

Пример 7.14. Исследовать на сходимость несобственный интеграл 1-го рода

+∞∫ dx , где р − произвольное число.

1 x p

+∞

x− p+1

, p > 1

+∞

Решение. а) Если р ≠ 1, то ∫

= p − 1

− p + 1

, p < 1 .

∞

б) Если р = 1, то

+∞

= ∞ .

∫ dx = ln x

+∞

Таким образом, несобственный интеграл ∫

сходится при р > 1 и расходится

+∞

при р ≤ 1. Например, ∫

сходится и равен 1 , а ∫

расходится.

9.2. Несобственные интегралы от неограниченных функций.

Пусть теперь функция f (x) определена на промежутке [a,b), интегрируе-

ма на любом отрезке [a,b1 ] , гдеb1 [a,b) и не ограничена в окрестности точки b. 30

<<< < Предыдущая 1 23 / 163 4 5 6 7 8 9 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.08.201988.04 Кб1Zadacha_1_5-7.docx
#
14.02.2015193.02 Кб31ZADAChI_1.doc
#
14.02.2015134.14 Кб66ZADAChI_V.doc
#
14.02.2015866.93 Кб199zadat-fkh.pdf
#
14.02.201515.12 Mб32zaginajlov-kvl.pdf
#
14.02.20151.33 Mб24zaicevVM_2.pdf
#
14.02.20151.25 Mб29zajcevVM.pdf
#
12.03.2016345.72 Кб28zarnitsina-e-g-mapp-549003aae0d37.pdf
#
14.02.20154.64 Mб56zarn_met_kp.pdf
#
14.02.2015527.89 Кб23zarn_met_lab.pdf
#
14.02.20152.32 Mб8Zaschita_ot_shuma_404.doc