Решение

Составим задачу, двойственную к исходной, и запишем ограничения:

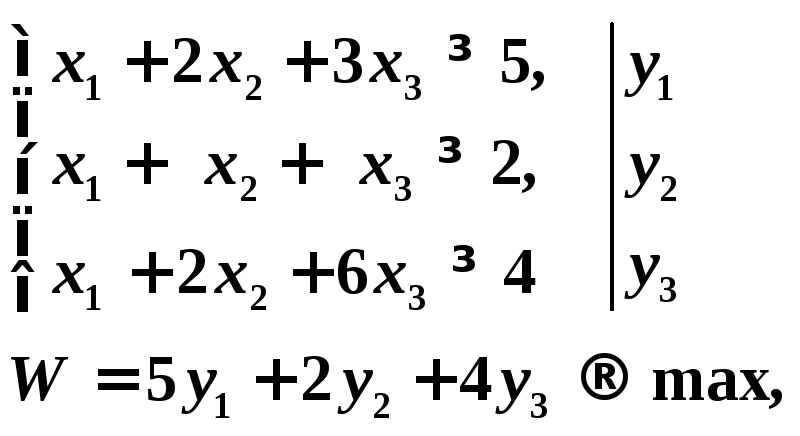
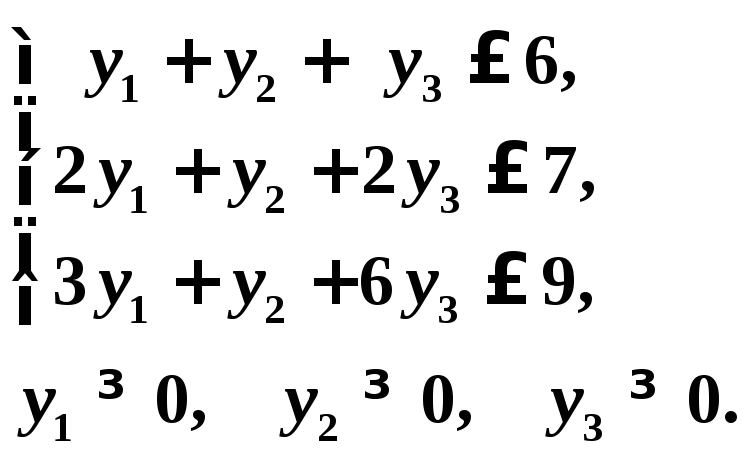
Решим полученную задачу симплекс – методом.

Сведем задачу на максимум к задаче на минимум. Для этого целевую функцию умножим на -1, получим

Вводим неотрицательные дополнительные переменные для приведения задачи к каноническому виду:

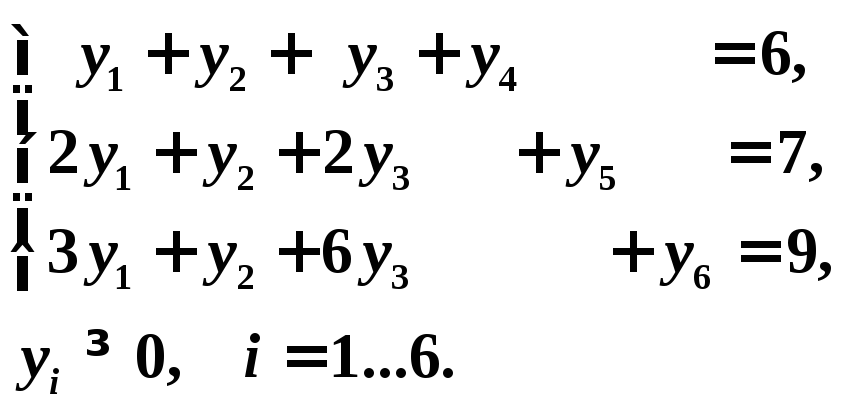
Базисные перемененные , свободные.

Выражаем базисные переменные через свободные:

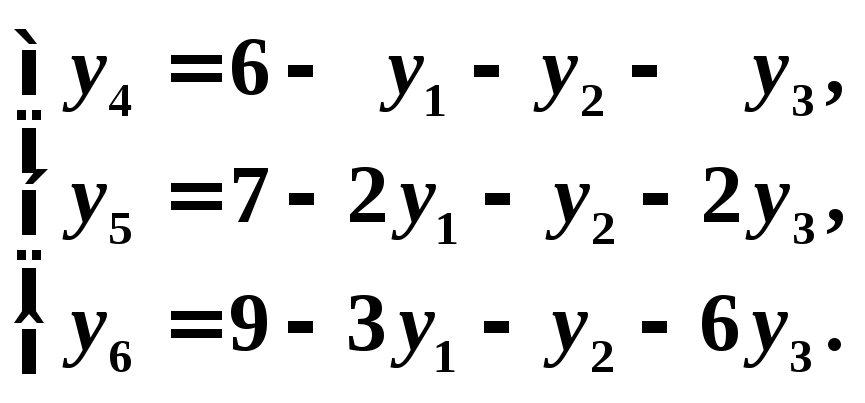
Получим систему уравнений допустимого вида.

Для составления первой симплекс – таблицы запишем задачу в виде:

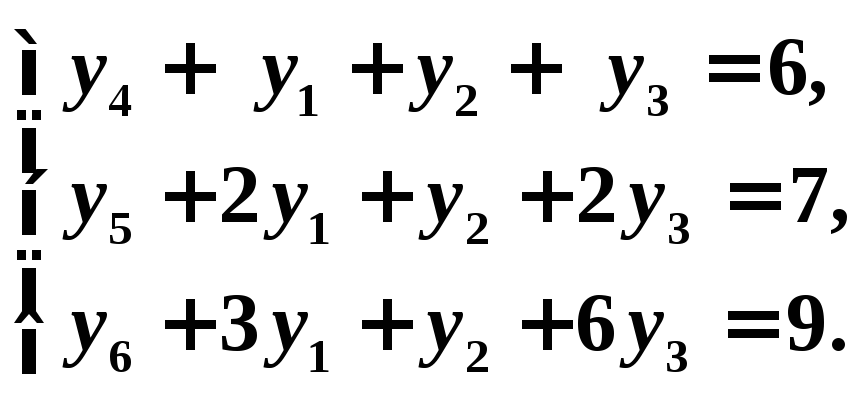
Таблица 1

Базисные переменные	Свободные члены							Отно- шение
	6	1	1	1	1	0	0
	7	2	1	2	0	1	0
	9	3	1	6	0	0	1
W	0	5	2	4	0	0	0

В последней строке есть положительные коэффициенты. Возьмем коэффициент в столбце переменной . Разрешающим элементом является3.

Строим таблицу 2.

Для этого умножаем выделенную стрелкой строку на 1/3и записываем результат вместо этой строки в таблицу 2.

Умножаем третью строку новой таблицы на (-1)и складываем с первой, умножаем на (-2)и складываем со второй, умножаем на (-5)и складываем с четвертой строкой старой таблицы.

Таблица 2

Базисные переменные	Свободные члены							Отно- шение
	3	0	2/3	-1	1	0	-1/3
	1	0	1/3	-2	0	1	-2/3
	3	1	1/3	2	0	0	1/3
W	-15	0	1/3	-6	0	0	-5/3

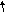
В новой таблице последняя строка имеет положительный коэффициент в столбце переменной . Разрешающим элементом является1/3.

Строим таблицу 3. Для этого умножаем выделенную стрелкой строку на и записываем результат вместо этой строки в таблицу 3.

Умножаем вторую строку новой таблицы на и складываем с первой, наи складываем с третьей и наи складываем с четвертой строкой предыдущей таблицы.

Таблица 3

Базисные переменные	Свободные члены
	1	0	0	3	1	-2	1
	3	0	1	-6	0	3	-2
	2	1	0	4	0	-1	1
W1	-16	0	0	-4	0	-1	-1

В полученной таблице последняя строка не имеет положительных чисел в последних шести столбцах. Значит, достигнуто оптимальное решение. Базисным решением для переменных являются соответственно свободные члены. Базисное решение для свободных переменныхравно нулю. Таким образом, оптимальное решение имеет вид:

=2, =3,=1,=0,=0,=0,

,

.

Подставим оптимальное решение в систему ограничений. Получим, что первое второе ограничение выполняется как строгое неравенство:

По теореме 2 следует, что соответствующая координата оптимального решения двойственной задачи, то есть исходной задачи, равна нулю: .

Учитывая это и в силу теоремы 2, из системы ограничений исходной задачи получим систему:

Данная система получаетcя в силу того, что, следовательно первое и второе ограничения исходной задачи удовлетворяются оптимальным решением как равенство.

Решив систему:

получим .

Оптимальное решение исходной задачи

Ответ:

3. Экономико-математическая модель межотраслевого баланса (модель Леонтьева).

Рассмотрим модель межотраслевого баланса, называемую еще моделью Леонтьева или моделью «затраты-выпуск».

Предположим, что производственный сектор народного хозяйства разбит на nотраслей (энергетика, машиностроение, сельское хозяйство и т.д.).

Рассмотрим отрасль i, i = 1, 2,…,n. Она выпускает некую продукцию за данный промежуток времени (например, за год) в объеме x_i, который еще называют валовым выпуском. Часть объема продукции x_i, произведенная i-ой отраслью используется для собственного производства в объеме x_ii, часть – поступает в остальные отрасли j = 1, 2,…,nдля потребления при производстве в объемах x_ij, и некоторая часть объемомy_i– для потребления в непроизводственной сфере, так называемый объем конечного потребления. Перечисленные сферы распределения валового продукта i-ой отрасли приводят к соотношению баланса

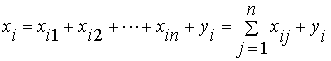,i= 1, 2,…,n.

Введем коэффициенты прямых затратa_ij, которые показывают, сколько единиц продукции i-ой отрасли затрачивается на производство одной единицы продукции в отрасли j. Тогда можно записать, что количество продукции, произведенной в отрасли i в объеме x_ijи поступающей для производственных нужд в отрасль j, равно

Считаем сложившуюся технологию производства во всех отраслях неизменной (за рассматриваемый период времени), означающую, что коэффициенты прямых затрат a_ijпостоянны. Тогда получаем следующее соотношение баланса, называемого моделью Леонтьева

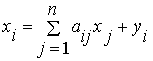,i= 1, 2,…,n. (1)

Введя вектор валового выпуска X, матрицу прямых затрат A и вектор конечного потребления Y

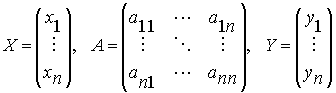
модель Леонтьева (1) можно записать в матричном виде

X=AX+Y(2)

Матрица A ≥ 0, у которой все элементы a_ij≥ 0 (неотрицательны), называется продуктивной матрицей, если существует такой неотрицательный вектор X ≥ 0, для которого выполняется неравенство

X>AX.

Это неравенство означает, что существует хотя бы один режим работы отраслей данной экономической системы, при котором продукции выпускается больше, чем затрачивается на ее производство. Другими словами, при этом режиме создается конечный (прибавочный) продукт Y = X – AX> 0.

Модель Леонтьева с продуктивной матрицей Aназывается продуктивной моделью.

Существует несколько критериев продуктивности матрицы A. Один из них говорит о том, что матрица A продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы.

Для проверки продуктивности матрицы A также достаточно существования обратной матрицы B = (E–A)^-1с неотрицательными элементами, где матрица E – единичная матрица

.

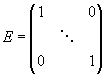С помощью модели Леонтьева (2) можно выполнить три вида плановых расчетов, при условии соблюдения условия продуктивности матрицы A:

1) Зная (или задавая) объемы валовой продукции всех отраслей X можно определить объемы конечной продукции всех отраслей Y

Y= (E–A)X

2) Задавая величины конечной продукции всех отраслей Yможно определить величины валовой продукции каждой отрасли

X= (E–A)^-1Y(3)

3) Задавая для ряда отраслей величины валовой продукции, а для всех остальных отраслей – объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых.

Матрица

B = (E–A)^-1

называется матрицей полных материальных затрат. Ее смысл следует из матричного равенства (3), которое можно записать в виде X=BY. Элементы матрицы B показывают, сколько всего необходимо произвести продукции в i-ой отрасли, для выпуска в сферу конечного потребления единицы продукции отрасли j.

3. Различная постановка задачи межотраслевого баланса

Пример 1.

Объемы промежуточной продукции в линейной статической модели Леонтьева представлены матрицей , а объемы валовых выпусков – вектором . Найти объемы конечного продукта.

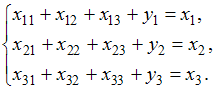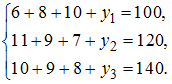Решение:В модели Леонтьева валовой выпуск , конечный продукт и промежуточное потребление связаны системой уравнений:ТогдаТо есть .

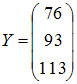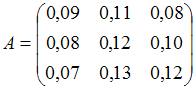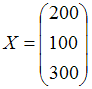Пример 2. Матрица коэффициентов прямых затрат линейной статической модели Леонтьева имеет вид , а объемы валовых выпусков представлены вектором . Найти объемы промежуточной продукции.

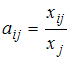Решение:Коэффициенты прямых затрат вычисляются по формуле , где – объем промежуточной продукции -ой отрасли, который используется в -ой отрасли, – объем валового выпуска в -ой отрасли. Тогда , то есть .

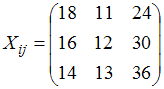В линейной статической модели Леонтьева объемы конечного продукта представлены вектором , объемы валовых выпусков – вектором . Тогда объемы промежуточной продукции  можно представить матрицей …

Решение: В модели Леонтьева валовой выпуск , конечный продукт и промежуточное потребление связаны системой уравнений: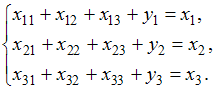Тогда объемы промежуточной продукции  можно представить матрицей:.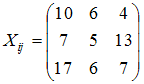

Пример 4.

Статическая линейная модель межотраслевого баланса Леонтьева представлена системой уравнений: 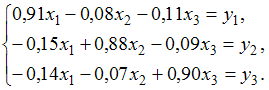Найти матрицу коэффициентов прямых затрат.

Решение: Статическая линейная модель межотраслевого баланса Леонтьева в матричной форме моделируется системой , где – единичная матрица. Тогда матрица коэффициентов прямых затрат будет равна: .

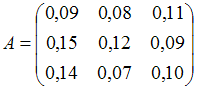Пример 5. Статическая линейная модель Леонтьева многоотраслевой экономики продуктивна. Укажите номер ячейки, где записана матрица коэффициентов прямых затрат:

a) ;	b) ;
c) ;	d)

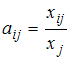Решение: Во-первых, коэффициенты прямых затрат вычисляются по формуле , где – объем промежуточной продукции -ой отрасли, который используется в -ой отрасли, – объем валового выпуска в -ой отрасли, то есть . Во-вторых, модель Леонтьева продуктивна, если сумма элементов каждой строки матрицы не больше единицы и хотя бы для одной строки эта сумма меньше единицы. Обоим этим условиям удовлетворяет матрица

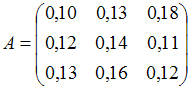
Пример 6.

Укажите номер ячейки, где записана матрица коэффициентов прямых затрат статической линейной модели Леонтьева:

a) ;	b) ;
c) ;	d)

Решение: Коэффициенты полных затрат показывают, на сколько единиц увеличится валовой выпуск ой отрасли при увеличении конечного выпуска в ой отрасли на одну единицу. Поэтому , а , при . Этим условиям удовлетворяет матрица .

Пример 7. Матрица коэффициентов прямых затрат линейной статической модели Леонтьева имеет вид 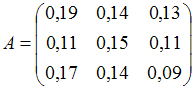. Запишите систему уравнений модели межотраслевого баланса

Решение:

Статическая линейная модель межотраслевого баланса Леонтьева в матричной форме моделируется системой , где – единичная матрица. В данном случае , тогда система уравнений модели межотраслевого баланса выглядит следующим образом:

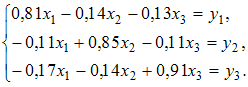
Пример 8. В линейной статической модели Леонтьева объемы конечного продукта представлены вектором , матрица коэффициентов полных затрат имеет вид . Найти объемы валовых выпусков.

Решение: Объемы валовых выпусков (вектор) определяются в модели межотраслевого баланса из уравнения , где – матрица коэффициентов полных затрат, а – вектор конечного продукта. Тогда

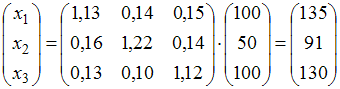
Пример 9.В таблице приведены данные об исполнении баланса за отчетный период в усл. ден. ед.:

№ п/п	Отрасль	Потребление			Конечный продукт	Валовой выпуск
		1	2	3
1	Добыча и переработка углеводородов	5	35	20	40	100
2	Энергетика	10	10	20	60	100
3	Машиностроение	20	10	10	10	50

Требуется найти объем валового выпуска каждого вида продукции, если конечное потребление по отраслям увеличить соответственно до 60, 70 и 30 условных денежных единиц.

Решение.

Выпишем векторы валового выпуска и конечного потребления и матрицу коэффициентов прямых затрат

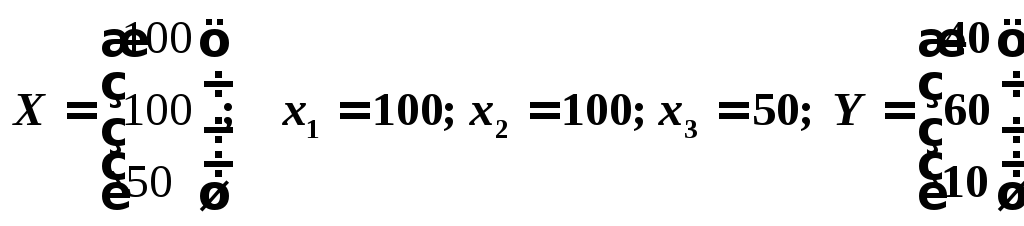
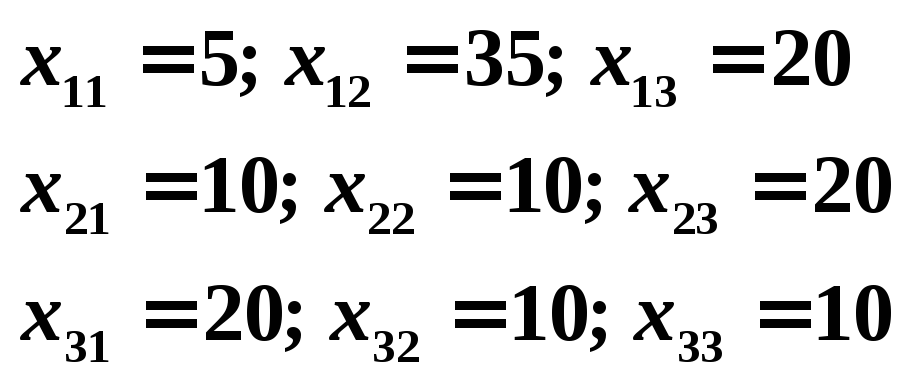
По формуле вычислим коэффициенты прямых затрат:

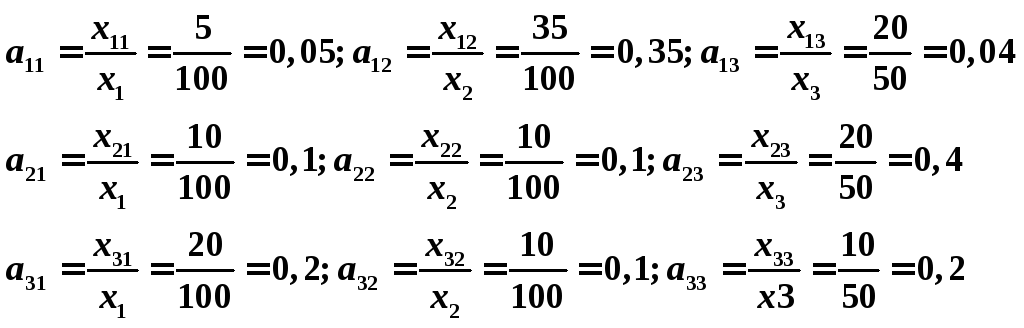
Запишем матрицу прямых затрат:

Она является неотрицательной и удовлетворяет критерию продуктивности:

max{0,05 + 0,1+02=0,35; 0,35 + 0,1+0,1=0,55 ; 0,04+0,4+0,2=0,64}=max{0,35; 0,55; 0,64} = 0,64 < 1.

Поэтому для любого вектора конечного продукта Y можно найти необходимый объем валового выпуска X по формуле X=(E–A)-1Y.

Определим матрицу полных затрат S=(E–A)-1:

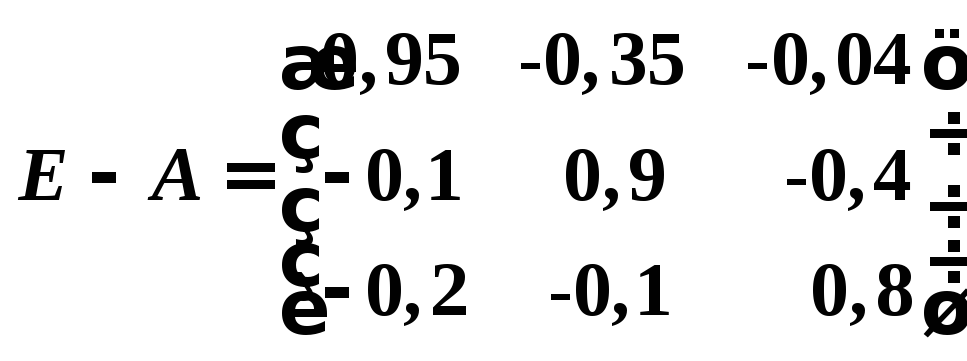
Так как |E−A|=0,5824, то

По условию новый вектор конечного продукта

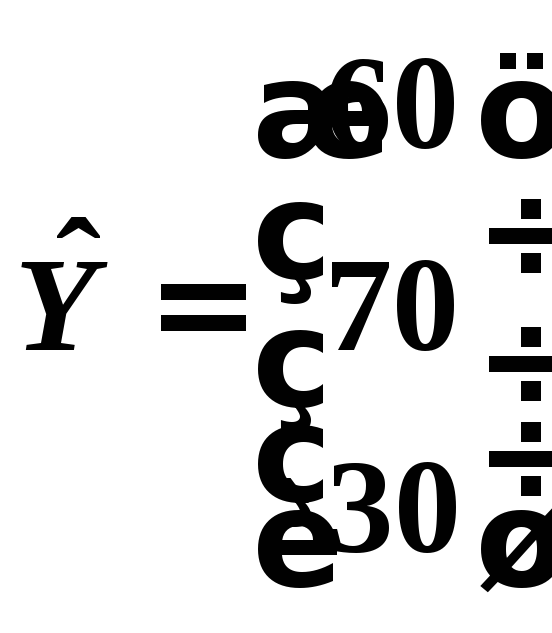
Тогда по формуле X=(E–A)-1Y получаем новый вектор валового выпуска:

Вычислим, на сколько процентов новые значения компонент вектора валового продукта больше, чем для исходного. Найдем приращения компонент:

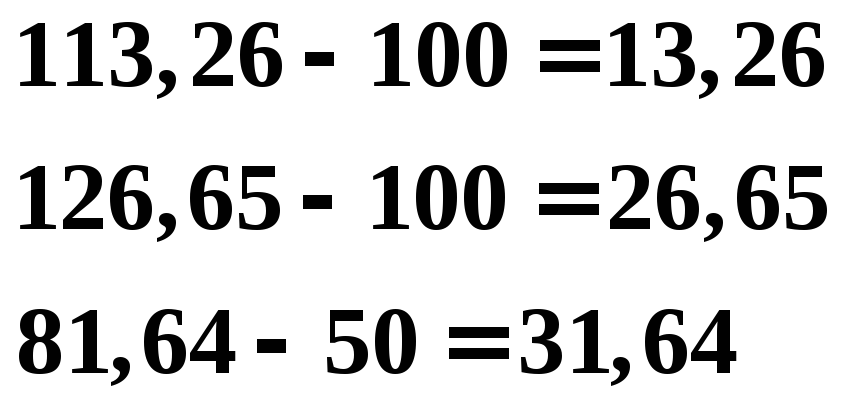
и выразим эти значения в процентах от исходных компонент:

Таким образом, для того чтобы обеспечить заданное увеличение компонент вектора конечного продукта Y, необходимо увеличить валовые выпуски (компоненты вектора X) в следующих пропорциях: добычу и переработку углеводородов на 13,26%, уровень энергетики — на 26,65% и выпуск продукции машиностроения — на 26,52% по сравнению с отчетным периодом.

3. Решение задачи межотраслевого баланса (модель Леонтьева)средствами Excel.

Задача. Экономическая система состоит из трех отраслей, для которых матрица прямых затрат A и вектор конечного продукта Y известны:

.

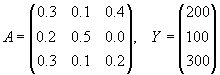Определить:

1) Матрицу коэффициентов полных материальных затрат B

2) Проверить продуктивность матрицы A

2) Вектор валового выпуска X

3) Межотраслевые поставки продукции x_ij

 

Математическая модель и последовательность расчетов

Модель Леонтьева имеет вид

X=AX+Y.

Матрица полных материальных затрат Bравна

B = (E–A)^-1

Продуктивность матрицы A проверяется, по вычисленной матрице B. Если эта матрица существует и все ее элементы неотрицательны, то матрица A продуктивна.

Вектор валового выпуска X рассчитывается по формуле

X=BY

Межотраслевые поставки продукции x_ijвычисляются по формуле

x_ij=a_ijx_j

 

Процесс решения задачи средствами Microsoft Excel

Для решения задачи межотраслевого баланса необходимо уметь выполнять с помощью Excel следующие операции над матрицами:

- Умножение матрицы на вектор

- Умножение двух матриц

- Транспонирование матрицы или вектора

- Сложение двух матриц

Задача. Задана матрица прямых затратA=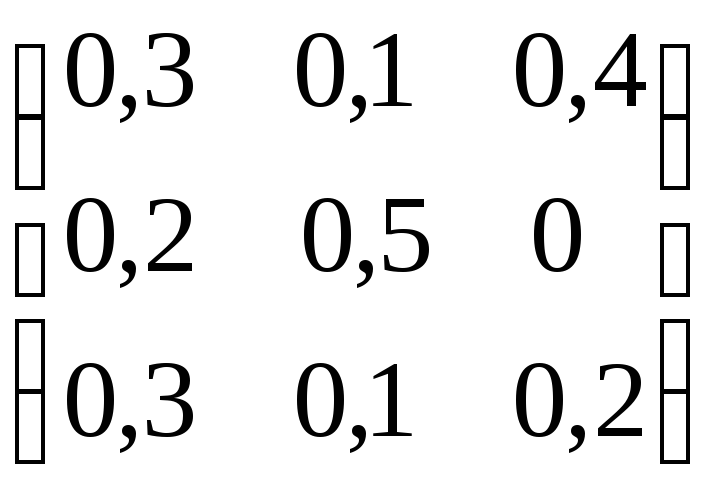и вектор конечного потребления. Найти вектор валового выпуска и матрицу межотраслевых постравок.
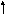
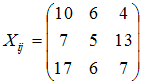
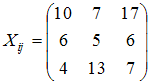
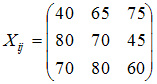
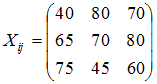
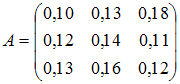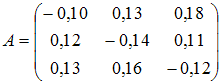