Государственное образовательное учреждение

высшего профессионального образования

«Алтайский государственный технический университет

им. И.И. Ползунова»

Л.П. Афонькина, EГ. Никифорова

Математические методы

в экономике

Учебно-методическое пособие

Барнаул – 2014

УДК 519.852 (075.8)

Л.П. Афонькина, Е.Г. Никифорова Математические методы в экономике: Учебно-методическое пособие. – Алт. гос. техн. ун-т им. И.И. Ползунова. – Барнаул: АлтГТУ, 2012. – 76 с.

Содержание пособия соответствует государственному образовательному стандарту высшего профессионального образования по экономическим специальностям. В пособии рассматриваются вопросы построения математических моделей производственных задач, графическое решение задач линейного программирования и симплекс-метод и модель межотраслевой экономики Леонтьева, .

В пособии приведено большое количество подробно разобранных примеров, варианты заданий для индивидуальной работы.

Пособие предназначено для студентов экономических специальностей.

Рекомендовано к изданию кафедрой высшей математики АлтГТУ

Рецензент – к.т.н., доцент Зайцев В.П.

Содержание Введение

Математические методы в экономике— научное направление в экономике, посвящённое исследованию экономических систем и процессов с помощью математических моделей. Математические методы являются важнейшим инструментом анализа экономических явлений и процессов, построения теоретических моделей, позволяющих отобразить существующие связи в экономической жизни, прогнозировать поведение экономических субъектов и экономическую динамику.

аппарат математического моделирования и оптимизации экономических процессов и систем дает возможность оптимизировать торговые стратегии на бирже, управлять проектами, минимизировать риски, прогнозировать спрос и предложение на рынке товаров и услуг, развивать и повышать эффективность производства.

Предлагаемое пособие посвящено лишь некоторым разделам математических методов в экономике. Здесь рассмотрены задача линейного программирования; построение математических моделей задач линейного программирования; графическое решение задач с двумя переменными, универсальный метод, называемый симплекс-методом; двойственные задачи а также математическая модель межотраслевого баланса Леонтьева

1. Построение математических моделей производственных задач

В настоящее время экономист должен иметь представление о математическом аппарате решения экономических задач, уметь математически грамотно сформулировать задачу, понимать технику расчетов. В данном разделе приводятся содержательные примеры, иллюстрирующие приемы математического моделирования конкретных экономических ситуаций. В реальной ситуации из полученной математической модели требуется получить конкретные практические рекомендации. Способы получения такой информации (решение задачи) с последующим экономико-математическим анализом полученных результатов рассматриваются в следующих разделах пособия.

1. ЗАДАЧА ПЛАНИРОВАНИЯ ПРОИЗВОДСТВА

Пример 1.Оптимизация плана производства(Сколько производить?)

Предприятие изготавливает два вида изделий, использую три вид сырья. Нормы расхода сырья на производство единицы продукции каждого вида, запасы сырья и прибыль от реализации одной единицы продукции указаны в следующей таблице:

Вид сырья	Нормы расхода сырья на единицу продукции		Запас сырья
	1-го вида x1	2-го вида x2
	3	5	120
	14	12	400
Прибыль от реализации единицы продукции	30	35

Решение.Пустьх₁ —объем выпуска продукта 1,х₂ — объем выпуска продукта 2. Тогда задача может быть опи­сана в виде следующей модели линейного программирования:

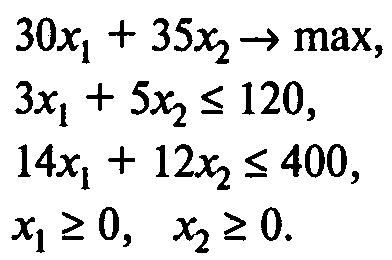
Пример2.Производить или покупать?

определения плана произ­водства для случая, когда закупка готовой продукции для последующей реализации может оказать­ся для производителя предпочтительнее, чем использование собственных мощностей

Предприятие по контракту должно изготовить два вида изделий в определенных количествах, используя два вида сырья. Нормы расхода сырья на производство единицы продукции каждого вида, запасы сырья и прибыль от реализации одной единицы продукции указаны в следующей таблице:

Вид сырья	Нормы расхода сырья на единицу продукции		Запас сырья
	1-го вида x1	2-го вида x2
	3	5	20
	14	12	42
Стоимость изготовления изделия	35	45
Стоимость покупки изделия	56 z1	66 z2
Обязательства поставок	100	120

Из-за ограничений на запасы сырья предприятие не может выполнить обязатель­ства по контракту. Выход заключается в следующем: фирма долж­на купить какое-то количество изделий у других производителей, чтобы использовать эти закупки для выполнения контракта. В таблица приводятся соответствующие затраты

Цель состоит в том, чтобы обеспечить выполнение кон­тракта с минимальными издержками. Другими словами, нужно принять решение: сколько изделий каждого вида производить у себя, а сколько — закупать со стороны для того, чтобы выполнить контракт с ми­нимальными издержками.

Решение.Введем обозначения:

x₁ — количество изделий 1, производимого предприятием;

z₁— количество изделий 1, закупаемого предприятием;

x₂ —количество изделий 2, производимого предприятием;

z₂— количество изделий 2, закупаемого предприятием.

Модель линейного программирования выглядит следующим образом:

- целевая функция

Ограничения на спрос:

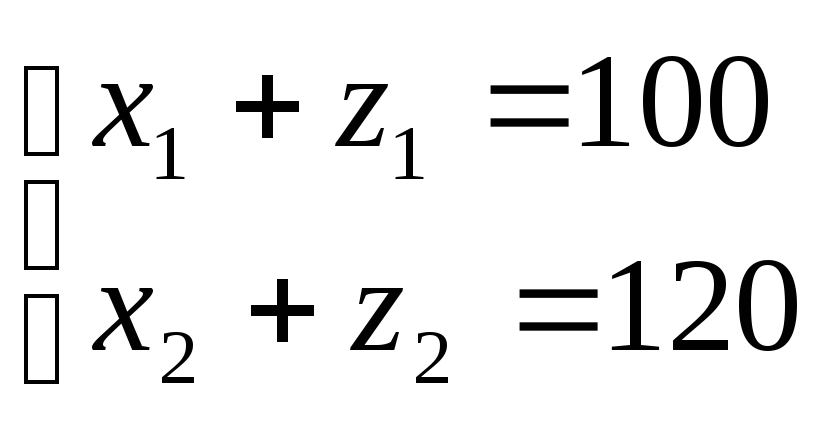
Ограничения по запасам сырья:

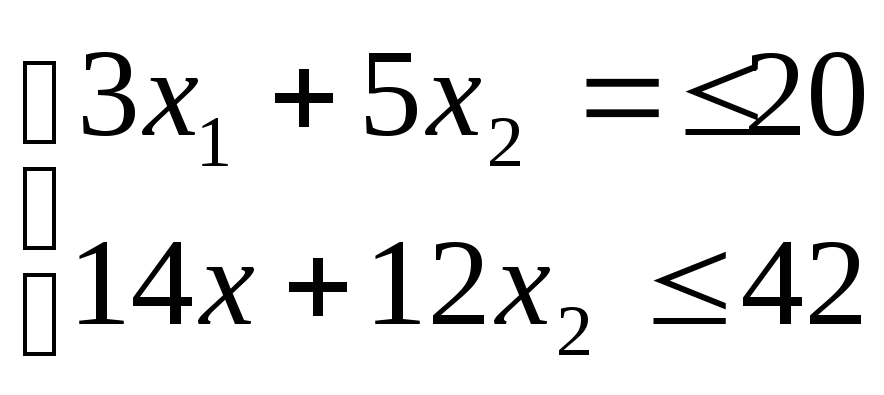
2. ЗАДАЧА О СМЕСЯХ

Введем обозначения:

п —количество исходных ингредиентов;

т —количество компонентов в смеси;

х_j —количествоj-го ингредиента, входящего в смесь;

а_ij —количествоi-го компонента вj-м ингредиенте;

с_j—стоимость единицыj-го ингредиента;

b_i— количествоi-го компонента в смеси.

МодельА:

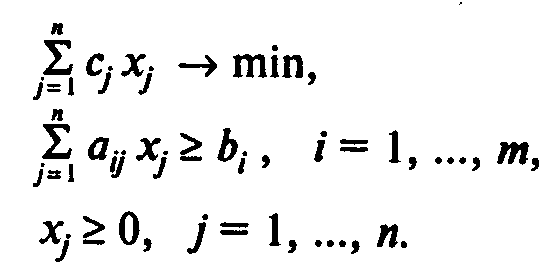
Здесь (1) — целевая функция (минимум затрат на получение смеси);

(2)— группа ограничений, определяющих содержание ком­понентов в смеси;

(3) — ограничения на неотрицательность переменных.

Пример 1. Производится кормление различными видами кормов, включающих известные ингредиенты (витамины, питательные вещества и т.п.). Пусть готовится два вида кормов, включающих витамины. Нормы потребления различных видов витаминов одним животным указаны в таблице:

Вид витамина	Необходимый минимум потребления витаминов	Нормы расхода витаминов на 1 кг корма
		1-го вида x1	2-го вида x2
	9	3	1
	8	1	2
	12	1	6
Цена 1 кг корма		4 руб	6 руб

Стоимость одного килограмма корма 1-го вида 4 руб., 2-го вида – 6 руб. Составить суточный рацион с минимальной стоимостью и с содержанием витаминов не менее требуемого минимума.

Построимэкономико-математическую модель задачи. Обозначим- количество кормов 1-го и 2-го вида. Требования по содержанию витаминов:

(1.1).

По смыслу задачи

(1.2).

Пусть - общая стоимость всего рациона.

В задаче могут присутствовать также ограничения на общий объем смеси и ограничения на количество используемых ингре­диентов.

Введем обозначения:

п —количество исходных ингредиентов;

т —количество компонентов в смеси;

w —количество условий, отражающих содержаниеj-го ингре­диента в смеси;

х_j— количествоj-го ингредиента, входящего в смесь;

а_ij — доляj-го компонента вj-м ингредиенте;

b_i —минимально допустимая доляi-го компонента в смеси;

с_j— стоимость единицыj-го ингредиента;

d_rj— коэффициент, отражающийr-е условие на содержаниеj-го ингредиента в смеси.

Модель В:

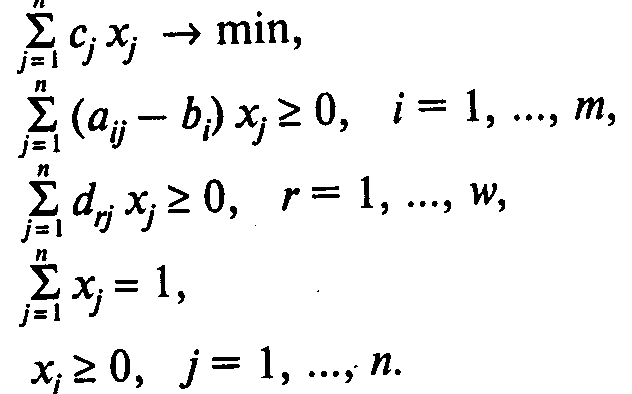
Здесь (4) — целевая функция (минимум затрат на получение смеси);

(5) — группа ограничений, определяющих содержание компонентов в смеси;

(6) — группа ограничении на содержание ингредиентов в смеси;

(7) — ограничение на количество смеси;

(8) — ограничения на неотрицательность переменных.

Ограничения (5) и (6) отличают задачу смешения от задачи оптимального планирования производства. Заметим, что значения правых частей этих ограничений равны нулю.

Вектор х* с компо­нентами, являющийся решением этой оптимизационной зада­чи, называют рецептом приготовления смеси или рецептом сме­шения.

Пример 2.

Сочинский винзавод производит две марки сухого вина: «Чер­ный лекарь» и «Букет роз». Оптовые цены, по которым реализу­ется готовая продукция, соответственно 68 и 57 руб. за литр. Ин­гредиентами для приготовления этих вин являются белое, розо­вое и красное сухие вина, закупаемые в Краснодаре. Эти вина стоят соответственно 70, 50 и 40 руб. за литр. В среднем на со­чинский винзавод поставляется ежедневно 2000 л белого, 2500 л розового и 1200 л красного вина.

В вине «Черный лекарь» должно содержаться не менее 60% белого вина и не более 20% красного.

Вино «Букет роз» должно содержать не более 60% красного и не менее 15% белого.

Определите рецепты смешения ингредиентов для производства вин «Черный лекарь» и «Букет роз», обеспечивающие заводу мак­симальную прибыль.

Решение.Пустьx_kj— количествоj-го ингредиента (j= 1, 2, 3), входящего вk-ю смесь (k =1, 2). Например,x₂₃— количество красного вина, ежедневно используемого для приготовления вина «Букет роз». Тогда модель оптимального смешения имеет следу­ющий вид.

Критерий максимизации прибыли:

(68 - 70)х₁₁ +(68 - 50)x₁₂+ (68 - 40)x₁₃+ (57 - 70)x₂₁+ + (57 - 50)x₂₂+ (57 - 40)x₂₂®max.

Ограничения на поставки ингредиентов:

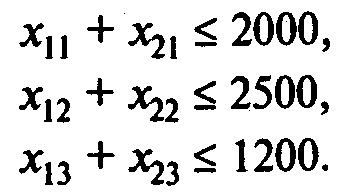
Ограничения, отражающие условия на содержание ингредиен­тов в смеси:

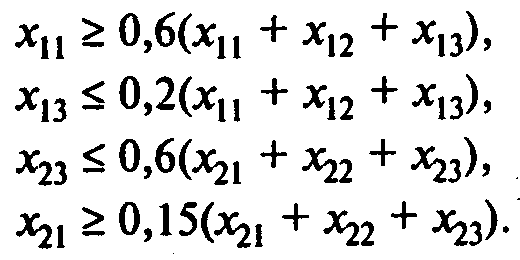
В многопродуктовыхзадачах ингредиенты используют­ся для приготовления не одной, а нескольких смесей. При этом в качестве переменнойx_kj, такой задачи рассматривается количество ингредиентаj, используемое для приготовления смесиk.Крите­рий задачи — максимизация прибыли.

Введем обозначения:

п —количество исходных ингредиентов;

т —количество компонентов в смеси;

w —количество условий, отражающих содержаниеj-го ингре­диента в смеси;

s —количество смесей;

х_kj— количествоj-го ингредиента, входящего вk-ю смесь;

а_ij— доляi-го компонента вj-м ингредиенте;

b_ik —минимально допустимая доляi-го компонента вk-й смеси;

с_j— стоимость единицыj-го ингредиента;

р_k —стоимость единицыk-й смеси;

d_rkj —коэффициент, отражающийr-е условие на содержаниеj-го ингредиента вk-й смеси;

и_j —количество имеющегосяj-го ингредиента.

Модель С:

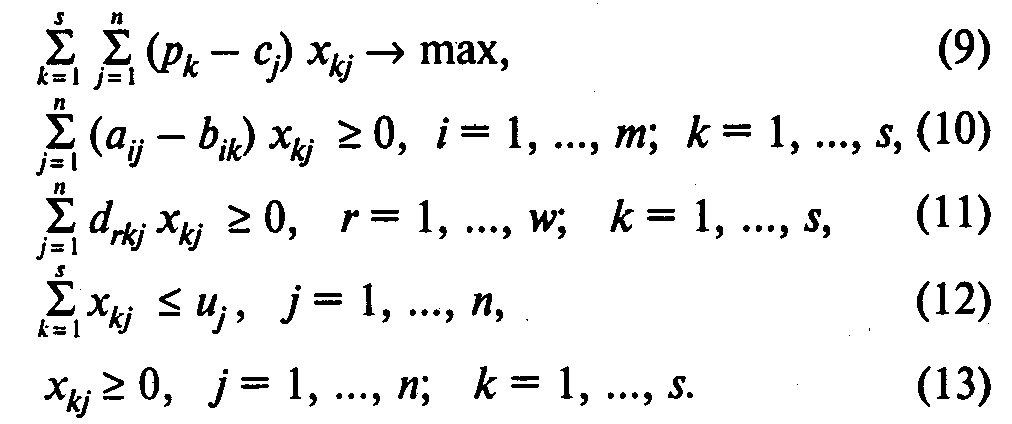
Здесь (9) — целевая функция (максимум прибыли);

(10) — группа ограничений, определяющих содержание компонентов в смеси;

(11) — группа ограничений на содержание ингредиентов в смеси;

(12) — ограничения на количество ингредиентов;

(13)— ограничения на неотрицательность переменных.

3. ЗАДАЧА О РАСПРЕДЕЛЕНИИ ПРОИЗВОДСТВА

Поступил заказ: за время произвестиединиц продукции номенклатурына станках. Пусть:

- производительность–го станка по-ой продукции (число единиц продукции, которое можно сделать на станкев единицу времени);

- затраты на производство продукциина станкев единицу времени.

Составить план суммарной загрузки станков (распределение объемов производства продукции различных типов по станкам) с минимальными затратами.

Построимэкономико-математическую модель задачи. Обозначим- время, в течение которого станокизготавливает продукцию.

Ограничения по времени:

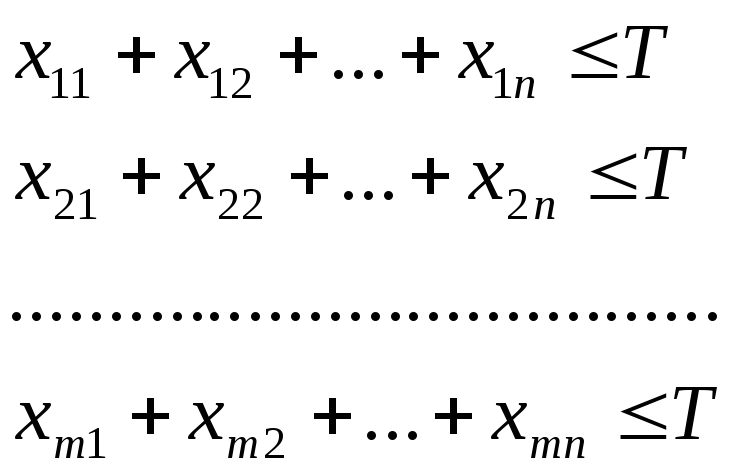(1.1).

Ограничения в соответствии с заказами:

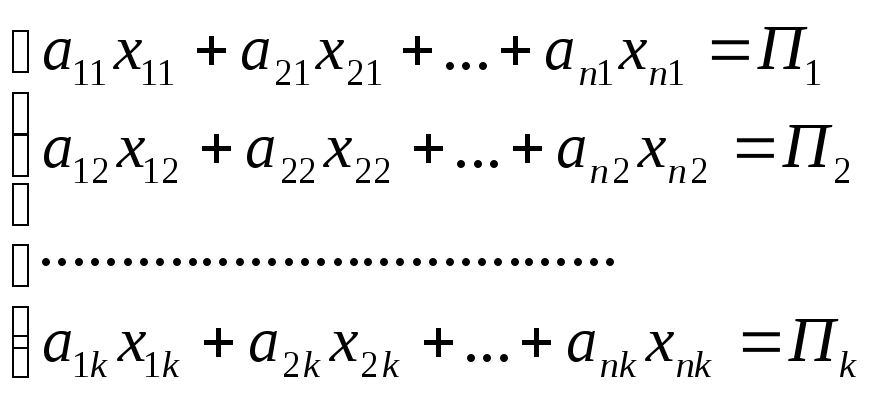
По смыслу задачи

(1.2).

Пусть - общие затраты на производство всей продукции.

4. ЗАДАЧА О РАСКРОЕ

Задача оптимального раскроясостоит в том, что­бы выбрать один или несколько способов раскроя материала и определить, какое количество материала следует раскраивать, при­меняя каждый из выбранных способов. Задачи такого типа воз­никают в металлургии и машиностроении, лесной, лесообрабаты­вающей, легкой промышленности.

Выделяют два этапа решения задачи оптимального раскроя. На первом этапе определяются рациональные способы раскроя мате­риала, на втором — решается задача линейного программирова­ния для определения интенсивности использования рациональных способов раскроя . Определение рациональных способов раскроя материала.

В задачах оптимального раскроя рассматриваются так называемые рациональные (оптимальные по Парето) способы раскроя. Пред­положим, что из единицы материала можно изготовить заготов­ки нескольких видов. Способ раскроя единицы материала назы­вается рациональным (оптимальным по Парето),если увеличение числа заготовок одного вида возможно только за счет сокращения числа заготовок другого вида.

Пусть k —индекс вида заготовки,k =1,....q; i —индекс спо­соба раскроя единицы материала,i= 1,...,р; а_ik —количество (це­лое число) заготовок видаk,полученных при раскрое единицы материала <-м способом.

Приведенное определение рационального способа раскроя мо­жет быть формализовано следующим образом.

Способ раскроя v называется рациональным (оптимальным по Па­рето),если для любого другого способа раскрояiиз соотношенийа_ik ³ а_vk , k= 1, ...,q,следуют соотношенияа_ik = а_vk, k= 1, ...,q.