2. Определение интенсивности использования рациональных спо­собов раскроя.

Обозначения:

j—индекс материала,j= 1,...,п;

k—индекс вида заготовки,k= 1, ...,q;

i —индекс способа раскроя единицы материала,i= 1,...,р;

а_ijk— количество (целое число) заготовок видаk,полученных при раскрое единицыj-го материалаi-м способом;

b_k —число заготовок видаk в комплекте, поставляемом заказ­чику;

d_j —количество материалаj-го вида;

x_ji —количество единицуj-го материала, раскраиваемых поi-му способу (интенсивность использования способа раскроя);

c_ji —величина отхода, полученного при раскрое единицыj-го материала поi-му способу;

у —число комплектов заготовок различного вида, поставля­емых заказчику.

Модель А раскроя с минимальным расходом материалов:

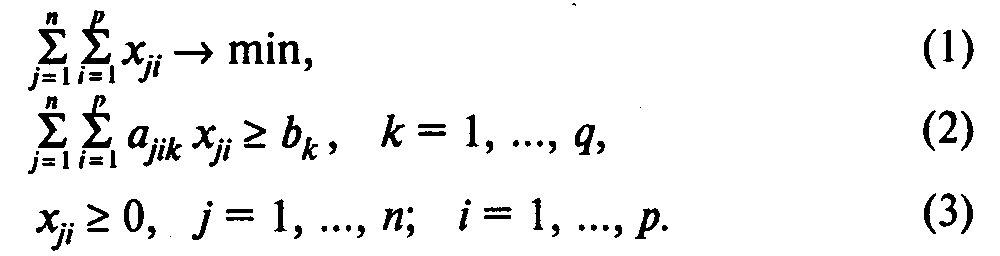
Здесь (1) — целевая функция (минимум количества использу­емых материалов);

(2) — система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;

(3) — условия неотрицательности переменных.

Специфическими для данной области приложения модели ли­нейного программирования являются ограничения (2).

Модель В раскроя с минимальными отходами:

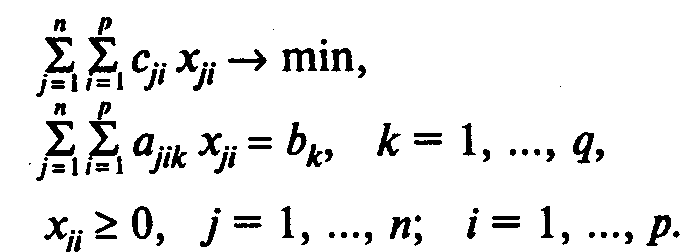
Здесь (4) — целевая функция (минимум отходов при раскрое ма­териалов);

(5) — система ограничений, определяющих количество заготовок, необходимое для выполнения заказа;

(6) — условия неотрицательности переменных.

Модель С раскроя с учетом комплектации:

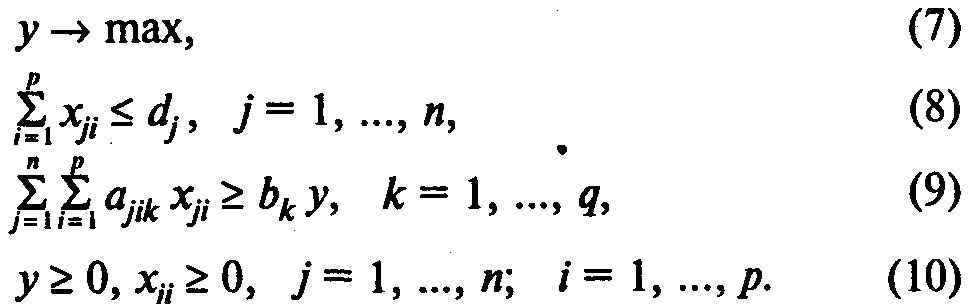
Здесь (7) — целевая функция (максимум комплектов, включающих заготовки различных видов);

(8) — ограничения по количеству материалов;

(9) — система ограничений, определяющих количество заготовок, необходимое для формирования комплектов;

(10) — условия неотрицательности переменных.

Специфическими для данной области приложения модели ли­нейного программирования являются ограничения (9).

Пример 1.Способы раскроя металлического стержня.

Определите все рациональные способы раскроя металлического стержня длиной 100 см на заготовки трех типов: длиной 20, 30 и 50 см. Укажите величину отходов для каждого способа.

Изх этих стержней изготавливают парники. Для одного парника требуется 40 заготовок длиной 50 см, 55 заготовок длиной 30 см и 86 заготовок длиной 20 см. Определить рациональный способ раскроя

Решение.Для данного материала и указанных заготовок су­ществует семь различных рациональных способов раскроя. Все они приведены в следующей таблице:

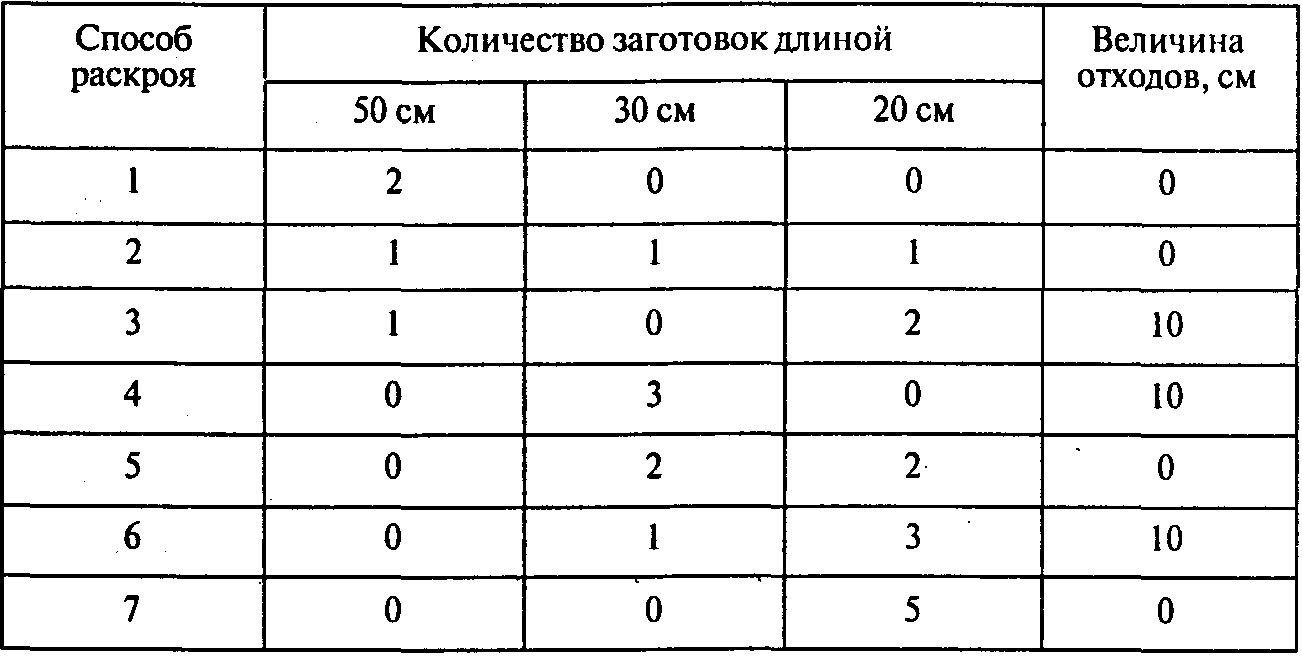
Пример2.Способы раскроя куска кожи.

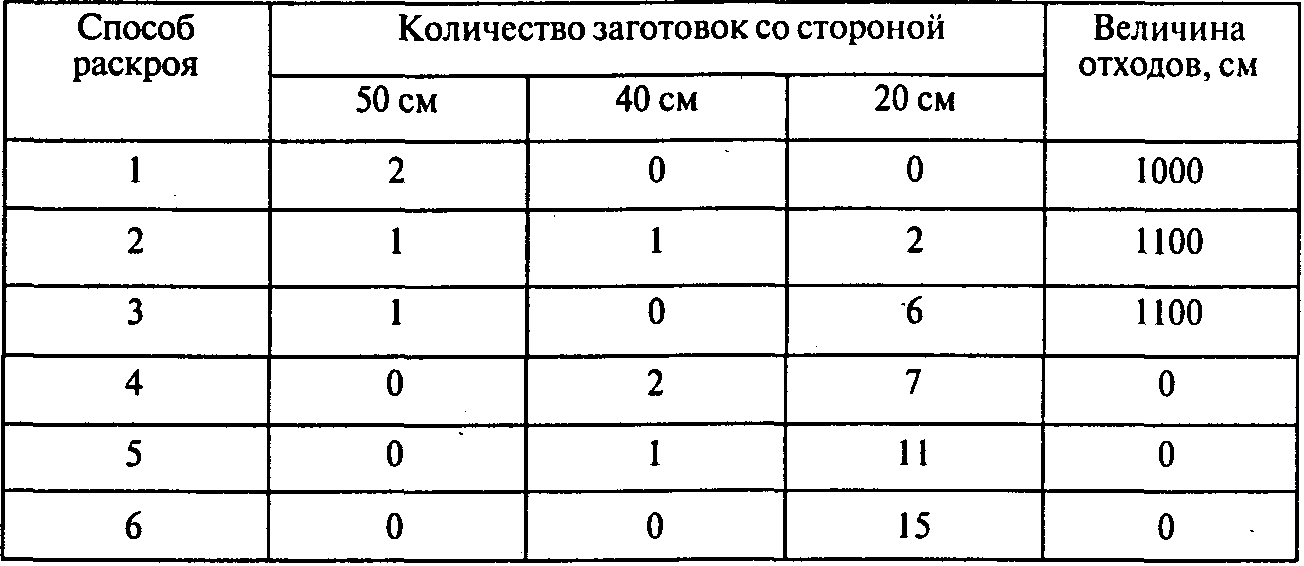
1. Из прямоугольного листа железа размером 100 х 60 см необходимо изготовить квадратные заготовки со сторонами 50,40 и 20 см. Эти заготовки нужны в качестве перегородок при изго­товлении пластмассовых коробок для хранения инструментов. Чтобы сделать одну коробку, нужно иметь четыре заготовки со стороной 50 см, шесть заготовок со стороной 40 см и двенадцать — со стороной 20 см. На складе находится 100 листов материала. Определит рациональный план раскроя с минимальным расходом сырья

.Решение.Для данного материала и указанных заготовок су­ществует шесть различных рациональных способов раскроя:

Пример 3.Изготовление парников из металлических стержней.

При изготовлении парников используется материал в виде ме­таллических стержней длиной 220 см. Этот материал разрезается на стержни длиной 120, 100 и 70 см. Для выполнения заказа тре­буется изготовить 80 стержней длиной 120 см, 120 стержней дли­ной 100 см и 102 стержня длиной 70 см.

Решение.Определяем все рациональные способы раскроя ма­териала на заготовки. Таких способов оказывается пять:

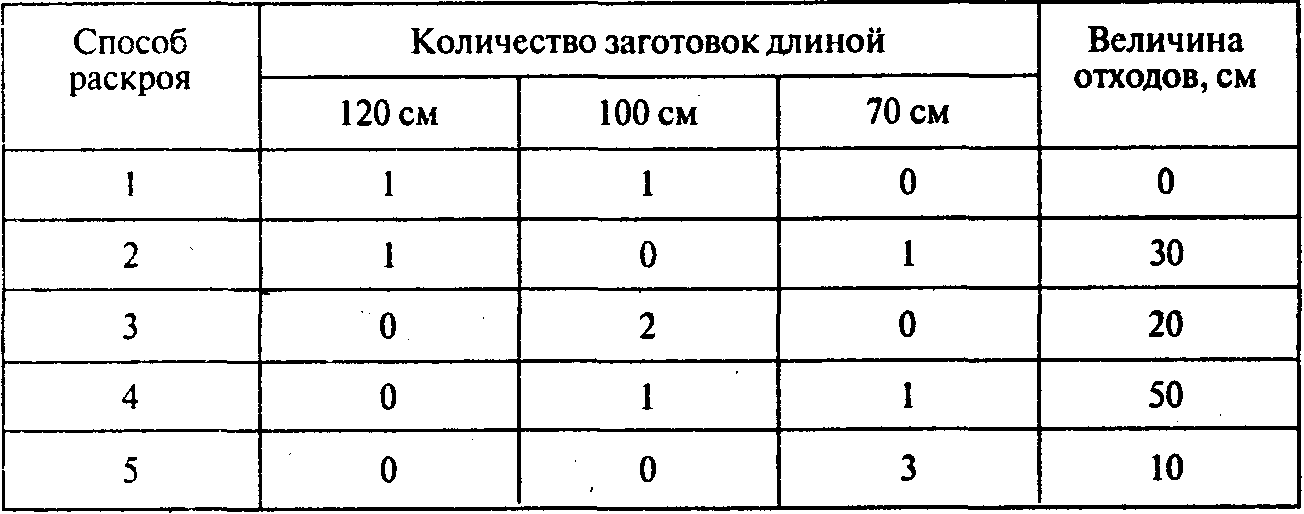
Используем модель Адля одного вида материала. Тогдах_i— количество единиц материала, раскраиваемых поi-му способу.

Для ответа на второй и третий вопросы задачи получаем сле­дующую модель линейного программирования с критерием «ми­нимум общего количества используемого материала»:

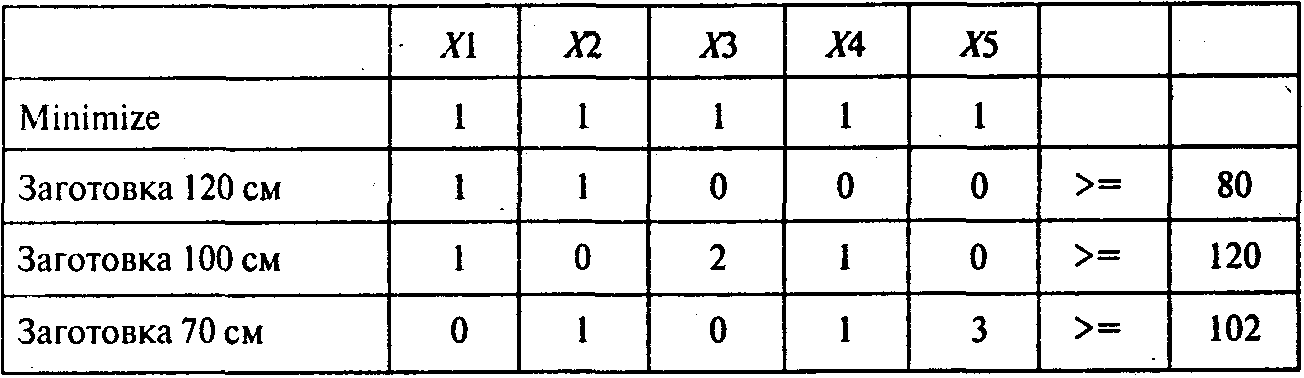
Решая задачу, получаем следующий результат:

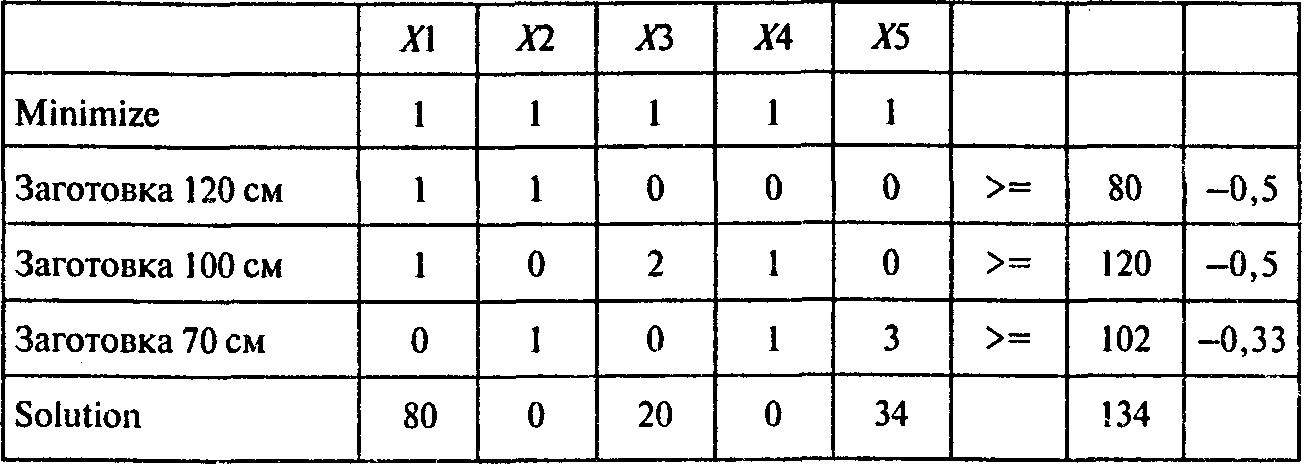
Ответы: 1. Пять способов. 2. 134 единицы материала. 3. Три из пяти рациональных способов раскроя.

2. Графический метод решения задач линейного программирования

Графический метод решения задач линейного программирования в его непосредственной форме применяется только в случае двух переменных.

Пусть требуется найти максимальное значение функции

(1)

при ограничениях

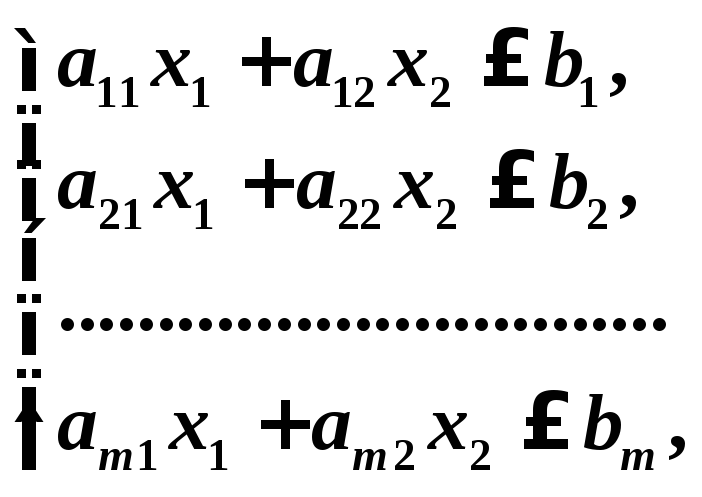(2)

,

где ;;– заданные числа.

Введем на плоскости прямоугольную систему координат . Каждое неравенствозадает полуплоскость с границей.

Чтобы определить, какую именно полуплоскость определяет данное неравенство, достаточно взять произвольную точку плоскости (например, начало координат) и подставить в неравенство числа. Если получим верное числовое неравенство, то полуплоскость, в которой лежит данная точка — искомая. В противном случае нужная полуплоскость лежит по другую сторону прямой.

Область допустимых решений системы ограничений (2) – это область пересечения полуплоскостей, определяемых каждым из неравенств.

Допустим, что область допустимых решений системы ограничений (2) — четырехугольник АВСD (рис. 3).

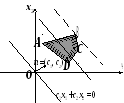
Рассмотрим линейную функцию . При фиксированном значенииполучаем уравнение прямой линии на плоскости.

На рисунке показана прямая, соответствующую уравнению . Эта прямая пройдет через начало координат. Другим значениямбудут соответствовать прямые, параллельные друг другу.

Прямая, уравнение которой получено из целевой функции задачи при равенстве ее постоянной величине, т.е. прямая , называетсялинией уровня целевой функции.

Известно, что коэффициенты при переменных в уравнении прямой на плоскости являются координатами вектора нормали к этой прямой: . Следовательно, нормальный вектор всех линий уровня.

Если перемещать линию уровня параллельно ее начальному положению в направлении вектора (см. рис. 3), то для данного случая последней точкой, в которой линия уровня коснется области допустимых решений, окажется точкаВ.

Линия уровня, имеющая общие точки с областью допустимых решений и расположенная так, что область допустимых решений целиком находится в одной из полуплоскостей, называется опорной прямой.

Теорема.Значения целевой функции в точках линии уровняувеличиваются, если линию уровня перемещать параллельно начальному положению внаправлении вектора нормали,и убывают при перемещении в противоположном направлении.

Таким образом, алгоритмрешения задачи линейного программирования с двумя переменными графическим методом такой:

1. Строится область допустимых решений.

2. Строится вектор 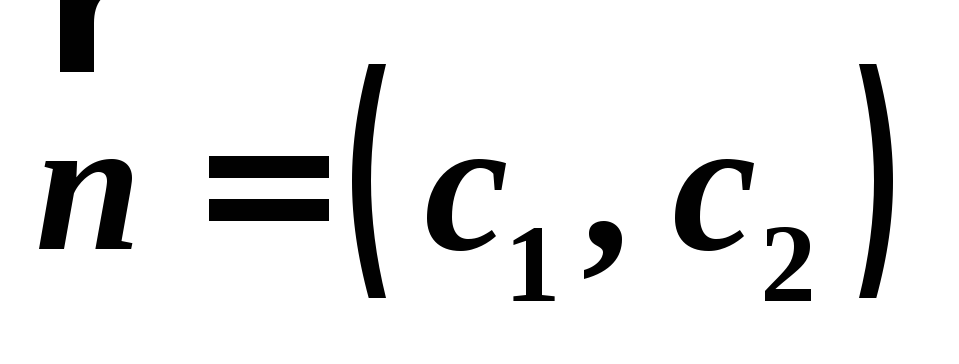с точкой приложения в начале координат.

3. Перпендикулярно вектору 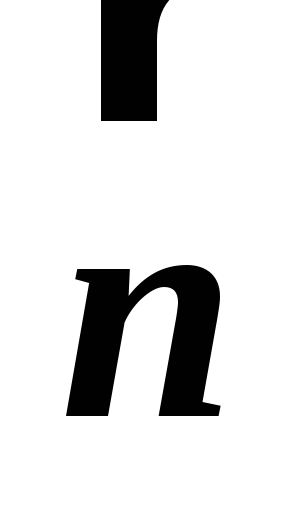проводится одна из линий уровня, соответствующая уравнению.

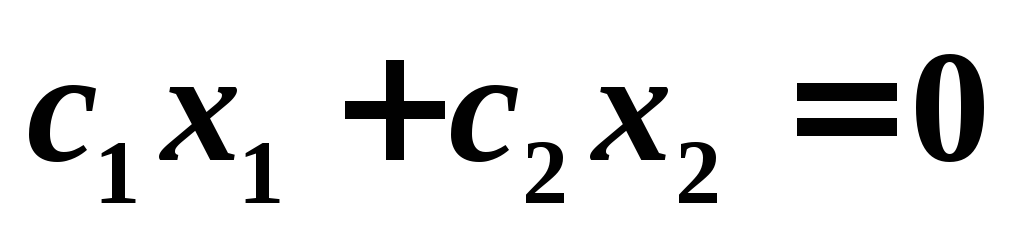4. Линия уровня перемещается до положения опорной прямой. На этой прямой и будет находится максимум или минимум функции.

В зависимости от вида области допустимых решений и целевой функции возможны следующие случаи:

На рис.4,а линия уровня дважды становиться опорной по отношению к многоугольнику решений. Минимальное значение целевая функция достигает в точке В, максимальное — в точкеD. Задача имеет единственное решение.

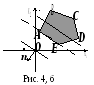
На рис. 4, б максимальное значение целевая функция принимает на опорной прямой, совпадающей со стороной АЕмногоугольника, задача имеет бесконечное множество решений.

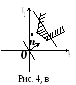
На рис. 4, в область допустимых решений не ограничена в сторону увеличения значений целевой функции, задача не имеет ни одного оптимального решения.

Пример.Решить ЗЛП графическим методом.

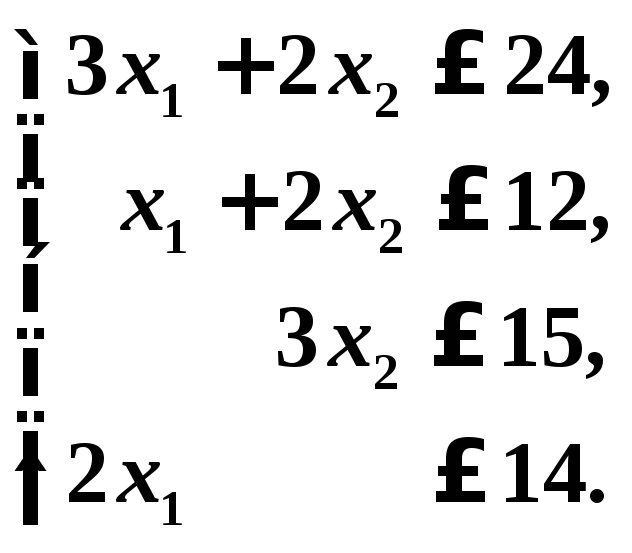или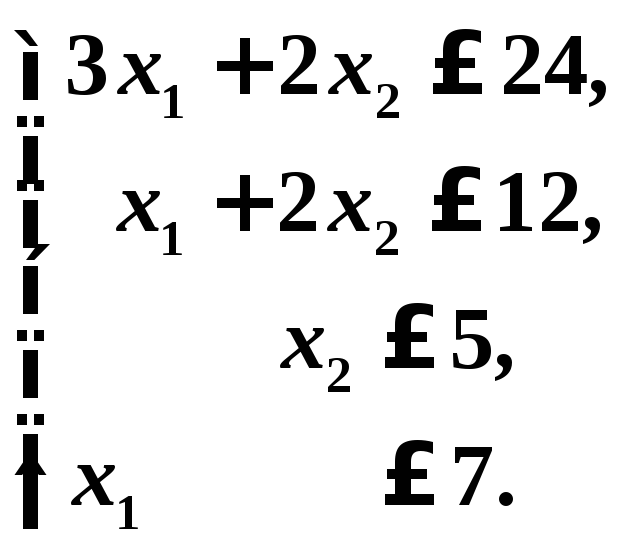

,.,.