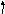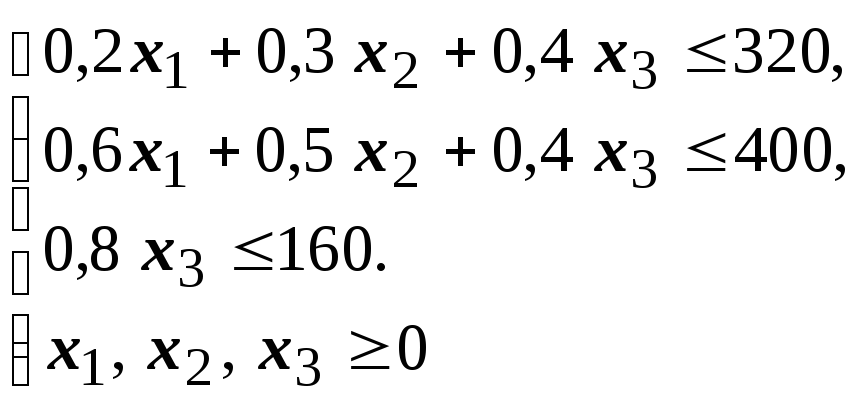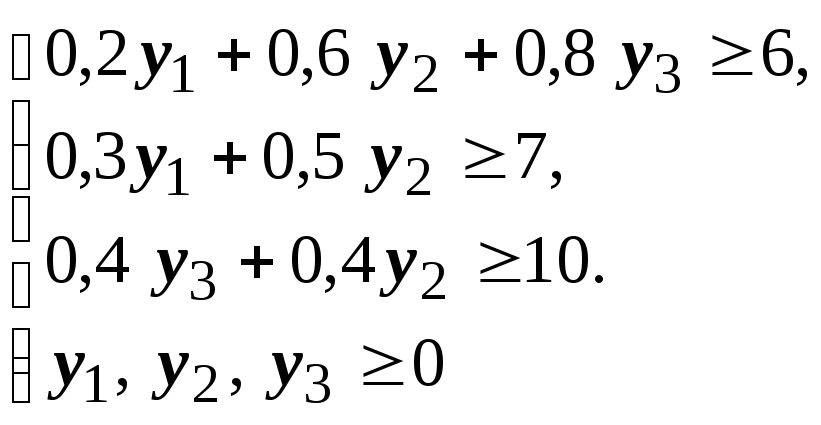- •Содержание Введение
- •2. Определение интенсивности использования рациональных способов раскроя.
- •Решение
- •Решение
- •Решение
- •Решение
- •Решение
- •1. Задание исходных данных задачи
- •2. Вычисление матрицы коэффициентов полных материальных затрат b.
- •3. Проверка продуктивности матрицы а.
- •4. Вычисление вектора валового выпуска X.
- •5. Вычисление межотраслевых поставок продукции xij
Решение
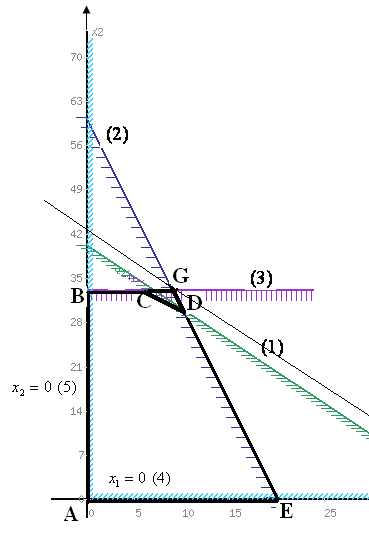
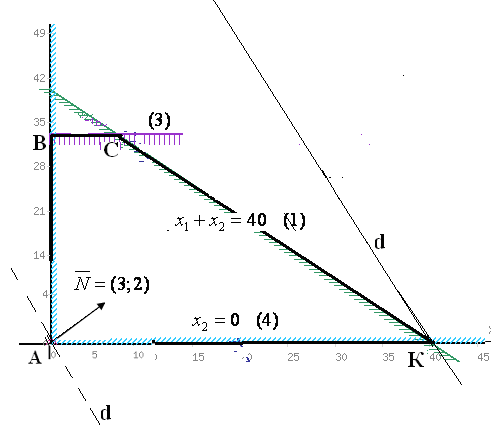
1. Строим область допустимых решений. Уравнения границ области:
Прямые
![]() и
и![]() строим по двум точкам:
строим по двум точкам:
![]()
![]()
![]()
![]()
-
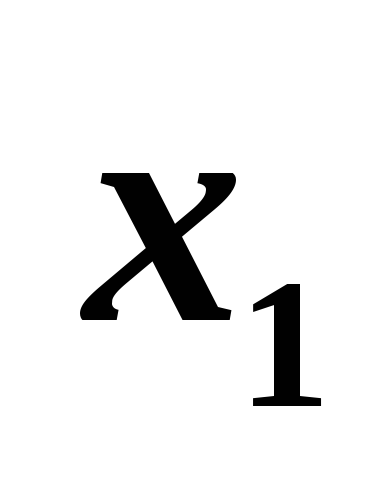
0
8
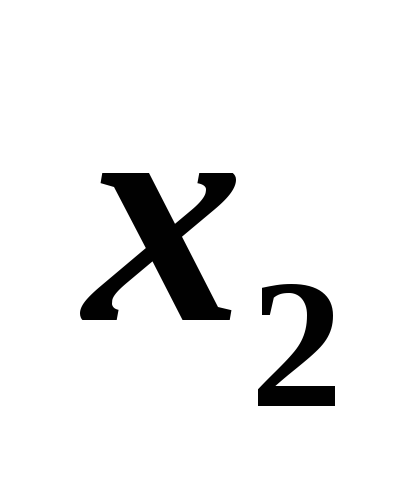
12
0
-
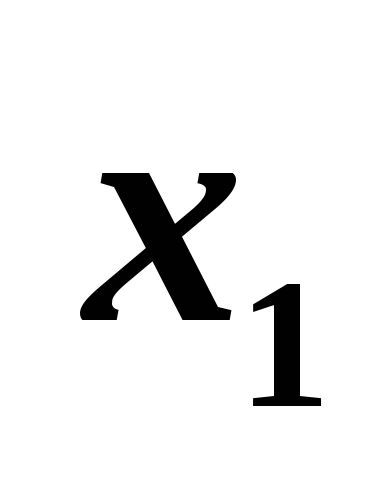
0
12
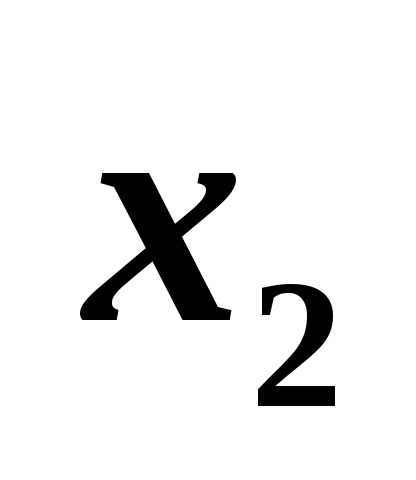
6
0
![]()
![]()
Прямая
![]() разбивает плоскость на две полуплоскости
– одна – выше прямой, другая – ниже
прямой:
разбивает плоскость на две полуплоскости
– одна – выше прямой, другая – ниже
прямой:
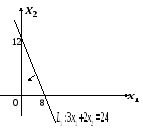
Для определения того, какая именно
полуплоскость задается неравенством
![]() ,
подставим в него координаты точки
,
подставим в него координаты точки![]() :
:![]() - верное неравенство, значит, неравенство
- верное неравенство, значит, неравенство![]() задает полуплоскость, находящуюся
ниже прямой
задает полуплоскость, находящуюся
ниже прямой![]() ,
на что указывает стрелочка на рисунке.
,
на что указывает стрелочка на рисунке.
Прямая
![]() также разбивает плоскость на две
полуплоскости:
также разбивает плоскость на две
полуплоскости:
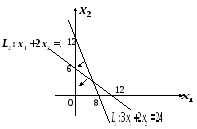
Подставим в неравенство
![]() координаты точки
координаты точки![]() :
:![]() - верное неравенство, значит, неравенство
- верное неравенство, значит, неравенство![]() задает полуплоскость, находящуюся
ниже прямой
задает полуплоскость, находящуюся
ниже прямой![]() ,
что также отмечено стрелочкой на
рисунке.
,
что также отмечено стрелочкой на
рисунке.
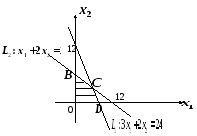
Одновременно обоими неравенствами
задается область четырехугольника
![]() :
:
Учитывая, что
![]() и
и![]() ,
получаем
,
получаем
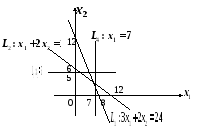
Таким образом, Область допустимых решений — многоугольник ОАВСDЕ:
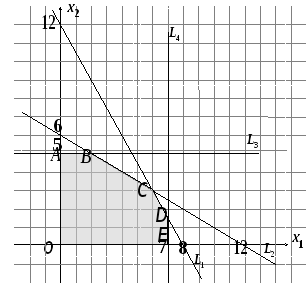
2. Для линии уровня
![]() строим нормальный вектор
строим нормальный вектор![]() :
:
3. Перпендикулярно вектору
![]() строим одну из линий уровня, на рисунке
это прямая
строим одну из линий уровня, на рисунке
это прямая![]() .
.
4. Так как задача на максимум, то перемещаем
линию уровня в направлении вектора
![]() до положения опорной прямой. В данном
случае это прямая, проходящая через
точкуС. ТочкаСявляется
точкой пересечения прямых
до положения опорной прямой. В данном
случае это прямая, проходящая через
точкуС. ТочкаСявляется
точкой пересечения прямых![]() и
и![]() ,
поэтому ее координаты удовлетворяют
уравнениям этих прямых
,
поэтому ее координаты удовлетворяют
уравнениям этих прямых
![]()
Решив полученную систему, получаем
![]() ,
,![]() ,
т.е.
,
т.е.![]() .Это
и будет оптимальное решение данной
задачи, которому соответствует
максимальное значение целевой функции
.Это
и будет оптимальное решение данной
задачи, которому соответствует
максимальное значение целевой функции![]() .
.
Решение задач линейного программирования с помощью симплекс-таблиц
Симплексный метод в настоящее время получил широчайшее практическое применение и стал универсальным методом линейного программирования.
Рассмотрим следующую задачу линейного программирования, заданную в каноническом виде:
![]() ,
(1)
,
(1)
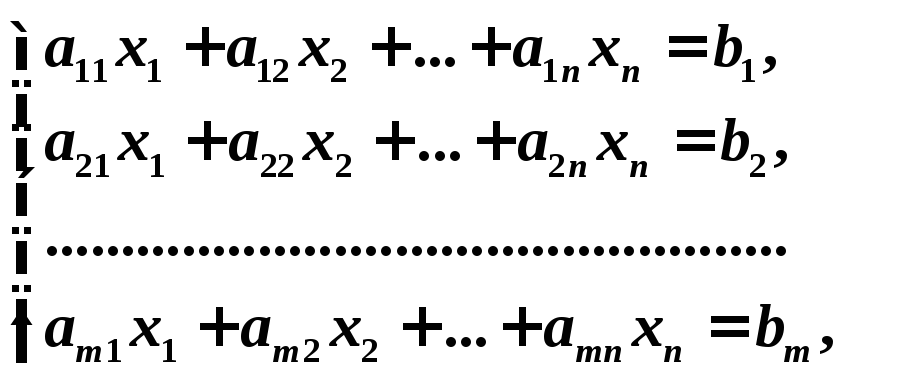 (2)
(2)
![]() ,
,![]() ,
… ,
,
… ,![]() .
.
При решении задачи линейного программирования симплекс-методом требуется, чтобы система уравнений (2) была приведена к допустимому виду, какие-то из переменных —базисныедолжны быть выражены через остальные переменные, которые называютсясвободными, причем в выражениях для базисных переменных свободные члены должны быть неотрицательными.
Например, система
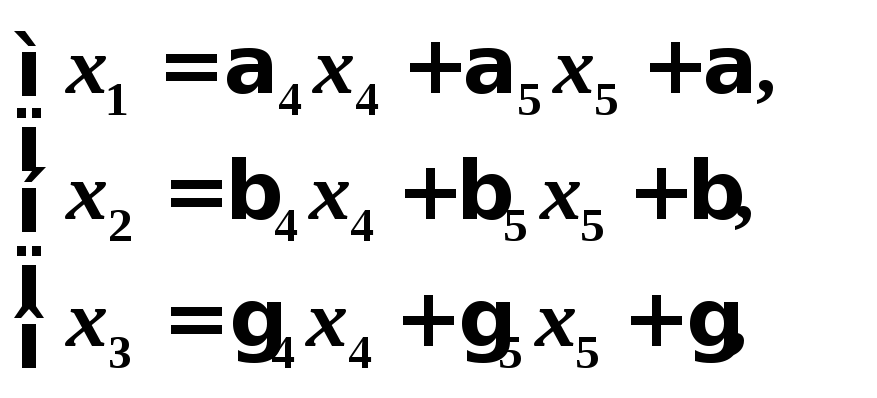 (3)
(3)
где
![]() ,
,![]() ,
,![]() является системой допустимого вида.
является системой допустимого вида.
В этой системе переменные
![]() — базисные. Набор этих переменных
(неизвестных) называетсядопустимым
базисом переменных.
— базисные. Набор этих переменных
(неизвестных) называетсядопустимым
базисом переменных.
Переменные
![]() —
свободные.
—
свободные.
Пусть целевая функция
![]() (4),
а система уравнений приведена к
допустимому виду (3). Заменив в выражении
(4) каждую базисную переменную ее
выражением через свободные переменные,
целевую функцию можно записать в виде:
(4),
а система уравнений приведена к
допустимому виду (3). Заменив в выражении
(4) каждую базисную переменную ее
выражением через свободные переменные,
целевую функцию можно записать в виде:
![]() (5)
(5)
Пусть
![]() .
.
Подставив в систему (3) вместо свободных
переменных
![]() и
и![]() число 0, получим
число 0, получим![]() .
.
Найденное решение системы (3):
![]() (6)
(6)
называется базисным. Это решение
является неотрицательным. Для базисного
решения значение целевой функции![]() .
.
Каждому шагу процесса решения задачи симплекс-методом соответствует своя таблица, таким образом, решение задачи линейного программирования можно представить в виде некоторой последовательности таблиц. Напомним, что рассматривается задача следующего вида:
![]() , (1)
, (1)
при условиях:
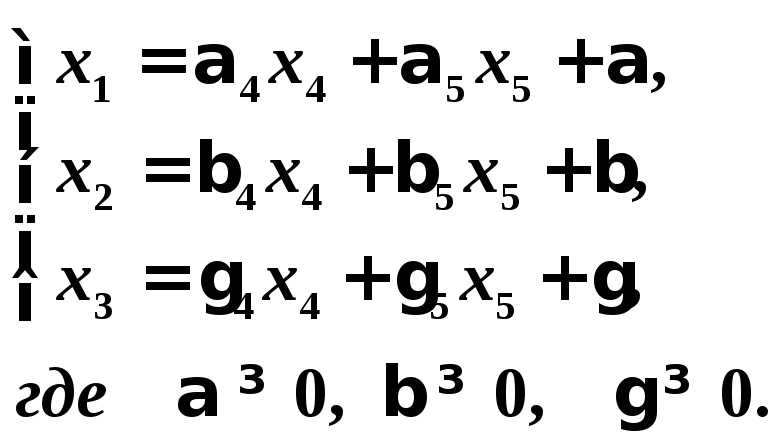 (2)
(2)
Или в допустимом виде:
![]() , (3)
, (3)
при условиях:
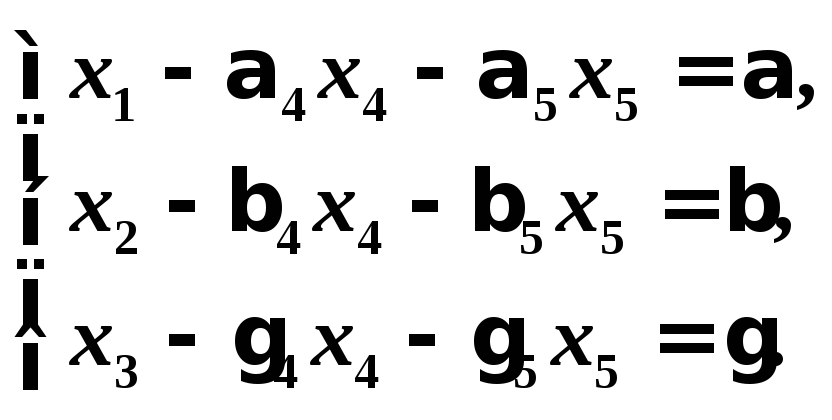 (4)
(4)
Составим первую симплекс-таблицу.
Таблица 4
|
Базисные переменные |
Свободные переменные |
|
|
|
|
|
|
|
α |
1 |
0 |
0 |
-α4 |
-α5 |
|
|
β |
0 |
1 |
0 |
-β4 |
-β5 |
|
|
γ |
0 |
0 |
1 |
-γ4 |
-γ5 |
|
Z |
δ |
0 |
0 |
0 |
- |
-δ5 |
1. Выясним, имеются ли отрицательные
коэффициенты в выражении (1) при переменных
![]() и
и![]() или положительные в выражении (3)
или положительные в выражении (3)![]() ,
то есть являются ли эти коэффициенты
положительными в таблице. Если
положительных коэффициентов в таблице
4 нет, то имеем первый случай, и базисное
решение, отвечающее данному базису,
является оптимальным.
,
то есть являются ли эти коэффициенты
положительными в таблице. Если
положительных коэффициентов в таблице
4 нет, то имеем первый случай, и базисное
решение, отвечающее данному базису,
является оптимальным.
2. Пусть в последней строке имеется
положительное число, например, -
![]() .
Отметим столбец, в котором оно находится,
вертикальной стрелкой. Если все числа
в этом столбце отрицательные, то имеем
второй случай, и задача решения не имеет.
.
Отметим столбец, в котором оно находится,
вертикальной стрелкой. Если все числа
в этом столбце отрицательные, то имеем
второй случай, и задача решения не имеет.
3. Пусть в столбце, отмеченном стрелкой,
имеются положительные числа, то имеем
третьей случай, и надо сделать шаг.
Пусть, например,
![]() и
и![]() ,
находим
,
находим![]() и
и![]() ,
а затем выбираем из них наименьшее.
Пусть это будет
,
а затем выбираем из них наименьшее.
Пусть это будет![]() .
Отмечаем горизонтальную строку, в
которой находится число
.
Отмечаем горизонтальную строку, в
которой находится число![]() ,
горизонтальной стрелкой.
,
горизонтальной стрелкой.
Элемент таблицы, стоящий на пересечении отмеченных столбца и строки, называется разрешающим.
4. Перестраиваем таблицу. Для этого
умножаем выделенную строку на такое
число, что бы на месте разрешающего
элемента появилась 1, то есть на
![]() .
Полученные результаты записываем в
новой таблице в той же строке. Затем к
каждой из оставшихся строк таблицы 4,
включая последнюю строку, прибавляем
вновь полученную строку, умноженную на
такие числа, чтобы в клетках отмеченного
столбца появились нули. Полученные
результаты записывают в новую таблицу.
.
Полученные результаты записываем в
новой таблице в той же строке. Затем к
каждой из оставшихся строк таблицы 4,
включая последнюю строку, прибавляем
вновь полученную строку, умноженную на
такие числа, чтобы в клетках отмеченного
столбца появились нули. Полученные
результаты записывают в новую таблицу.
5. К новой таблице применяется тот же метод. Ее анализируют на первый случай, второй случай и третий случай. В третьем случае строится еще одна таблица. Процесс продолжается до тех пор, пока не придем к первому или второму случаю.
Пример 1.Определить минимальное
значение функции![]() при условиях
при условиях
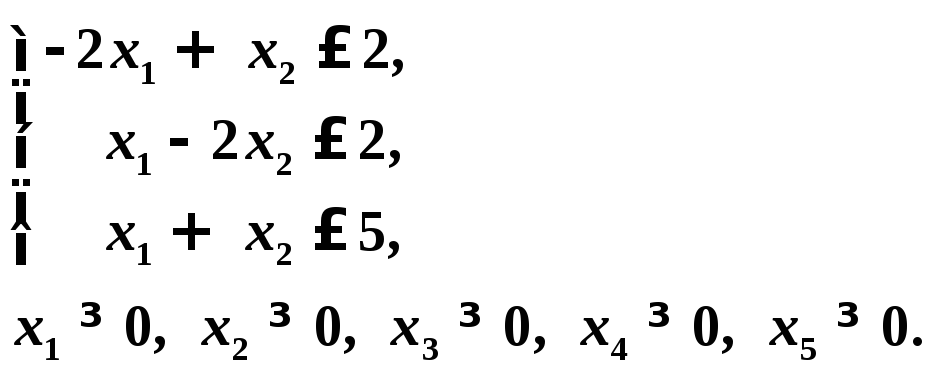
Решение
Запишем задачу в каноническом виде:
![]()
при условиях:
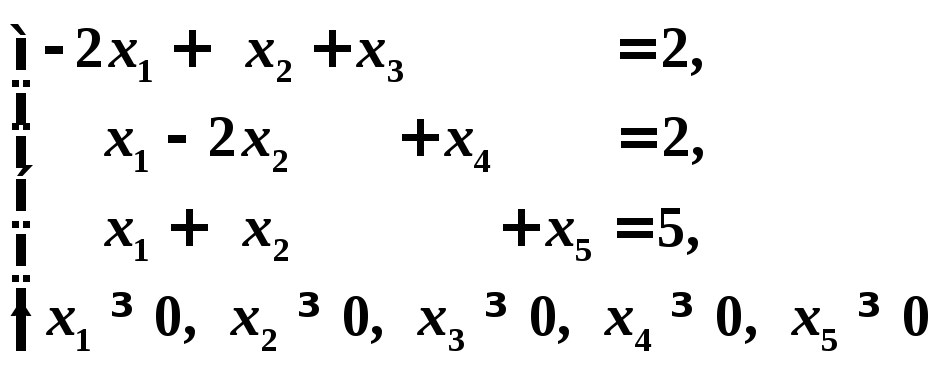
Расширенная матрица
![]() системы:
системы:
![]() =
=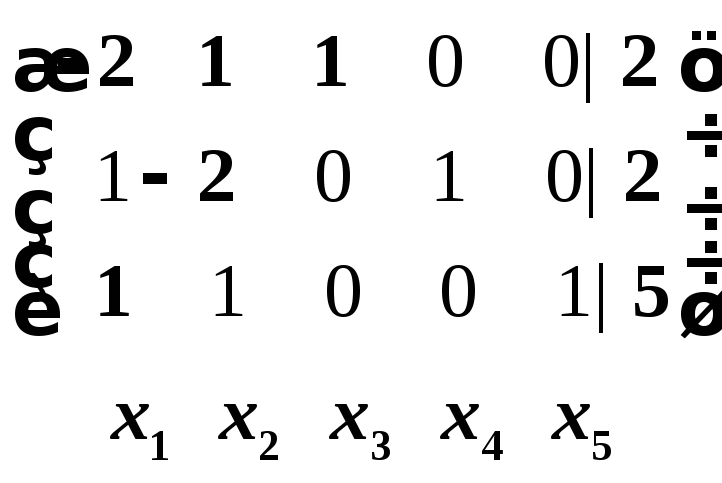 ~
~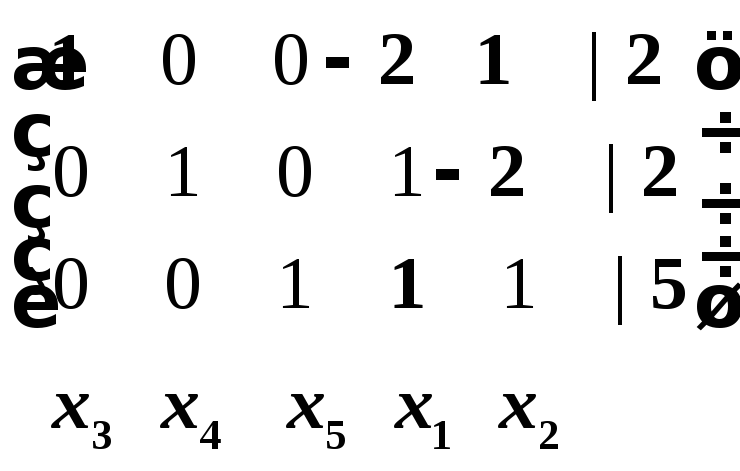 ,
,
Таким образом,
![]() ,
и в системе три базисных переменных -
,
и в системе три базисных переменных -![]() и две свободных -
и две свободных -![]() .
.
Приведем систему к допустимому виду, выразив базисные переменные через свободные:
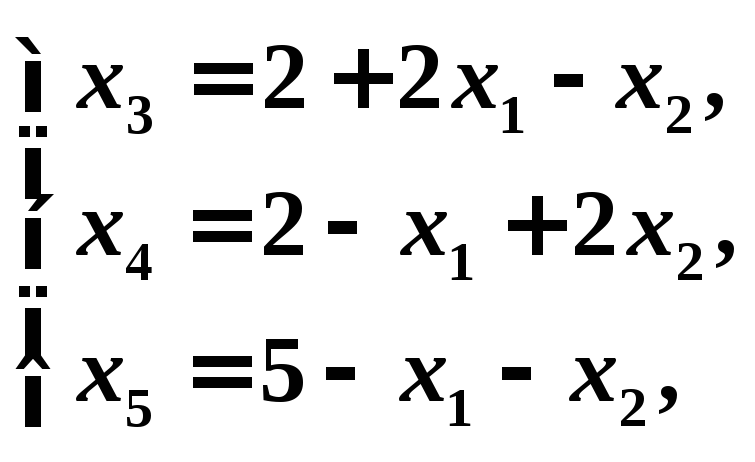 (5)
(5)
Целевая функция изначально оказалась
записанной только через свободные
переменные:
![]() (поэтому выражения (5) нам не пригодились).
(поэтому выражения (5) нам не пригодились).
Система уравнений
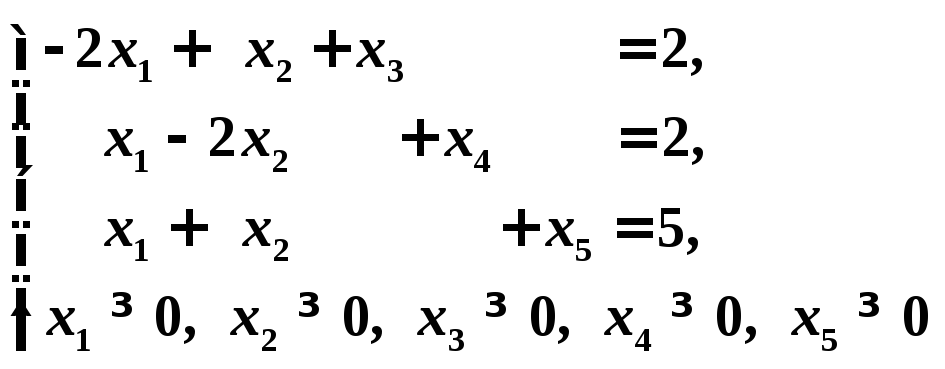
записана в том виде, в каком будем ее
использовать при составлении таблицы.
Из выражения для целевой функции получим
следующее равенство
![]() (эти
коэффициенты при переменных вносятся
в нижнюю строку таблицы).
(эти
коэффициенты при переменных вносятся
в нижнюю строку таблицы).
Заполним таблицу 1.
Таблица 1
|
Базисные переменные |
Свободные члены |
|
|
|
|
|
Отно- шение |
|
|
2 |
-2 |
1 |
1 |
0 |
0 |
- |
|
|
2 |
|
-2 |
0 |
1 |
0 |
|
|
|
5 |
1 |
1 |
0 |
0 |
1 |
|
|
Z |
0 |
1 |
-1 |
0 |
0 |
0 |
|
В последней строке есть положительный
коэффициент – это коэффициент в столбце
![]() .
Выделим этот столбец стрелочкой, этот
столбец называетсяразрешающим
столбцом. (Если положительных
коэффициентов в последней строке
несколько, выбирают столбец с наибольшим
коэффициентом). В разрешающем столбце
имеются положительные числа (в строках
2 и 3 этого столбца). Находим отношение
свободных членов к элементам разрешающего
столбца
.
Выделим этот столбец стрелочкой, этот
столбец называетсяразрешающим
столбцом. (Если положительных
коэффициентов в последней строке
несколько, выбирают столбец с наибольшим
коэффициентом). В разрешающем столбце
имеются положительные числа (в строках
2 и 3 этого столбца). Находим отношение
свободных членов к элементам разрешающего
столбца![]() и
и![]() .
Так как2 < 5, то выделяем горизонтальной
стрелкой строку при базисной переменной
.
Так как2 < 5, то выделяем горизонтальной
стрелкой строку при базисной переменной![]() .
Разрешающим элементом является1
(находится в кружочке).
.
Разрешающим элементом является1
(находится в кружочке).
Заполним таблицу 2.В базисных
переменных![]() заменится на
заменится на![]() .
Для этого умножаем выделенную строку
на
.
Для этого умножаем выделенную строку
на![]() и записываем результат вместо этой
строки.
и записываем результат вместо этой
строки.
Таблица 2
|
Базисные переменные |
Свободные переменные |
|
|
|
|
|
Отно- шение |
|
|
6 |
0 |
-3 |
1 |
2 |
0 |
- |
|
|
2 |
1 |
-2 |
0 |
1 |
0 |
|
|
|
3 |
0 |
3 |
0 |
-1 |
1 |
|
|
Z |
-2 |
0 |
1 |
0 |
-1 |
0 |
|
Умножаем вторую строку таблицы 2 и
складываем с соответствующими значениями
первой строки таблицы 1. Результат
записываем в первую строку таблице 2. В
столбце при переменной
![]() появился ноль. Далее умножаем вторую
строку таблицы 2 на-1и складываем
с соответствующими значениями третьей
строки таблицы 1 и результат записываем
в третьей строке таблицы 2. В столбце
при переменной
появился ноль. Далее умножаем вторую
строку таблицы 2 на-1и складываем
с соответствующими значениями третьей
строки таблицы 1 и результат записываем
в третьей строке таблицы 2. В столбце
при переменной![]() снова появляется ноль.
снова появляется ноль.
Умножаем вторую строку таблицы 2 на -1и складываем с соответствующими
значениями четвертой строки таблицы
1 и результат записываем в четвертой
строке таблицы 2. В столбце при переменной![]() снова появился ноль.
снова появился ноль.
В последней строке есть положительное
число – коэффициент в столбце при
переменной
![]() .
Отметим этот столбец вертикальной
стрелкой. Положительным является также
число в третьей строке, выделяем эту
строку горизонтальной стрелкой.
Разрешающим элементом является3.
.
Отметим этот столбец вертикальной
стрелкой. Положительным является также
число в третьей строке, выделяем эту
строку горизонтальной стрелкой.
Разрешающим элементом является3.
Заполняем таблицу 3.
Умножаем выделенную строку на
![]() и записываем результат вместо этой
строки.
и записываем результат вместо этой
строки.
Таблица 3
|
Базисные переменные |
Свободные переменные |
|
|
|
|
|
|
|
9 |
0 |
0 |
1 |
1 |
1 |
|
|
4 |
1 |
0 |
0 |
1/3 |
2/3 |
|
|
1 |
0 |
1 |
0 |
-1/3 |
1/3 |
|
Z |
-3 |
0 |
0 |
0 |
-2/3 |
-1/3 |
Третью строку таблицы умножаем на 3и складываем с первой строкой, умножаем на2и складываем со второй строкой, умножаем на-1и складываем с четвертой строкой таблицы 2.
В таблице 3 последняя строка не имеет положительных чисел в последних пяти столбцах. Значит, достигнуто оптимальное решение.
Базисные переменные
![]() ,
,![]() ,
,![]() .
Следовательно, базисным решением
являются соответствующие свободные
члены в первой, второй и третьей строках.
Базисное решение для свободных переменных
.
Следовательно, базисным решением
являются соответствующие свободные
члены в первой, второй и третьей строках.
Базисное решение для свободных переменных![]() ,
,
![]() равно нулю. Таким образом, оптимальное
решение имеет вид
равно нулю. Таким образом, оптимальное
решение имеет вид
![]() =4,
=4,![]() =1,
=1,![]() =9,
=9,![]() =0,
=0,![]() =0.
=0.
Минимальным значением целевой функции
является свободный член в последней
строке
![]()
Пример 2. Найти максимальное значение функции:
![]()
при условиях:
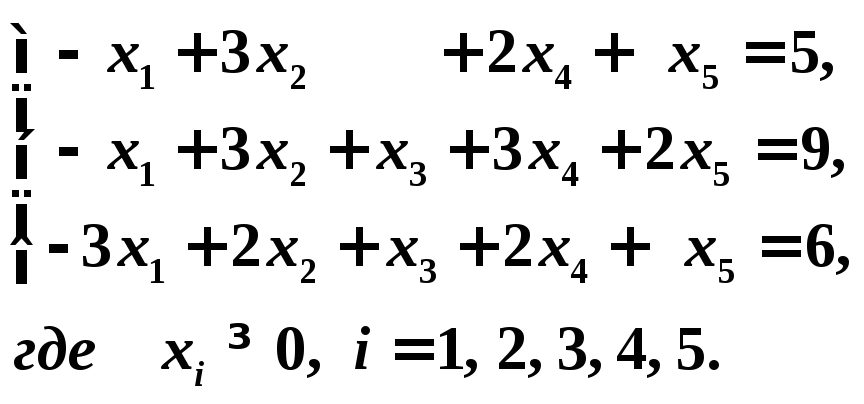
Решение
Сведем задачу на максимум к задаче на минимум. Для этого целевую функцию умножим на (-1):
![]() .
.
Для решения задачи симплекс-методом приведем систему уравнений к допустимому виду.
Запишем расширенную матрицу системы уравнений и приведем ее к трапециевидному виду:
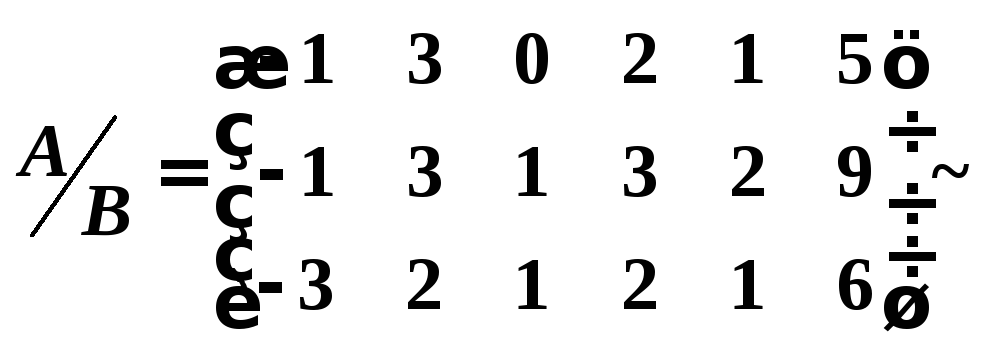




![]() .
.
Следовательно, система уравнений совместна и неопределенная.
По матрице трапециевидного вида восстановим систему:
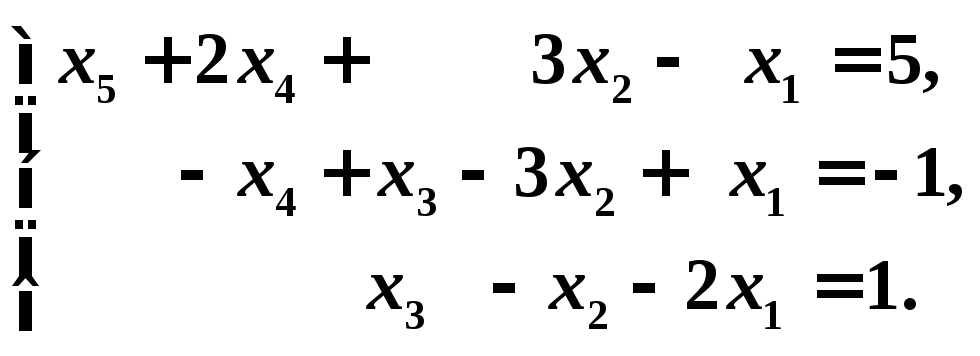
Переменные
![]() ,
,![]() ,
,![]() - базисные,
- базисные,![]() ,
,![]() - свободные. Выражаем базисные переменные
через свободные:
- свободные. Выражаем базисные переменные
через свободные:
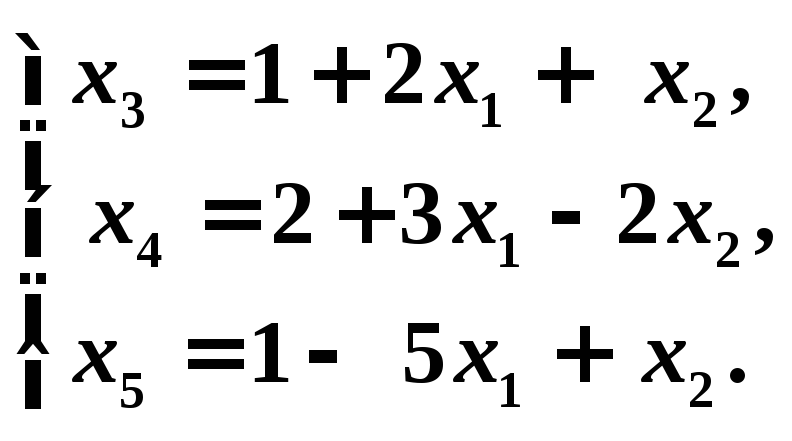
Получим систему уравнений допустимого вида.
Выразим целевую функцию
![]() через свободные переменные:
через свободные переменные:
![]()
Таким образом, задачу можно сформулировать следующим образом:
![]()
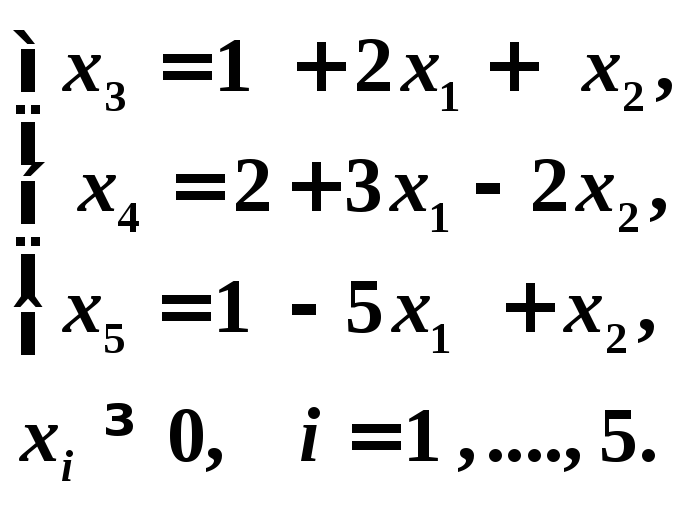
Для составления первой симплекс - таблицы запишем задачу в виде:
![]()
при условиях:

Заполним первую симплекс-таблицу.
Таблица 1
|
Базисные переменные |
Свободные члены |
|
|
|
|
|
Отно- шение |
|
|
1 |
-2 |
- |
1 |
0 |
0 |
- |
|
|
2 |
-3 |
|
0 |
1 |
0 |
|
|
|
1 |
5 |
-1 |
0 |
0 |
1 |
- |
|
Z1 |
-12 |
-18 |
5 |
0 |
0 |
0 |
|
В последней строке есть положительный
коэффициент в столбце переменной
![]() .
Положительным является также число в
строке базисной переменной
.
Положительным является также число в
строке базисной переменной![]() .
Разрешающим элементом является 2.
.
Разрешающим элементом является 2.
Строим вторую таблицу. Для этого умножаем
выделенную стрелкой строку на дробь
![]() и записываем результат вместо этой
строки в новую таблицу (таблица 2).
и записываем результат вместо этой
строки в новую таблицу (таблица 2).
Умножаем вторую строку новой таблицы на 1 и складываем с первой, умножаем на 1 и складываем с третьей, умножаем на -5 и складываем с четвертой строкой старой таблицы.
Таблица 2
|
Базисные переменные |
Свободные члены |
|
|
|
|
|
|
|
2 |
-7/2 |
0 |
1 |
½ |
0 |
|
|
1 |
-3/2 |
1 |
0 |
½ |
0 |
|
|
2 |
7/2 |
0 |
0 |
½ |
1 |
|
Z1 |
-17 |
-21/2 |
0 |
0 |
-5/2 |
0 |
В новой таблице последняя строка не
имеет положительных чисел в последних
пяти столбцах. Значит, достигнуто
оптимальное решение. Базисным решением
для переменных
![]() ,
,![]() ,
,![]() являются соответствующие свободные
члены. Базисное решение для свободных
переменных
являются соответствующие свободные
члены. Базисное решение для свободных
переменных![]() ,
,![]() равно нулю. Таким образом, оптимальное
решение имеет вид:
равно нулю. Таким образом, оптимальное
решение имеет вид:
![]() =0,
=0,![]() =1,
=1,![]() =2,
=2,![]() =0,
=0,![]() =2,
=2,
![]() ,
,
![]() .
.
Реализация симплекс-метода на компьютере
Пример 4.1.Фирма выпускает три вида кожаных изделийA, BиC. На изготовление единицы продукцииAзатрачивается 0,2 ч работы дубильного участка, 0,6 ч раскройного участка, 0 ч завершающего участка. На изготовление единицы продукцииB– 0,3; 0,5 и 0 ч; на изготовление единицы продукцииC– 0,4; 0,4 и 0,8 соответственно. Прибыль от единицы продукции видаAсоставляет 6 ден.ед., видаB– 7 ден.ед., видаC– 10 ден.ед. В течение месяца рабочее время каждого участка ограничено следующим образом:
Дубильного участка – 320 ч; Раскройного участка – 400 ч; Завершающего участка – 160 ч.
Требуется:
записать данные задачи в таблицу;
составить экономическую модель;
Решить задачу с помощью надстройки «Поиск решения»
.
Решение.
Составим таблицу.
Ресурсы ( ч )
Потребление ресурсов на единицу продукции
Ограничения на ресурсы ( ч )
А
В
С
Дубильный участок
0,2
0,3
0,4
320
Раскройный участок
0,5
0,5
0,4
400
Завершающий участок
0
0
0,8
160
Прибыль (ден.ед.)
6
7
10
Экономическая модель.
Пусть выпускается ![]() штук
изделий вида A,
BиC
соответственно. Тогда прибыль от
продажи всех изделий
штук
изделий вида A,
BиC
соответственно. Тогда прибыль от
продажи всех изделий![]() ,
и
,
и
![]()
Ограничения по запасам ресурсов:
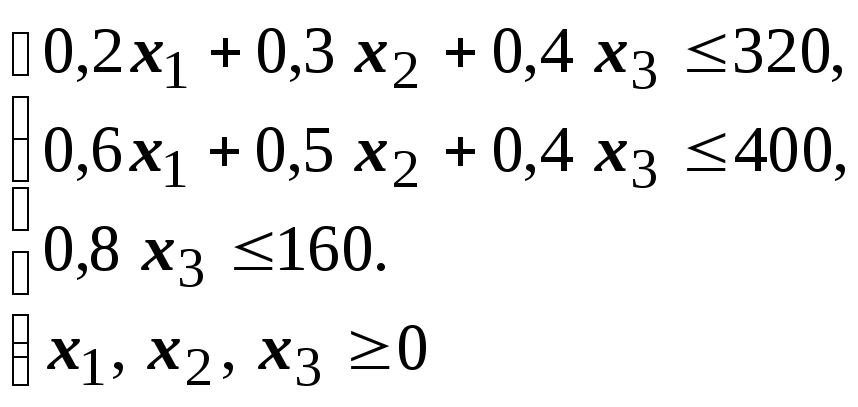
|
Прямая задача линейного программирования |
Двойственная задача |
|
|
|
Решение задачи на компьютере с помощью надстройки «Поиск решения». Соответствующая кнопка должна находиться
Установка приложения к ППП Excel пакета «Поиск решения».
Для WINDOWS-3
Открыть файл Excel. В меню «Сервис» выбрать «Надстройки», установить отметку в строке «Поиск решения»
Для WINDOWS-7
Откройте файл Excel
Нажмите «Кнопку офис» в левом верхнем углу экрана
Появится вкладка:
Нажать «Параметры Excel»
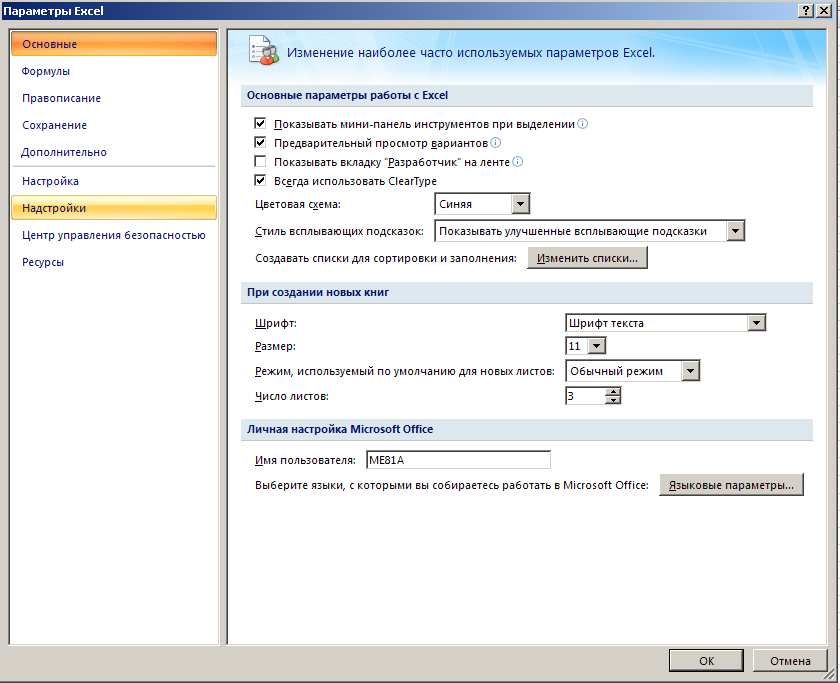
Нажать «Надстройки»
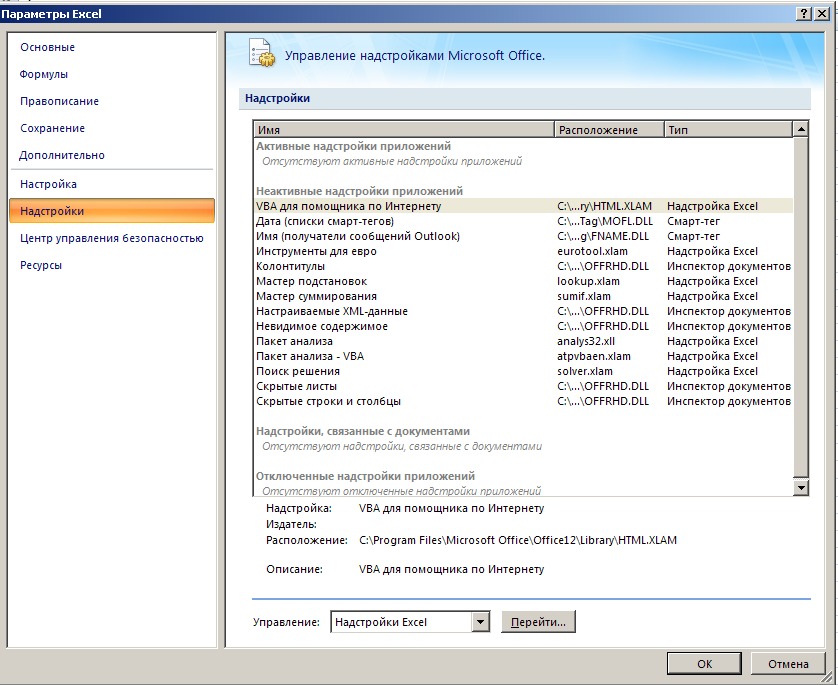
Нажать «Перейти»
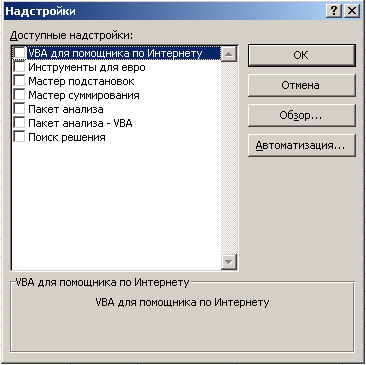
Поставьте отметку в строке «Поиск решения»
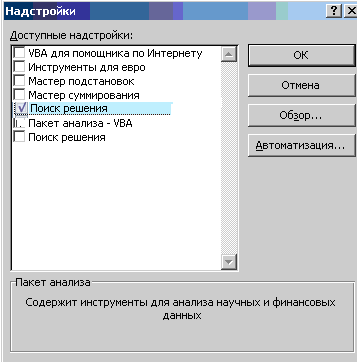
OK
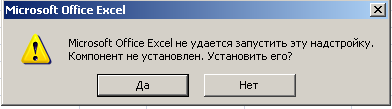
«ДА»
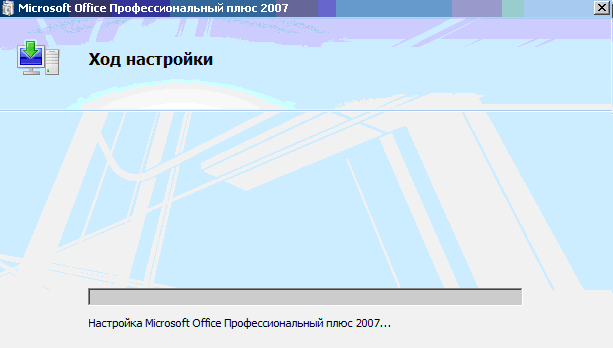
После завершения настройки на вкладке «Данные» появляется кнопка «Поиск решения».

Создадим экранную форму для решения задачи с помощью надстройки «Поиск решения».
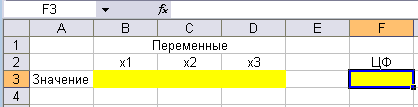
В ячейки B1,C1,D1 запишем обозначения переменных, ячейкиB3,C3,D3 служат для машинного подбора их значений, при которых достигается максимум прибыли. Эти ячейки называются изменяемыми.
В ячейке F3 машина вычислит максимальную прибыль при разработанном плане производства изделий.
В ячейки B4,C4,D4 запишем коэффициенты целевой функции

а в ячейки B6 –D8 - коэффициенты при соответствующих переменных из системы ограничений:

В ячейки G6-G8 внесем запасы ресурсов, а в ячейкиF6-F8 – знаки ограничений

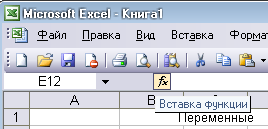
В ячейку F3 введём зависимость
(формулу![]() ) для целевой функции. Для этого щелкнем
курсором на ячейкуF3 ,
затем на панели щелкнем кнопку
) для целевой функции. Для этого щелкнем
курсором на ячейкуF3 ,
затем на панели щелкнем кнопку![]() - вставка функции:
- вставка функции:
на экране появляется диалоговое окно Мастер функций шаг 1 из 2.
В категории на «Математические» выберем функцию СУММПРОИЗВ
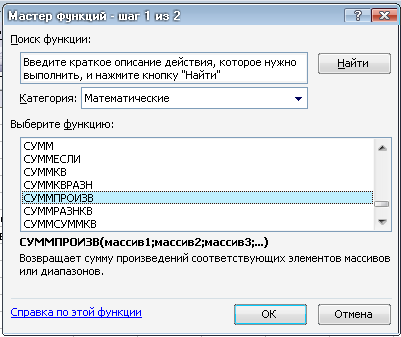
ОК
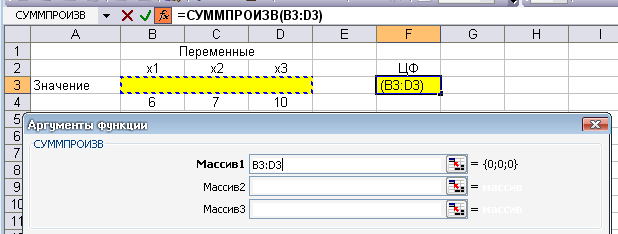
В появившемся окне СУММПРОИЗВ курсором щелкнуть по строке Массив 1и выделить курсором полеB3-D3 изменяемых переменных.
Затем курсором щелкнуть по строке Массив 2и выделить курсором полеB4 -D4
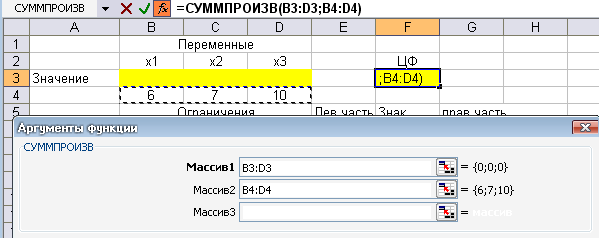
ОК.
В ячейке F3 появится 0

Введём зависимости для ограничений (левые части неравенств). Для этого
Поставим курсор в ячейку Е6 и снова вызовем вставку функции, а через нее - функцию СУММПРОИЗВ. В строке Массив 1выделить ячейкиB3-D3, нажать на клавиатуре клавишуF4. После чего ячейкаF4 будет зафиксирована и не будет «сползать» при протягивании курсора:
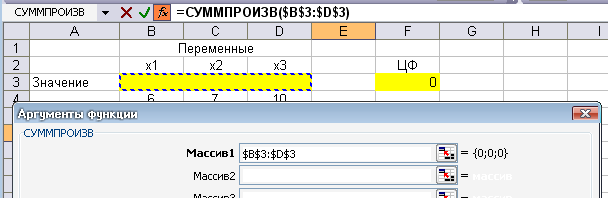
В строке Массив 2выделить первую строчку ограничений (ячейкиB6-D6)
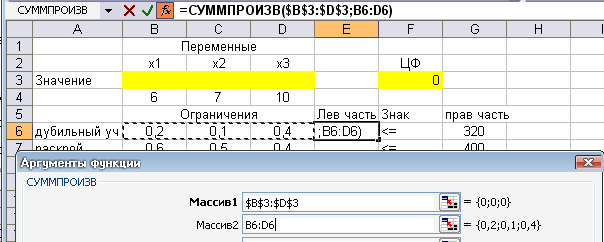
ОК.
После этого в ячейке Е6 появится 0:
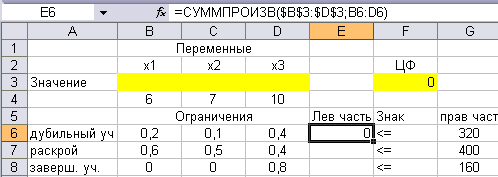
Установите курсор в правый нижний угол ячейки Е6, получите крестик и протяните его вниз по ячейкам Е7 и Е8
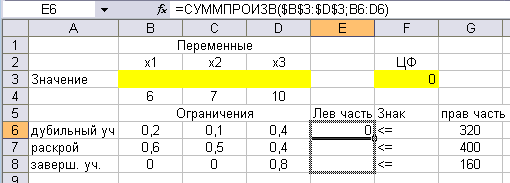
После этого в ячейках Е7 и Е8 тоже появятся нули:
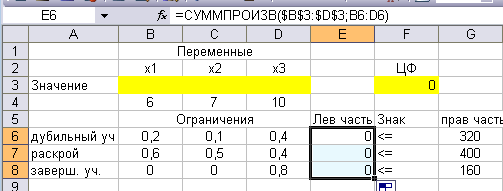
Можно проверить правильность ввода данных в формулах. У нас формулы набраны в ячейке F3 для целевой функции и в ячейкахE6-E8 для ограничений. Поставьте курсор, например, на ячейкуF3 и дважды щелкните. На экране цветом выделятся введенные ячейки:

Нажмите «Enter» или просто щелкните любую пустую ячейку.
Можно было также щелкнуть курсором, например, ячейку E6 и затем командную строку вверху
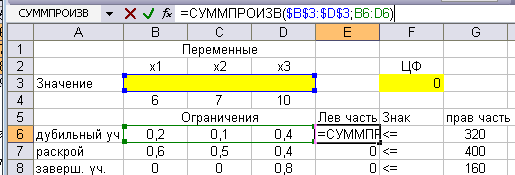
Аналогично проверим правильность набора формул в ячейках E7-E8.
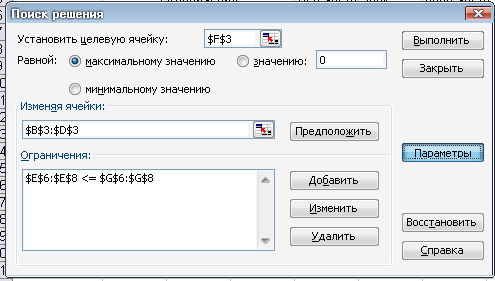
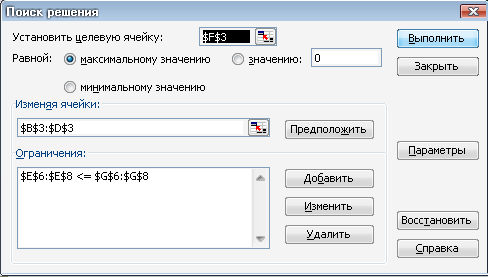
Теперь поставьте курсор в ячейку F3 целевой функции и на вкладкеДанные выберите Поиск решения.
Появится диалоговое окно:
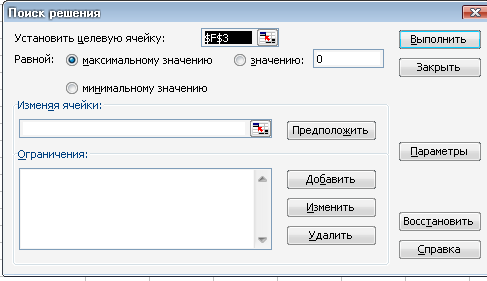
Отметить Максимальному значению
Щелкнуть курсором по полю Изменяемые ячейки и отметить курсором ячейки B3-D3:

Щелкнуть кнопку Добавить и в открывшемся окнеДобавление ограниченийв разделеСсылка на ячейкуотметить ячейкиE7 –E8:
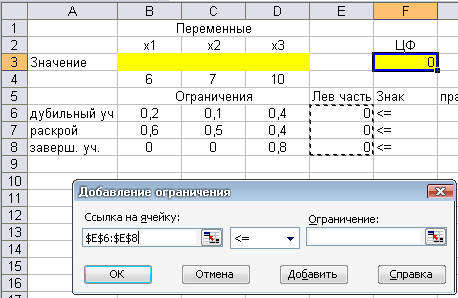
Поскольку автоматически установленное ограничение <= совпадает с нужным нам, то переходим к разделу Ограничение и в нем отмечаем ячейкиG6-G8:
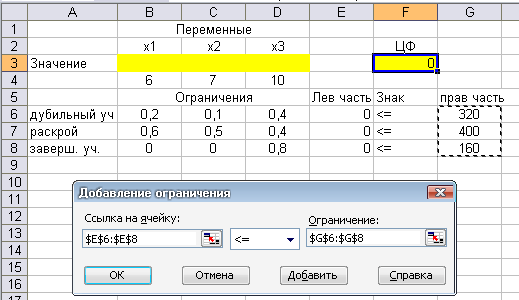
OK
Теперь нужно задать параметры поиска. Для этого в окне Поиск решениянажать кнопкуПараметры.
Появится окно Параметры поиска решения
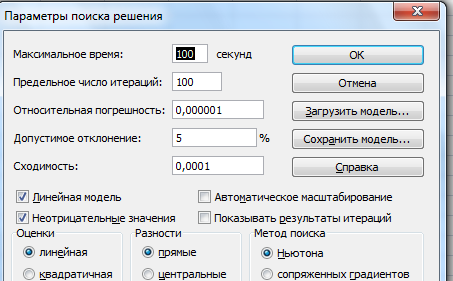
Установить Линейная модельиНеотрицательные значения(оценкилинейные, разностипрямые, метод поискаНьютона обычно установлены автоматически)
ОК.
В окне Поиск решениянажать кнопкуВыполнить
Появится окно Результаты поиска решения
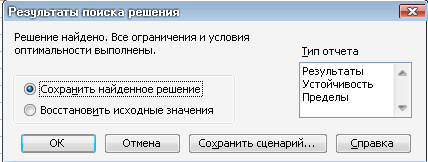
Если требуется провести экономический анализ полученного решения, то в окне Тип отчета указать, какой именно:
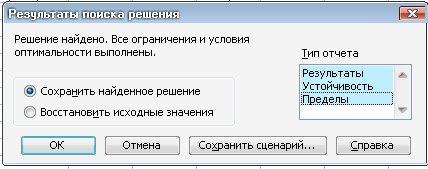
ОК.
Появится таблица с заполненными ячейками B3:D3, Е7:Е9 и максимальным значением целевой функции в ячейкеF3
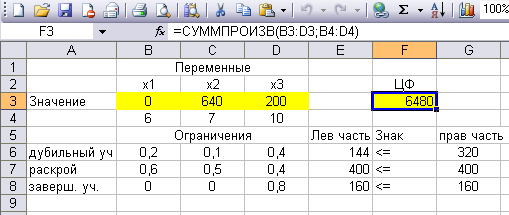
aтакже 3 новых листа: Отчёт по результатам 1, Отчёт по устойчивости 1, Отчет по пределам1.
Итак, максимальная прибыль – 6480 ден.ед. достигается при производстве 640 изделий вида В и 200 изделий вида С. Изделия А выпускать не рекомендуется.
Ресурс дубильного участка используется лишь в количестве 144 часов из 320 часов, т.е. наблюдается простой в работе дубильного участка в размере 320-144=176 часов.
Ресурсы времени раскройного и завершающего участков используются полностью, такие ресурсы называются связанными, илидефицитными.
В отчёте по результатамта же информация, что и в экранной форме:
|
Microsoft Excel 11.0 Отчет по результатам |
|
|
| |||
|
|
|
|
|
|
|
|
|
Целевая ячейка (Максимум) |
|
|
|
| ||
|
|
Ячейка |
Имя |
Исходное значение |
Результат |
|
|
|
|
$F$3 |
Значение ЦФ |
6480 |
6480 |
|
|
|
|
|
|
|
|
|
|
|
Изменяемые ячейки |
|
|
|
| ||
|
|
Ячейка |
Имя |
Исходное значение |
Результат |
|
|
|
|
$B$3 |
Значение x1 |
0 |
0 |
|
|
|
|
$C$3 |
Значение x2 |
640 |
640 |
|
|
|
|
$D$3 |
Значение x3 |
200 |
200 |
|
|
|
|
|
|
|
|
|
|
|
Ограничения |
|
|
|
| ||
|
|
Ячейка |
Имя |
Значение |
Формула |
Статус |
Разница |
|
|
$E$6 |
дубильный уч Лев часть |
144 |
$E$6<=$G$6 |
не связан. |
176 |
|
|
$E$7 |
раскрой Лев часть |
400 |
$E$7<=$G$7 |
связанное |
0 |
|
|
$E$8 |
заверш. уч. Лев часть |
160 |
$E$8<=$G$8 |
связанное |
0 |
Рассмотрим отчёт по устойчивости.
|
Microsoft Excel 11.0 Отчет по устойчивости |
|
|
|
| |||
|
Изменяемые ячейки |
|
|
|
|
| ||
|
|
|
|
Результ. |
Нормир. |
Целевой |
Допустимое |
Допустимое |
|
|
Ячейка |
Имя |
значение |
стоимость |
Коэффициент |
Увеличение |
Уменьшение |
|
|
$B$3 |
Значение x1 |
0 |
-2,4 |
6 |
2,4 |
1E+30 |
|
|
$C$3 |
Значение x2 |
640 |
0 |
7 |
5,5 |
2 |
|
|
$D$3 |
Значение x3 |
200 |
0 |
10 |
1E+30 |
4,4 |
|
|
|
|
|
|
|
|
|
|
Ограничения |
|
|
|
|
| ||
|
|
|
|
Результ. |
Теневая |
Ограничение |
Допустимое |
Допустимое |
|
|
Ячейка |
Имя |
значение |
Цена |
Правая часть |
Увеличение |
Уменьшение |
|
|
$E$6 |
дубильный уч Лев часть |
144 |
0 |
320 |
1E+30 |
176 |
|
|
$E$7 |
раскрой Лев часть |
400 |
14 |
400 |
880 |
320 |
|
|
$E$8 |
заверш. уч. Лев часть |
160 |
5,5 |
160 |
440 |
160 |
Нормированная стоимостьизделия – это величина убытков фирмы при принудительном выпуске одного изделия, выпускать которое не рекомендуется. В данном случае при принудительном выпуске одного изделия А убытки составят 2,4 ден. ед.
|
Microsoft Excel 11.0 Отчет по устойчивости |
| ||||
|
|
|
|
| ||
|
Изменяемые ячейки |
|
|
| ||
|
|
|
Результ. |
Нормир. | ||
|
Ячейка |
Имя |
значение |
стоимость | ||
|
$B$3 |
Значение x1 |
0 |
-2,4 | ||
|
$C$3 |
Значение x2 |
640 |
0 | ||
|
$D$3 |
Значение x3 |
200 |
0 | ||
Допустимое увеличение или уменьшение коэффициентов целевой функции.
Последние два столбца дают информацию о возможных колебаниях коэффициентов целевой функции (в данном случае – прибыли от продажи изделий), не влияющих на оптимальный план (т.е. при таких колебаниях прибыли разработанный план производства изменять не надо).
|
Microsoft Excel 11.0 Отчет по устойчивости |
|
|
|
| |||
|
|
|
|
|
|
|
|
|
|
Изменяемые ячейки |
|
|
|
|
| ||
|
|
|
|
Результ. |
Нормир. |
Целевой |
Допустимое |
Допустимое |
|
|
Ячейка |
Имя |
значение |
стоимость |
Коэффициент |
Увеличение |
Уменьшение |
|
|
$B$3 |
Значение x1 |
0 |
-2,4 |
6 |
2,4 |
1E+30 |
|
|
$C$3 |
Значение x2 |
640 |
0 |
7 |
5,5 |
2 |
|
|
$D$3 |
Значение x3 |
200 |
0 |
10 |
1E+30 |
4,4 |
Итак, выработанный оптимальный план
производства не изменится, если прибыль
от продажи изделия А будет дальше как
угодно уменьшаться или же увеличится
не более чем на 2,4 ден. ед., т.е. до размера
8,4 ден. ед. Если же прибыль от продажи
изделия А увеличится более, чем не 2,4
ден. ед., т.е. станет больше 8,4 ден. ед, то
производство изделий А станет выгодным,
и для определения оптимального плана
производства нужно заново решать
задачу.![]()
Оптимальный план производства не изменится, если прибыль от продажи изделия В уменьшится не более, чем на 2 ден. ед. или увеличится не более, чем на 5,5 ден .ед, т.е. будет находиться в пределах [5: 12,5].
При этом прибыль
![]()
будет колебаться от значения
![]() ден .ед,
ден .ед,
до значения
![]() ден .ед,
ден .ед,
Оптимальный план производства не изменится, если прибыль от продажи изделия С уменьшится не более, чем на 4,4 ден. ед., увеличение возможно любое.
При этом прибыль будет увеличиваться от значения
![]() ден .ед,
ден .ед,
неограниченно.
Теневая ценахарактеризует ценность дефицитного ресурса, она показывает увеличение прибыли от каждой дополнительной единицы ресурса. Так, в данной задаче теневая цена для раскройного участка 14 ден. ед. – это величина прибыли от каждой дополнительного часа работы этого участка. Каждый дополнительный час работы завершающего участка даст дополнительную прибыль 5,5 ден. ед., таким образом, при появлении свободных средств их в первую очередь нужно направлять на расширение раскройного участка.
|
|
|
|
|
|
|
Ограничения |
|
| ||
|
|
|
|
Результ. |
Теневая |
|
|
Ячейка |
Имя |
значение |
Цена |
|
|
$E$6 |
дубильный уч Лев часть |
144 |
0 |
|
|
$E$7 |
раскрой Лев часть |
400 |
14 |
|
|
$E$8 |
заверш. уч. Лев часть |
160 |
5,5 |
Кроме того, в двух последних столбцах отчета указано допустимое увеличение и уменьшение запасов ресурсов, которое не повлияет на оптимальный план производства.
|
Ограничения |
|
|
|
|
| ||
|
|
|
|
Результ. |
Теневая |
Ограничение |
Допустимое |
Допустимое |
|
|
Ячейка |
Имя |
значение |
Цена |
Правая часть |
Увеличение |
Уменьшение |
|
|
$E$6 |
дубильный уч Лев часть |
144 |
0 |
320 |
1E+30 |
176 |
|
|
$E$7 |
раскрой Лев часть |
400 |
14 |
400 |
880 |
320 |
|
|
$E$8 |
заверш. уч. Лев часть |
160 |
5,5 |
160 |
440 |
160 |
В данной задаче рассчитанный оптимальный план остается в силе если:
мощность дубильного участка будет наращиваться неограниченно, поскольку время его работы и сейчас имеется в избытке, уменьшить время работы дубильного участка можно на 176 часов;
время работы раскройного участка увеличить на 880 часов или сократить на 320 часов;
время работы завершающего участка увеличить на 440 часов или сократить на 160 часов.
Экономический анализ графического решения ЗЛП
Определить оптимальный план производства,
если изделий, если , калькуляция, запасы
ресурсов и прибыль от реализации изделий
заданы таблицей: при условии, что изделий
А нужно выпустить 5 штук.
![]() Решить
задачу графически, провести экономический
анализ и анализ решения на чувствительность.
Решить
задачу графически, провести экономический
анализ и анализ решения на чувствительность.
|
Ресурсы ( ч ) |
Потребление ресурсов на единицу продукции |
Ограничения на ресурсы ( ч ) | ||
|
А 5 |
В |
С | ||
|
Дубильный участок |
1 |
1 |
1 |
45 |
|
Раскройный участок |
1 |
3 |
1 |
65 |
|
Завершающий участок |
0 |
0 |
5 |
165 |
|
Прибыль (ден.ед.) |
6 |
3 |
2 |
|
Пусть выпускается ![]() штук изделий вида B
иCсоответственно.
Тогда прибыль от продажи всех изделий
штук изделий вида B
иCсоответственно.
Тогда прибыль от продажи всех изделий
![]() ,
и
,
и
![]()
Ограничения по запасам ресурсов:
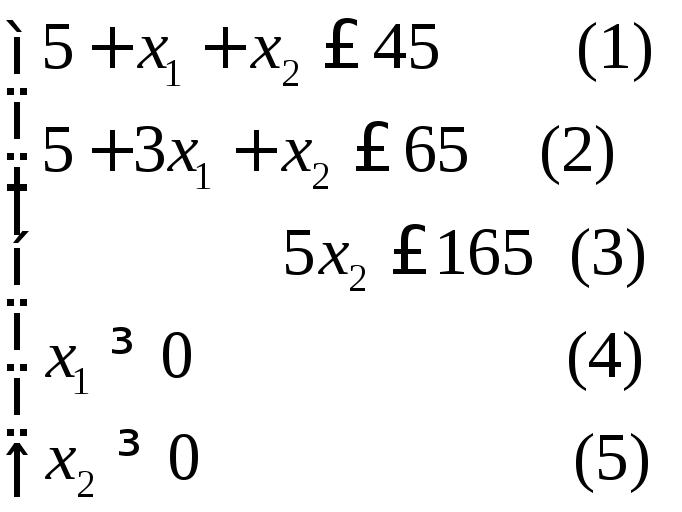
Графическое решение задачи
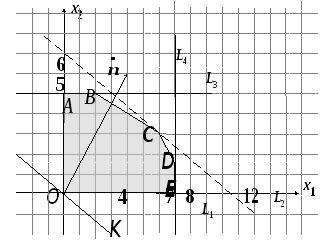
Построим область допустимых решений. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами.
Построим границы области:
![]() или
или![]()
|
|
0 |
40 |
|
|
40 |
0 |
Выбрав точку (0; 0), определим знак
неравенства в полуплоскости: 1 • 0 + 1 •
0 ≤40 - верно, т.е.
неравенство![]() задает часть плоскости, расположенную
ниже прямой
задает часть плоскости, расположенную
ниже прямой![]() .
.
![]() (2) или
(2) или![]()
![]()
|
|
0 |
20 |
|
|
60 |
0 |
Выбрав точку (0; 0), определим знак
неравенства в полуплоскости: 3 • 0 + 2 •
0 ≤60 - верно, т.е.
неравенство![]() задает часть плоскости, расположенную
ниже прямой
задает часть плоскости, расположенную
ниже прямой![]() .
.
![]() 165 (3)
165 (3)![]()
![]()
Эта прямая проходит через точку x2= 165/5 = 33 параллельно оси OX. Определим
полуплоскость, задаваемую неравенством.
Выбрав точку (0; 0), определим знак
неравенства в полуплоскости: 5 • 0≤165 - верно, т.е. неравенство 5x2≤
165 задает часть плоскости, расположенную
ниже прямой![]() .
.
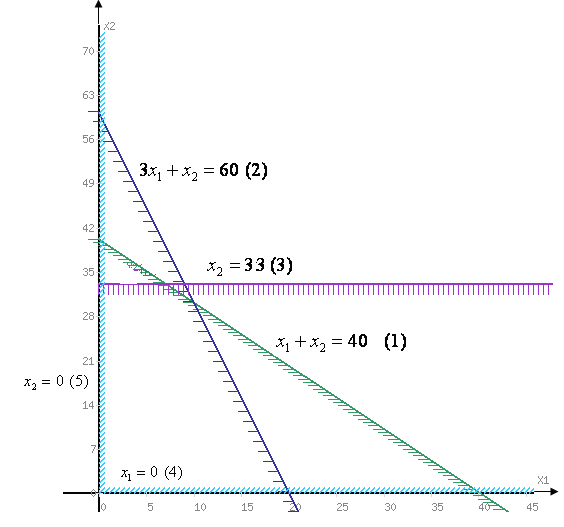
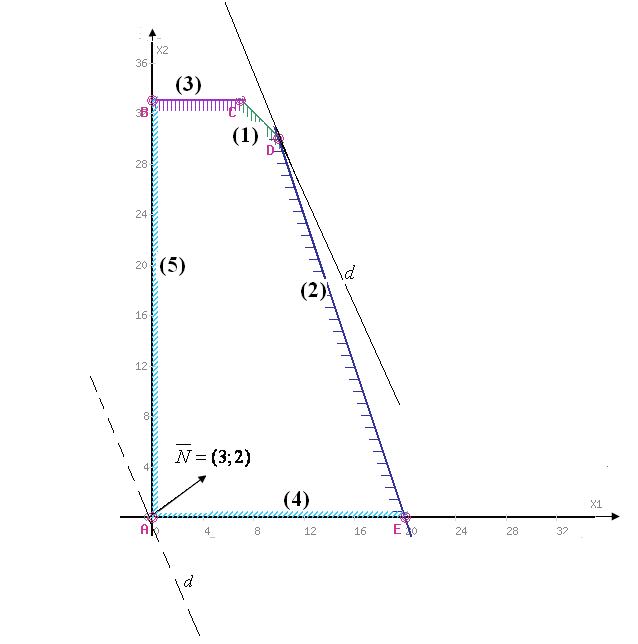
Итак, область допустимых решений имеет вид:
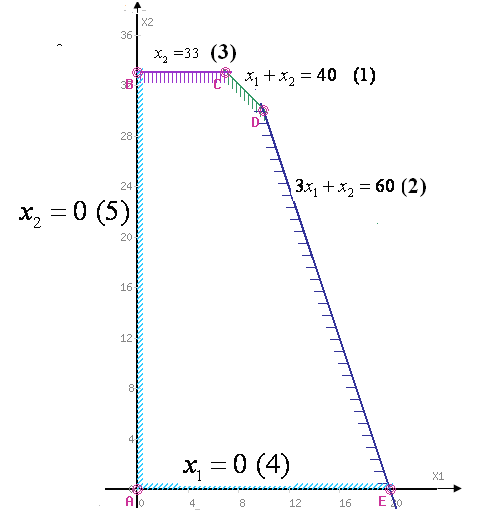
Вектор-градиент
![]() ,
составленный из коэффициентов целевой
функции, указывает направление
максимизации F(X). Прямая
,
составленный из коэффициентов целевой
функции, указывает направление
максимизации F(X). Прямая![]() - начальный опорный план. Будем двигать
эту прямую параллельно в направлении
вектора
- начальный опорный план. Будем двигать
эту прямую параллельно в направлении
вектора![]() .
Поскольку нас интересует максимальное
решение, то двигаем прямую
.
Поскольку нас интересует максимальное
решение, то двигаем прямую![]() до последнего касания области. На графике
это точка
до последнего касания области. На графике
это точка![]() .
.
Так как точка D получена в результате
пересечения прямых (1)и(2), то ее
координаты удовлетворяют уравнениям
этих прямых: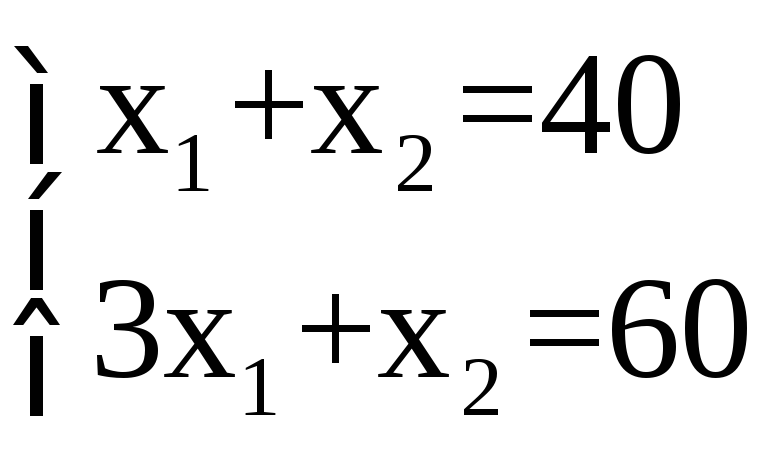 Решив
систему уравнений, получим: x1=
10, x2= 30. Найдем максимальное
значение целевой функции:
Решив
систему уравнений, получим: x1=
10, x2= 30. Найдем максимальное
значение целевой функции:
![]() .
.
Итак, максимальная прибыль 120 ден. ед. достигается при выпуске 10 изделий В 30 изделий С.
Экономический анализ результатов решения.
Подставив
![]() координаты
оптимального решения
координаты
оптимального решения
![]() в каждое неравенство системы ограничений
в каждое неравенство системы ограничений
 ,
,
видим, что первое и второе неравенства обращаются в уравнения, а третье– в строгое неравенство
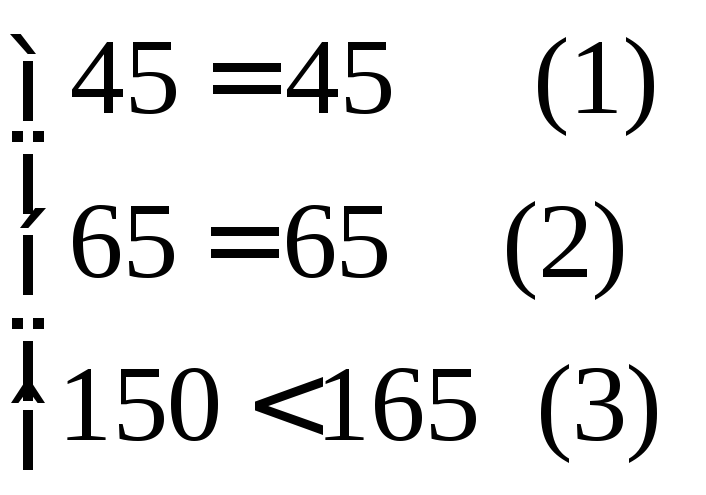 ,
,
что означает, что время работы дубильного и раскройного участков используется полностью и является дефицитным ресурсом, а время работы завершающего участка присутствует в избытке, максимальное его потребление составляет 150 часов, излишек составляет
165-150=15 часов.
Анализ решения задачи на чувствительность.
Анализ решения задачи на чувствительность предполагает ответ на следующие вопросы:
на сколько можно увеличить запасы дефицитных ресурсов;
какова ценность дополнительной единицы каждого дефицитного ресурса;
на сколько можно уменьшить запасы недефицитных ресурсов;
В каких пределах могут колебаться коэффициенты целевой функции
при неизменности оптимального решения.
Увеличение запаса дефицитных ресурсов
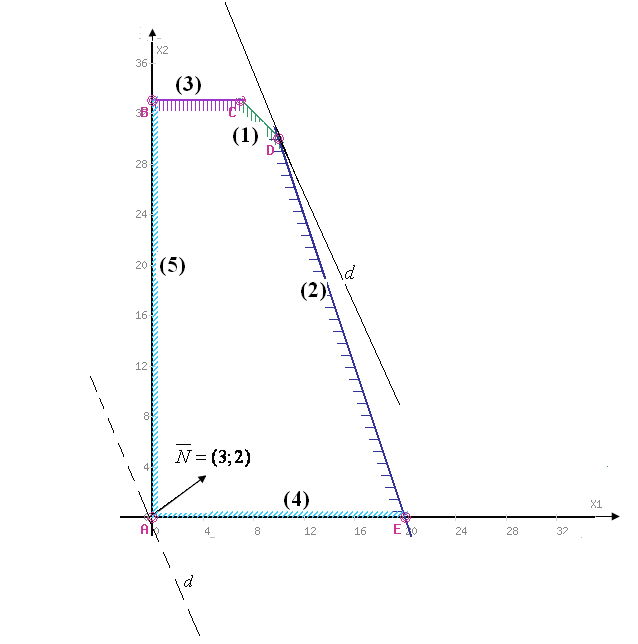
Исследуем, насколько можно увеличить мощности дефицитных ресурсов - время работы дубильного раскройного участков.
Из рисунка видно, что при увеличении времени работы дубильного участка прямая (1) перемещается вверх параллельно самой себе, постепенно "стягивая" в точку треугольник CGD.
В точке G ограничение (1) для сырья I становится избыточным, ограничения (2) и (3) становятся активными, пространством (допустимых) решений становится многоугольник ABGE
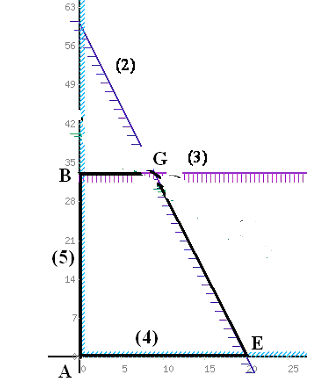
.
оптимальному решению при этом будет соответствовать точка G:

Координаты точки G, в которой пересекаются прямые (2) и (3):
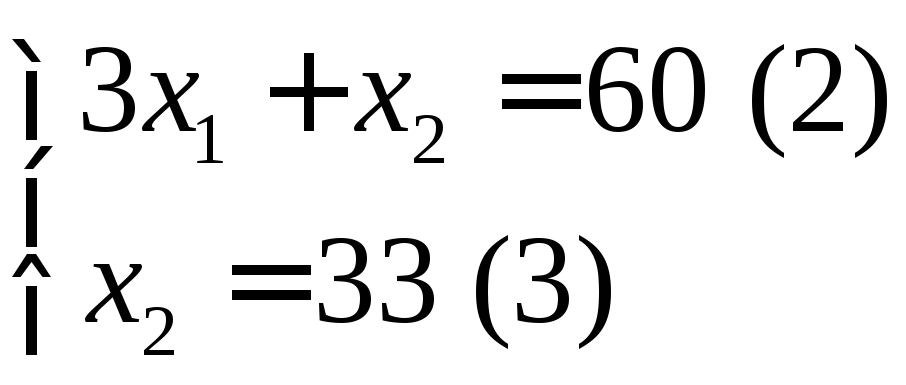
![]()
Подставим
координаты точки
![]() в левую часть ограничения
в левую часть ограничения
![]()
и определим максимальное разумное увеличение времени работы дубильного участка:
![]() ч.
ч.
Следовательно, время работы дубильного участка можно увеличивать с 45 до 47 ч. При этом F достигнет значения:
![]() ден. ед.
ден. ед.
Из рисунка видно, что при увеличении времени работы раскройного участка прямая (2) перемещается вправо параллельно самой себе, доходя до точки К, стягивая в точку треугольник КDE.
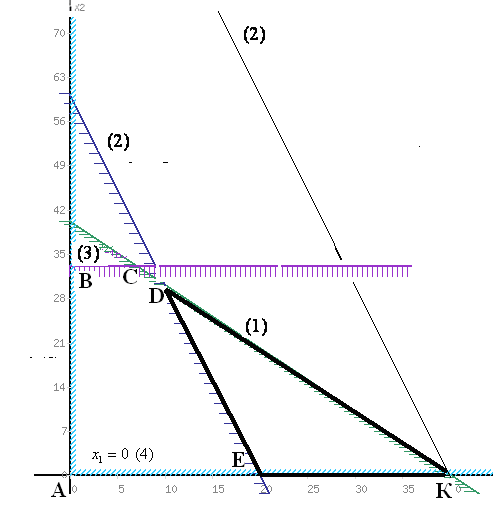
Пространством допустимых решений становится многоугольник ABCK,.
В точке К ограничение (2) для сырья II становится избыточным, активными становятся ограничения (4) и (1)

оптимальному решению при этом будет соответствовать точка К(40; 0),
Подставим
координаты точки К(40; 0) в левую часть
ограничения
![]() (2) и определим максимальное разумное
увеличение времени работы раскройного
участка:
(2) и определим максимальное разумное
увеличение времени работы раскройного
участка:
![]() ч.
ч.
Следовательно, время работы
раскройного участка можно увеличивать
с 65 до125,![]()
при этом
![]()
Уменьшение запасов недефицитных ресурсов
Исследуем, на сколько можно уменьшить запас недефицитного ресурса (убрать излишки), в данной задаче это время работы завершающего участка.
Правую часть ограничения можно уменьшать
до тех пор, пока прямая
![]() не достигнет точки
не достигнет точки
![]() .
.
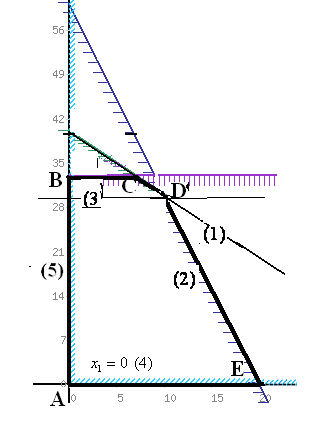
При этом правая часть ограничения (3)
станет равной
![]() ,
значит,время работы завершающего
участка можно снизить со 165 до 150 часов.
,
значит,время работы завершающего
участка можно снизить со 165 до 150 часов.
Определение ценности дополнительной единицы дефицитного ресурса
Результаты анализа сведем в таблицу:
|
Ограничение |
Тип ресурса |
Максимальное
изменение запаса ресурса
|
Максимальное изменение ЦФ
|
|
Ограничение по времени работы дубильного участка |
Дефицитный |
47-45=2 ч
|
|
|
Ограничение по времени работы раскройного участка |
Дефицитный |
125-65=60 ч
|
|
|
ограничение по времени работы завершающего участка |
Недефицитный |
165-150=15 ч |
|
Ценность дополнительной единицы ресурса
![]() (теневая цена):
(теневая цена):
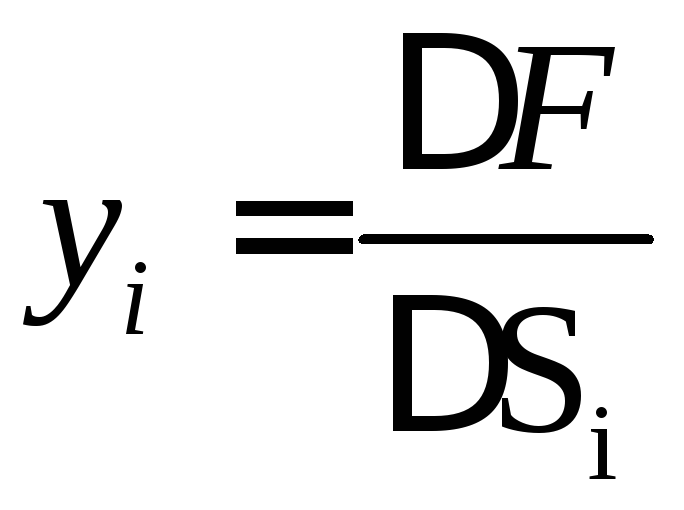
Ценность каждого дополнительного часа работыдубильного участка:
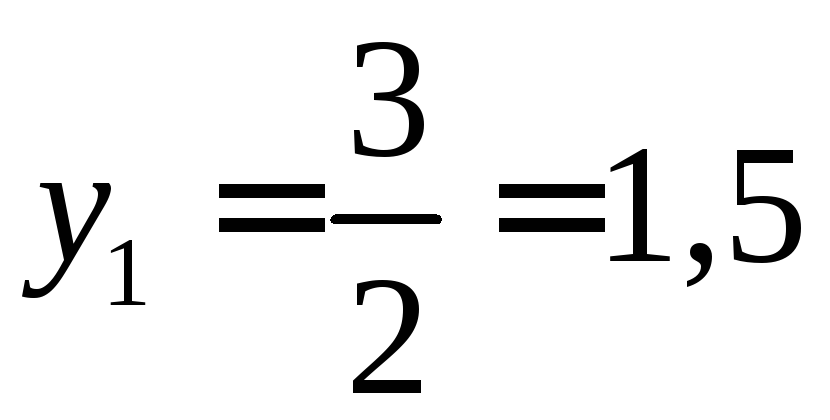 -
-
Т.е. каждый дополнительный час работы дубильного участка принесет дополнительную прибыль 1,5 ден. ед.
Ценность каждого дополнительного часа работыраскройного участка:
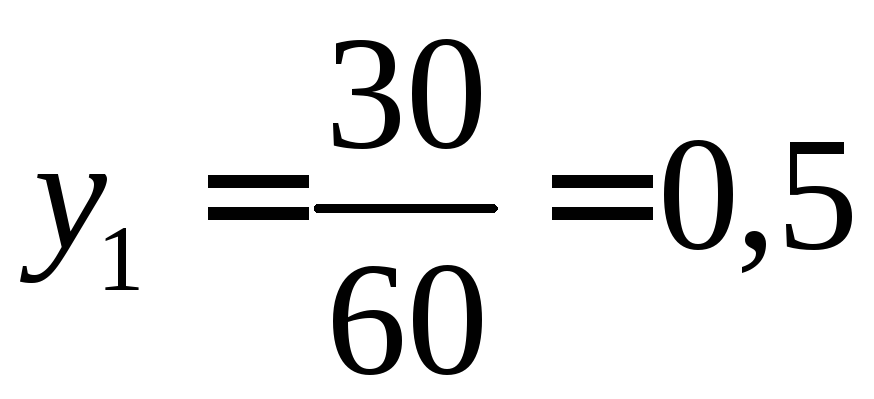 -
-
Т.е. каждый дополнительный час работы раскройного участка принесет дополнительную прибыль 0,5 ден. ед.
Таким образом, дополнительные вложения в первую очередь следует направить на расширение дубильного участка и лишь затем - на расширение закройного участка.
Анализ изменения коэффициентов целевой функции

Обозначим через
![]() и
и![]() доходы от продажи одной единицы изделия
B и одной единицы изделия Г соответственно.
Тогда:
доходы от продажи одной единицы изделия
B и одной единицы изделия Г соответственно.
Тогда:
![]() .
.
Напомним, что угловым
![]() коэффициентом прямой
коэффициентом прямой![]() является коэффициент при
является коэффициент при![]() в уравнении прямой с угловым коэффициентом
(это уравнение, в котором выражена
переменнаяy), т.е.
в уравнении прямой с угловым коэффициентом
(это уравнение, в котором выражена
переменнаяy), т.е.
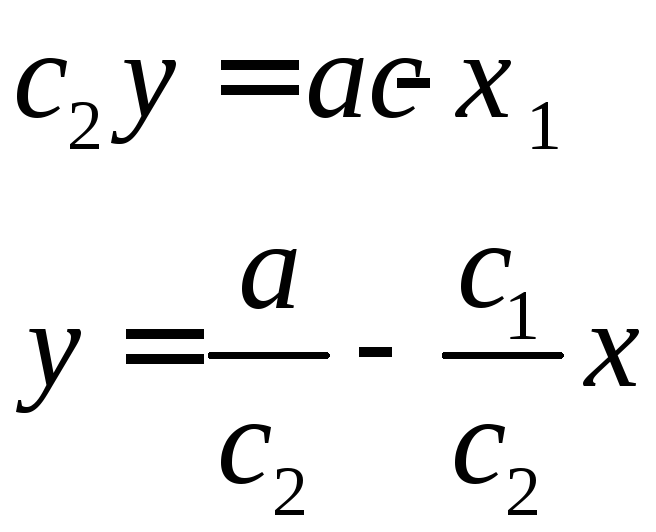
![]() =
=![]() .
.
Угловой коэффициент равен тангенсу угла наклона данной прямой к положительному направлению оси OX.
Если выразить переменную
![]() ,
то коэффициент при
,
то коэффициент при![]() есть тангенс угла наклона прямой к
положительному направлению осиOY.
есть тангенс угла наклона прямой к
положительному направлению осиOY.
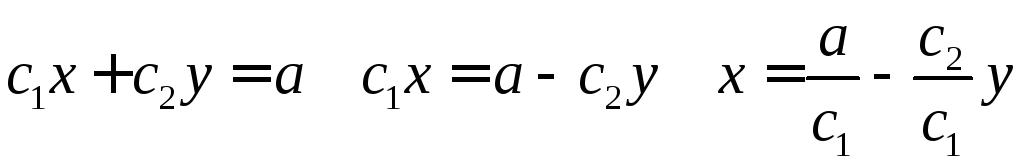
![]() =
=![]()
Целевая функция имеет вид
![]()
Если
![]() (линия уровня С), то уравнение
(линия уровня С), то уравнение
![]() -
-
задает семейство параллельных прямых,
![]() или
или![]()
при
![]()
![]()
Поскольку прямые параллельны, то все
они имеют один и тот же угловой
коэффициент, и находить его можно для
любой прямой из этого семейства, например,
для прямой, у которой
![]() (этому соответствует положение прямой
(этому соответствует положение прямой![]() ,
проходящей через начало координат):
,
проходящей через начало координат):
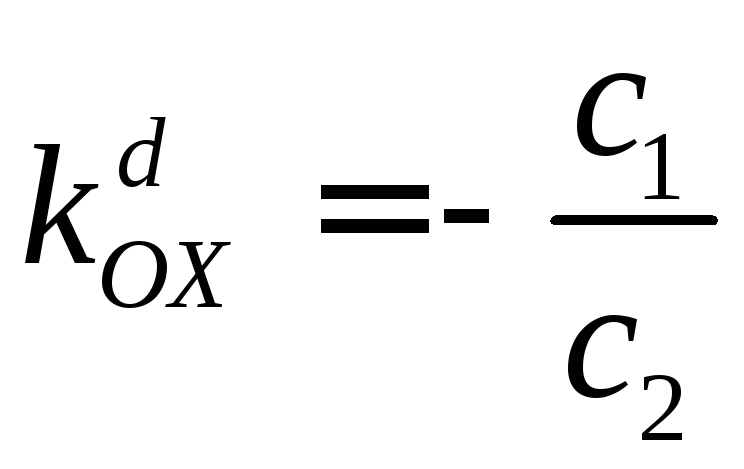

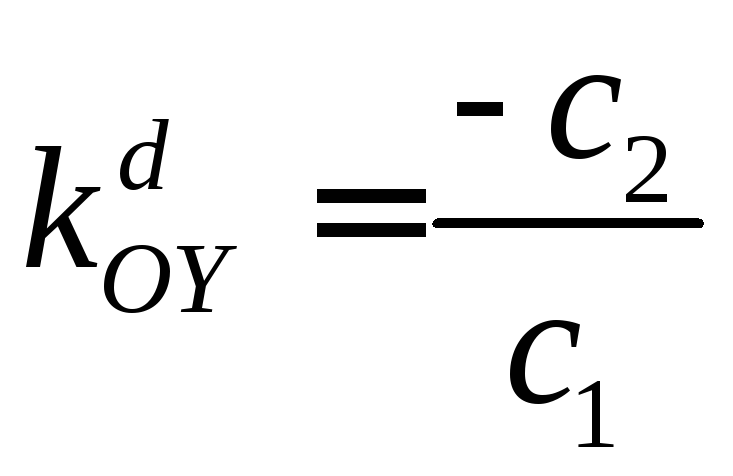
Переместим линию уровня
![]() в точку максимумаD.
в точку максимумаD.
При уменьшении ее углового коэффициента прямая dсовместится с граничной линией (2), а при увеличении ее углового коэффициента – с граничной линией (1).
Точка Dбудет оставаться
оптимальной точкой до тех пор, пока угол
наклона линии![]() к
осиOXбудет лежать между
углами наклона этих прямых, т.е.
к
осиOXбудет лежать между
углами наклона этих прямых, т.е.
![]()
![]()
![]()
![]()
![]()
и, значит,
![]()
![]()
![]()
![]()
![]()
Найдем
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Для линии (1):
![]()
![]() =
- 1
=
- 1
![]()
![]() =-1
=-1
Для линии (2)
![]()
![]()
![]() =
- 3
=
- 3
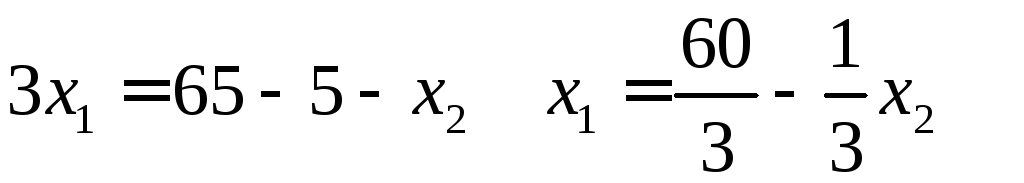
![]() =
=![]()
Поскольку
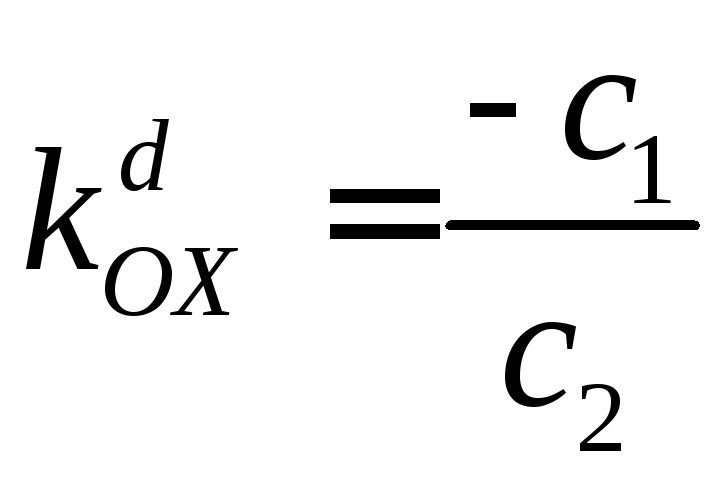 ,
,![]() =
- 3,
=
- 3,![]() =
- 1, то
=
- 1, то
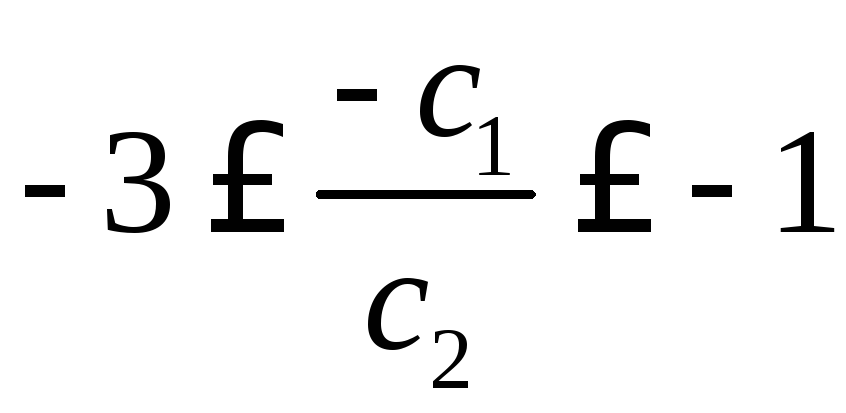
![]()
![]()
При условии, что прибыль
![]() от
продажи единицы изделия остается на
прежнем уровне
от
продажи единицы изделия остается на
прежнем уровне![]() ,
имеем:
,
имеем:
![]()
![]() ,
,
т.е. при неизменной прибыли от изделия Г прибыль от изделия В может колебаться от 2 до 6 ден.ед., что не повлечет изменения оптимального решения.
Точка Dбудет оставаться
оптимальной точкой и до тех пор, пока
угол наклона линии![]() к
осиOYбудет лежать между
углами наклона этих прямых, т.е.
к
осиOYбудет лежать между
углами наклона этих прямых, т.е.
![]()
![]()
![]()
![]()
![]() ,
,
А поскольку
![]() =-1,
=-1,![]() =
=![]() ,
,![]() =
=![]() ,
то
,
то
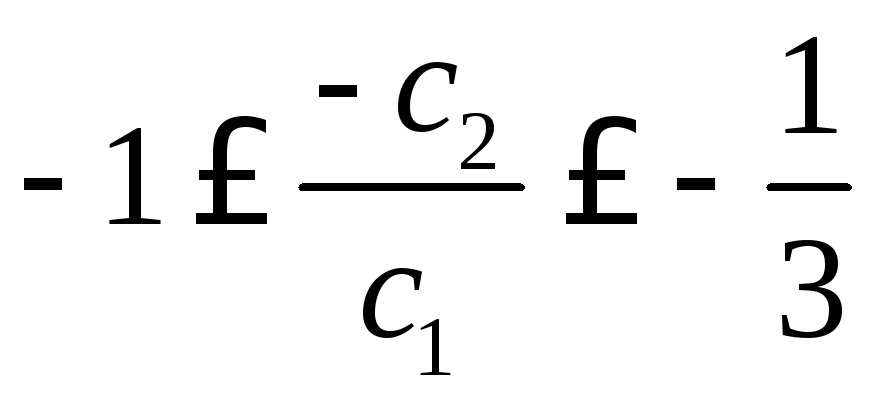
![]()
![]() .
.
При условии, что прибыль
![]() от
продажи единицы изделия остается на
прежнем уровне
от
продажи единицы изделия остается на
прежнем уровне![]() ,
имеем:
,
имеем:
![]()
![]() ,
,
т.е. при неизменной прибыли от изделия В прибыль от изделия Г может колебаться от 1 до 3 ден.ед., что не повлечет изменения оптимального решения.
А что будет, если угловой коэффициент
(наклон к оси OX) опорной
прямой![]() станет меньше углового коэффициента
прямой (2)? В этом случае точкой максимума
функции
станет меньше углового коэффициента
прямой (2)? В этом случае точкой максимума
функции![]() станет точкаE(40;0), т.е.
производить изделия Г станет невыгодно,
потребление первого ресурса (времени
работы дубильного участка) сократится
и он перестанет быть дефицитным.
Дефицитным останется второй ресурс –
время работы раскройного участка.
станет точкаE(40;0), т.е.
производить изделия Г станет невыгодно,
потребление первого ресурса (времени
работы дубильного участка) сократится
и он перестанет быть дефицитным.
Дефицитным останется второй ресурс –
время работы раскройного участка.
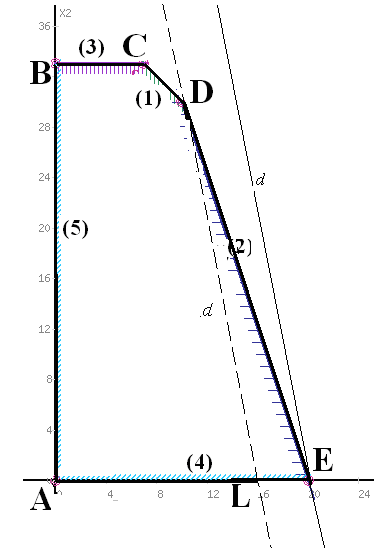
Если угловой коэффициент (наклон к оси
OX) опорной прямой![]() станет больше углового коэффициента
прямой (1),
станет больше углового коэффициента
прямой (1),
то точкой максимума функции
![]() станет точка С, в которой пересекаются
прямые
станет точка С, в которой пересекаются
прямые
![]() и
и![]() 165 (3), т.е.
165 (3), т.е.
![]() С(7;33),
С(7;33),
дефицитными ресурсами станут третий и первый – время работы дубильного и завершающего участка, а время работы раскройного участка сократится и перестанет быть дефицитным.
Взаимно двойственные задачи линейного программирования

Рассмотрим пару задач линейного программирования, связанных между собой симметричными зависимостями:
в задаче (1) требуется минимизировать целевую функцию:
 ,
а в задаче (2) - максимизировать:
,
а в задаче (2) - максимизировать: ;
;все ограничения задачи (1) – неравенства вида
 ,
все ограничения задачи (2) – неравенства
–вида
,
все ограничения задачи (2) – неравенства
–вида ;
;в задаче (1) nнеизвестных иmограничений (без учета условий неотрицательности), в задаче (2)mнеизвестных иnограничений (без учета условий неотрицательности);
матрицы из коэффициентов при переменных
 ,
,
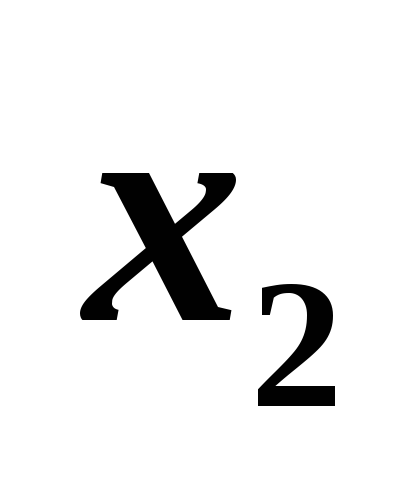 ,…,
,…, задач (1) и при переменных
задач (1) и при переменных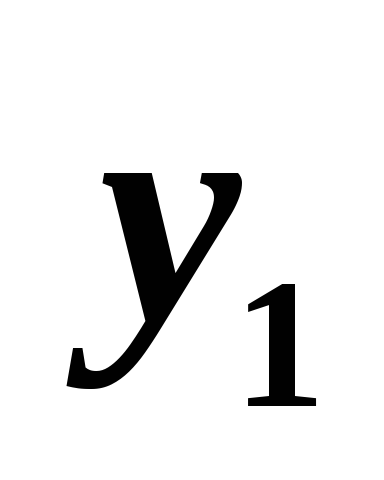 ,
,
 ,…,
,…,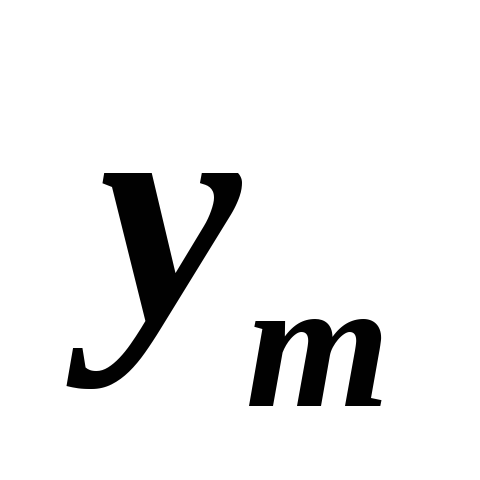 задачи (2) являются взаимно
транспонированными;
задачи (2) являются взаимно
транспонированными;правые части системы ограничений задачи (1) – это коэффициенты целевой функции задачи (2); коэффициенты целевой функции задачи (1) – это правые части системы ограничений задачи (2);
каждому ограничению задачи (1) в виде неравенства соответствует условие неотрицательности ассоциированной с этим ограничением переменной задачи; каждому ограничению задачи (1) в виде равенства соответствует переменная задачи (2) без ограничений на знак
каждому ограничению задачи (2) в виде неравенства соответствует неотрицательная переменная задачи (1), каждому ограничению задачи (2) в виде равенства соответствует переменная задачи (1) произвольного знака.
Такие задачи называют парой двойственных задачлинейного программирования (или простодвойственной парой).
-
Задача 1
Задача 2
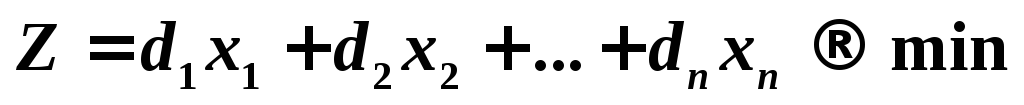
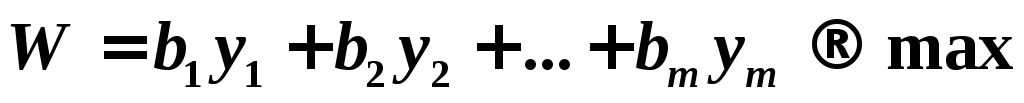
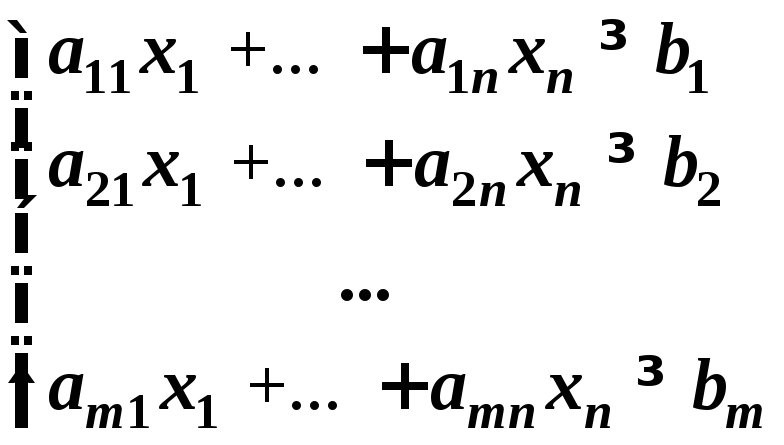
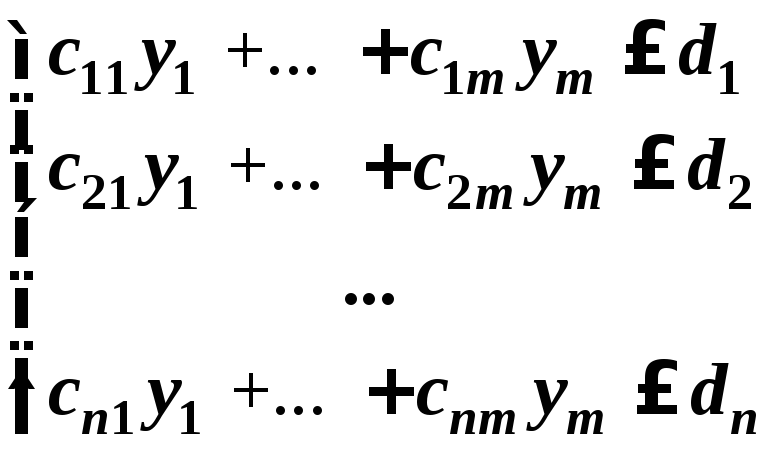
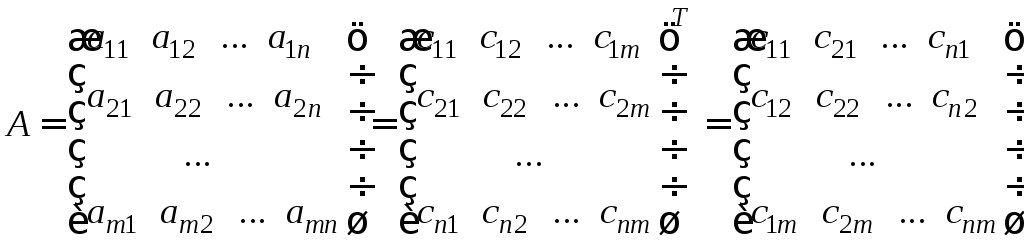
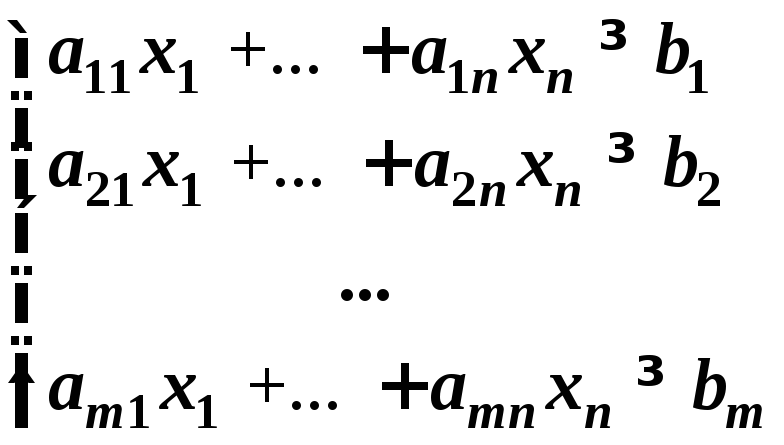
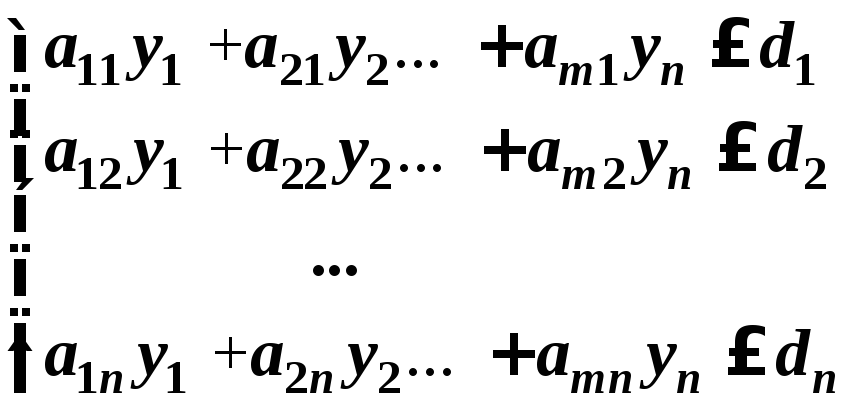
Пример 1. Построить задачу, двойственную следующей задаче линейного программирования:
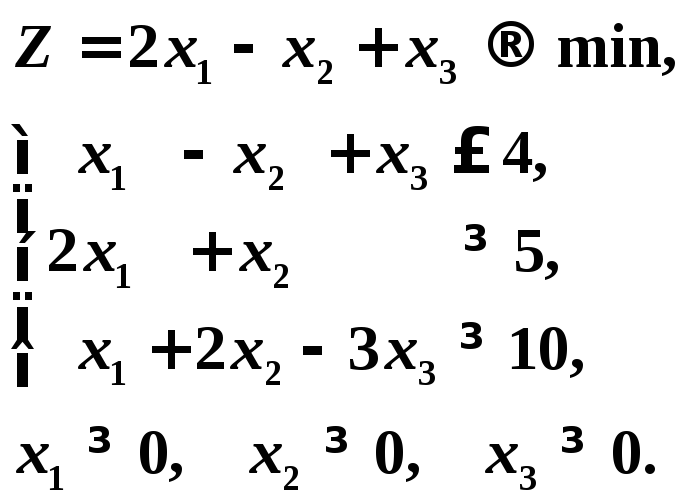


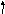 δ4
δ4




 1
1