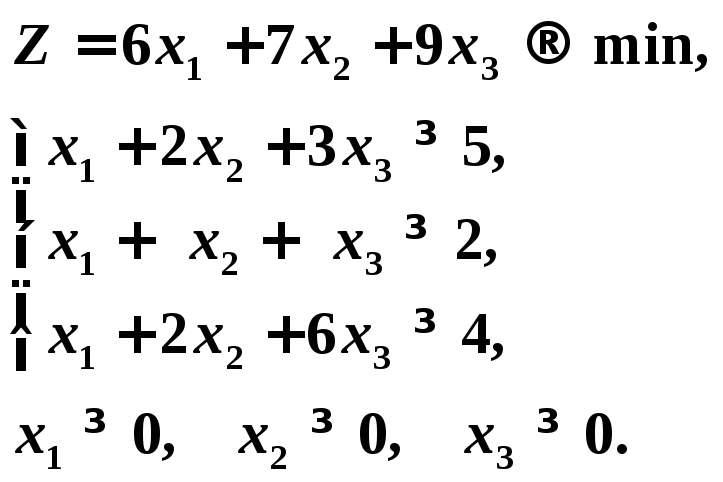Решение

Умножим первое ограничение – неравенство на -1. Задача примет вид задачи (2) симметричной пары двойственных задач:

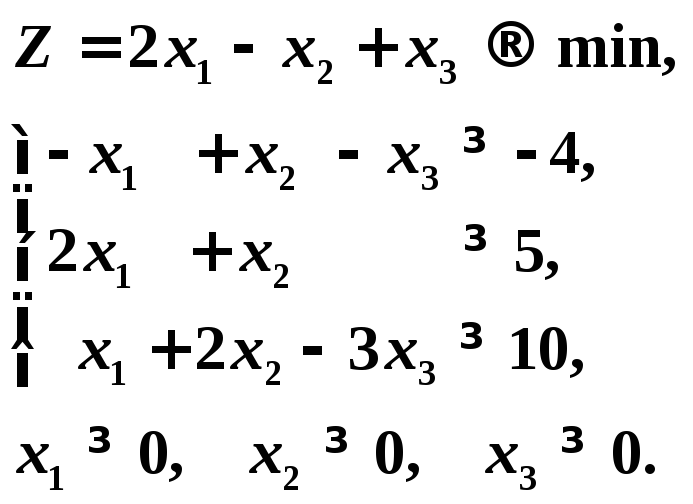
Умножим правые части ограничений на соответствующие переменные двойственной задачи и сложим их, получим целевую функцию.

.

Функция максимизируется, так как целевая функция исходной задачи минимизируется.

Умножаем коэффициенты при на соответствующие переменные двойственной задачи и складываем их:

.

Данная сумма меньше или равна коэффициенту при в целевой функции:

.

Неравенство имеет вид «», потому что целевая функция двойственной задачи максимизируется. Аналогично составляются еще два ограничения двойственной задачи (соответствуют переменным, ):

Все переменные двойственной задачи удовлетворяют неотрицательности, потому что все ограничения исходной задачи – неравенства.

Окончательно двойственная задача имеет вид:

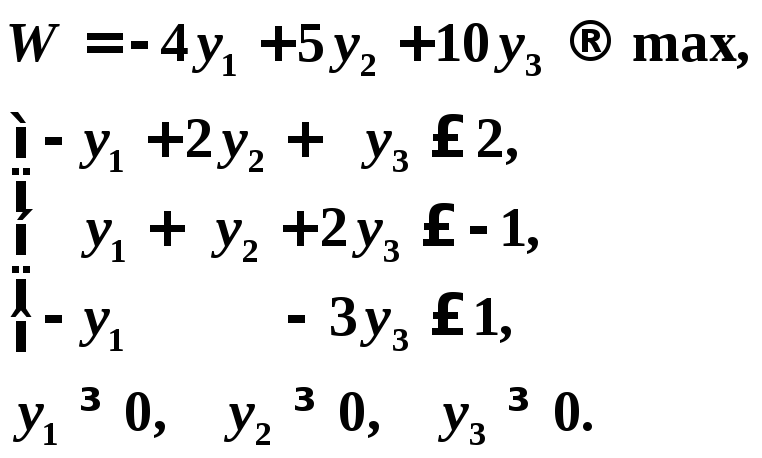
Пример 2. Построить задачу, двойственную данной задаче линейного программирования:

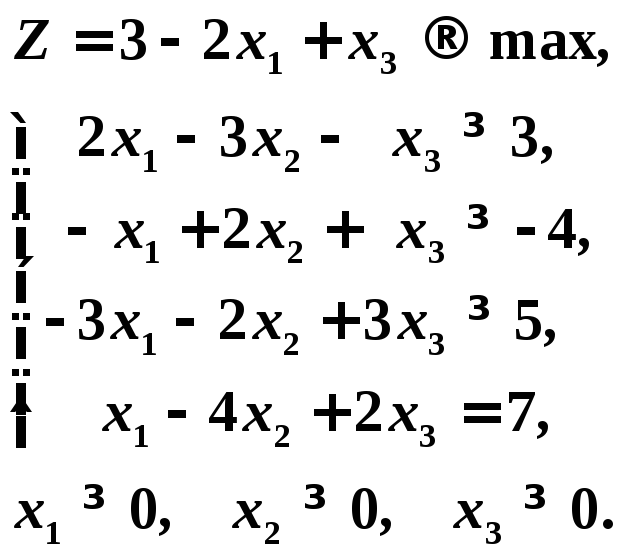
Решение

Будем использовать условия, которым должны удовлетворять двойственные задачи. Умножим ограничения – неравенства на (-1), так как в задаче на максимум они должны иметь вид «». Исходная задача запишется в виде:

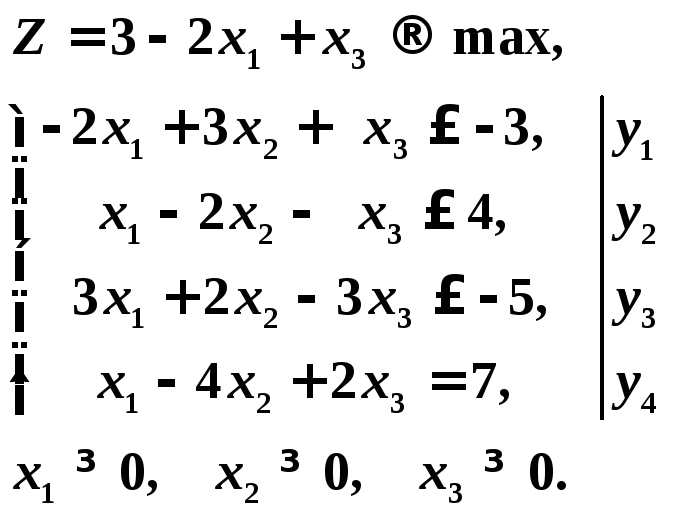
Составим двойственную задачу:

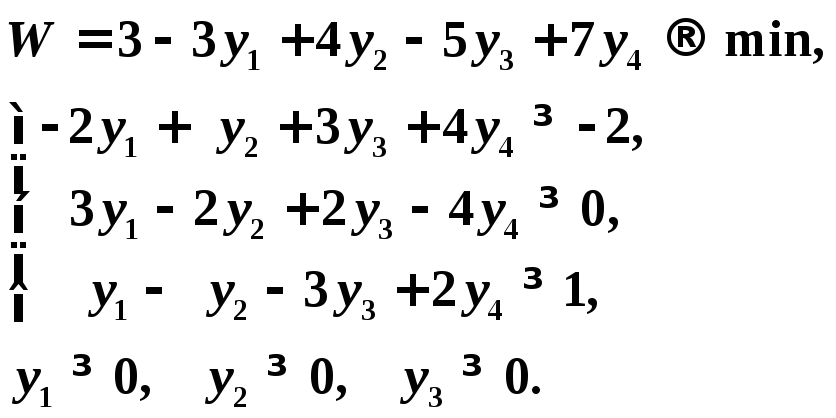
Переменная , соответствующая ограничению равенства, может быть любого знака.

В теории двойственности есть теоремы, которые позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач. Решив одну из пары двойственных задач, можно или найти оптимальное решение другой задачи, не решая ее, или установить его отсутствие.

Теорема 1.Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная к ней имеет оптимальное решение, причем значения целевых функций задач на своих оптимальных решениях совпадают. Если же одна из пары двойственных задач не имеет решения ввидунеограниченности целевой функции, то другая не имеет решения ввидунесовместности системы ограничений.

Теорема 2. Для того, чтобы допустимые решения,являлись оптимальными решениями пары двойственных задач, необходимо и достаточно, чтобы выполнялись следующие равенства:

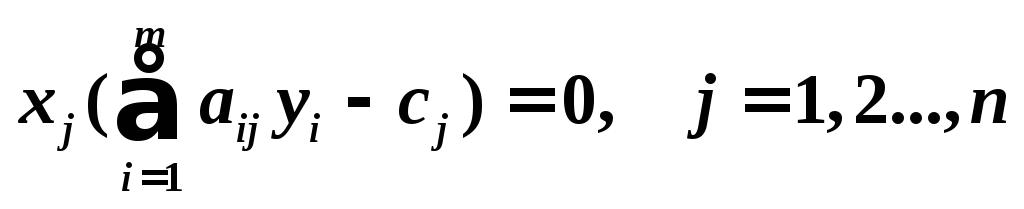(1)

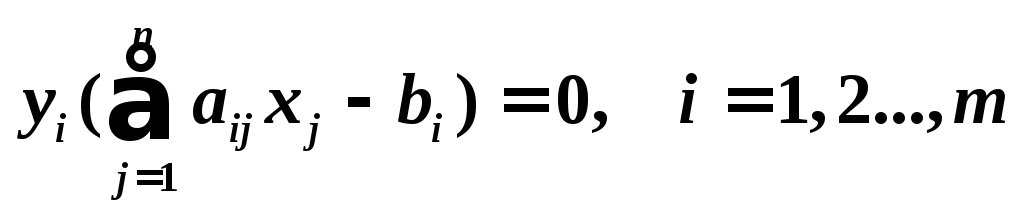(2)

Иначе, если при подстановке оптимального решения в систему ограничений i-е ограничение исходнойзадачи выполняетсякак строгое неравенство,то i-я координатаоптимального решениядвойственнойзадачи равна нулю,

и, наоборот, если i-я координатаоптимального решениядвойственной задачи отлична от нуля, то i-е ограничение исходной задачиудовлетворяется оптимальным решениемкак равенство.

Задача 1	Задача 2
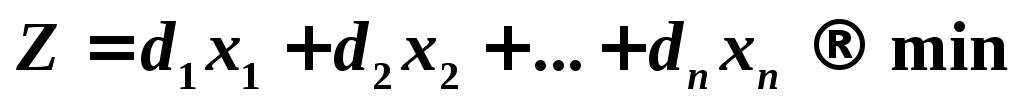
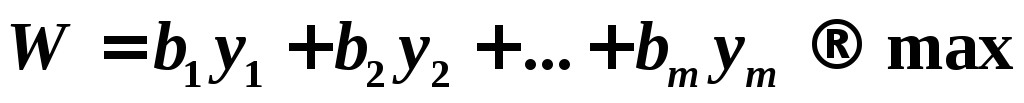
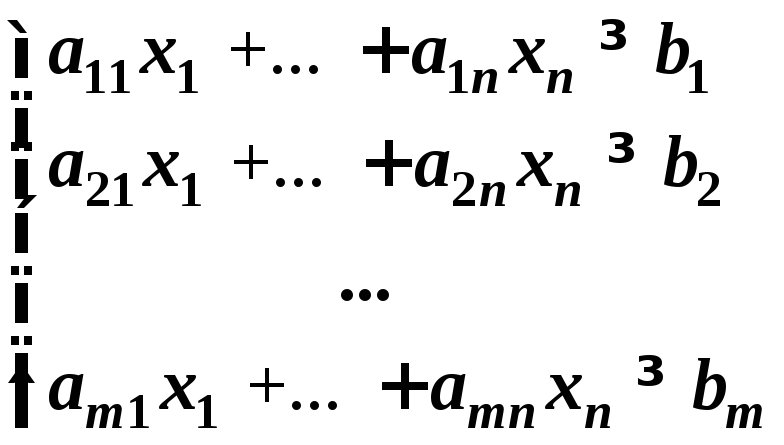
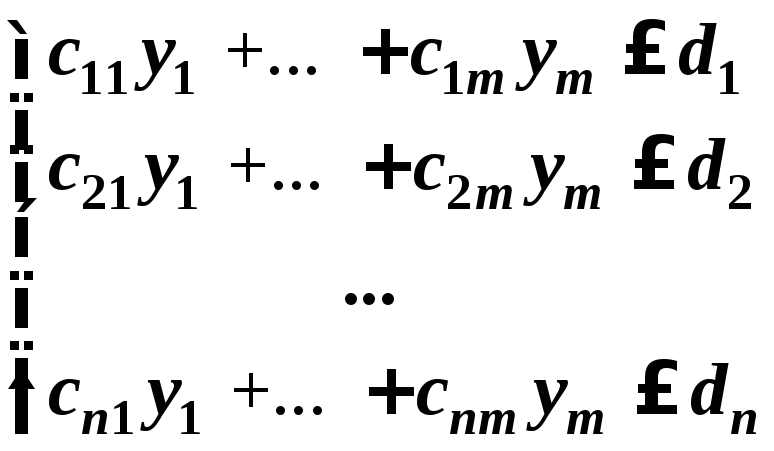
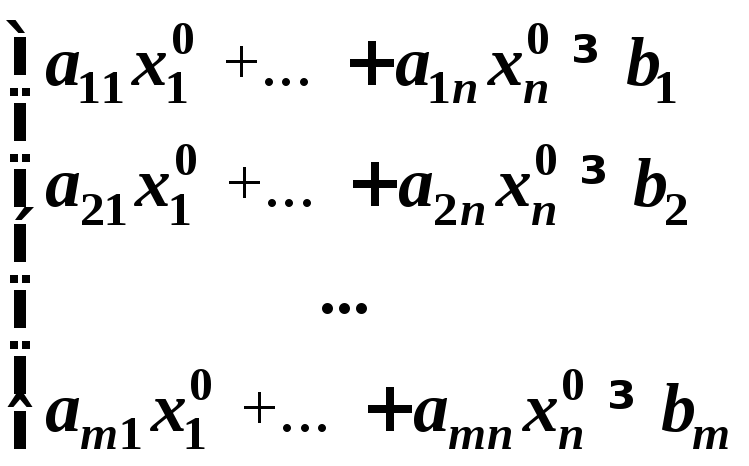
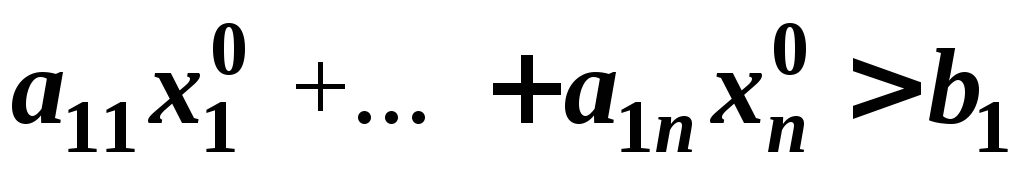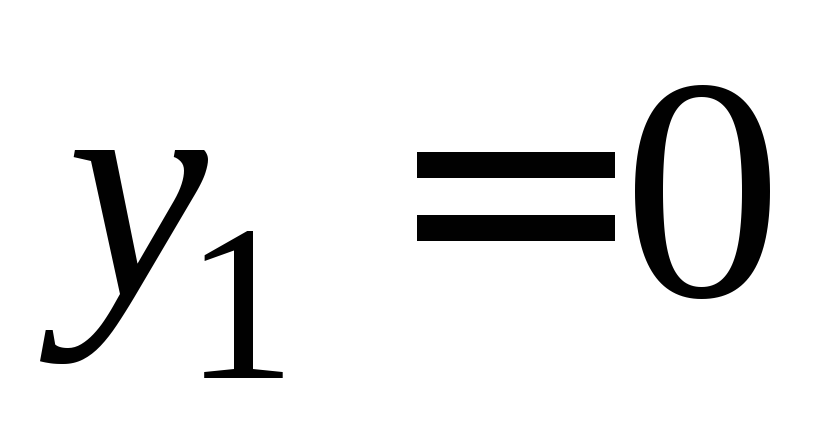
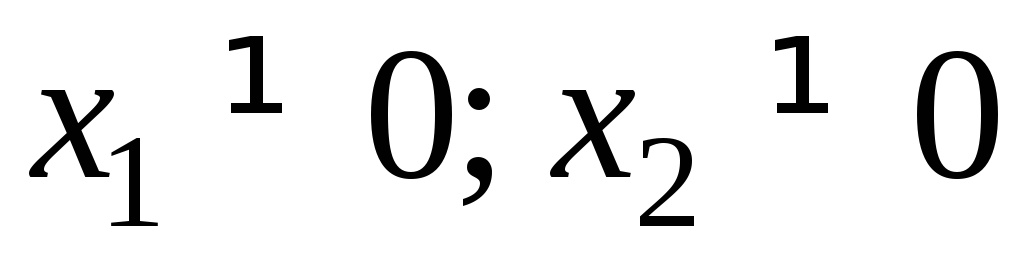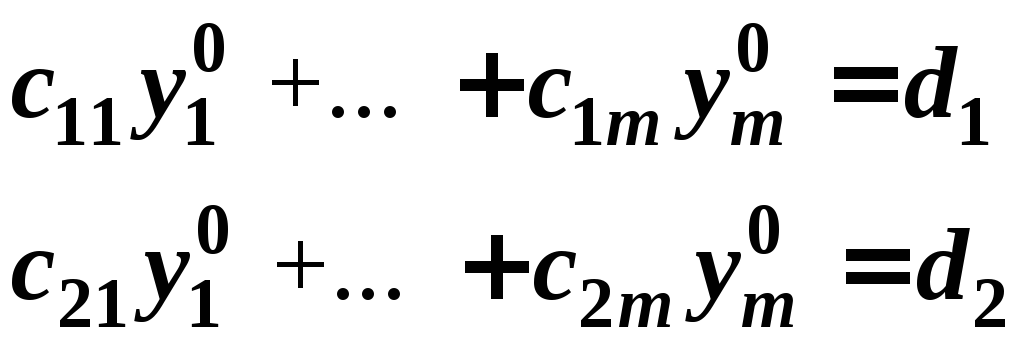
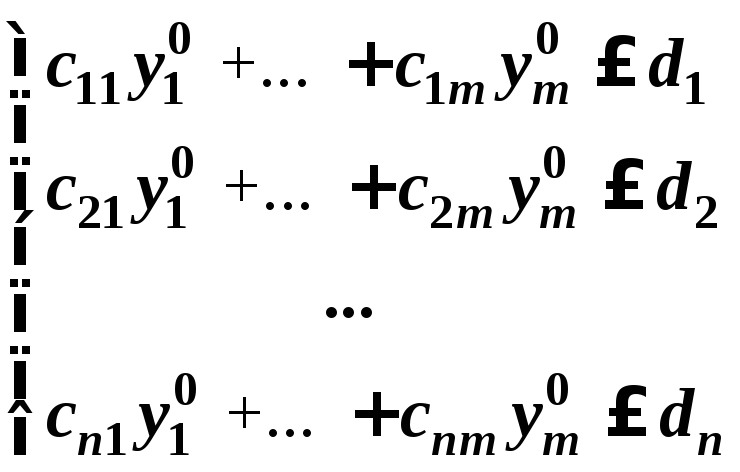
Подставим оптимальное решение в систему ограничений Пусть, например, , тогда Если, например, , то	Подставим оптимальное решение в систему ограничений Пусть, например, 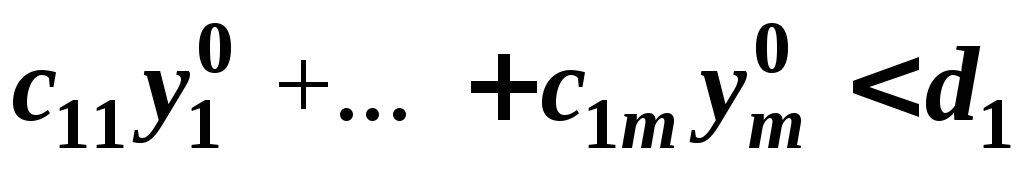, тогда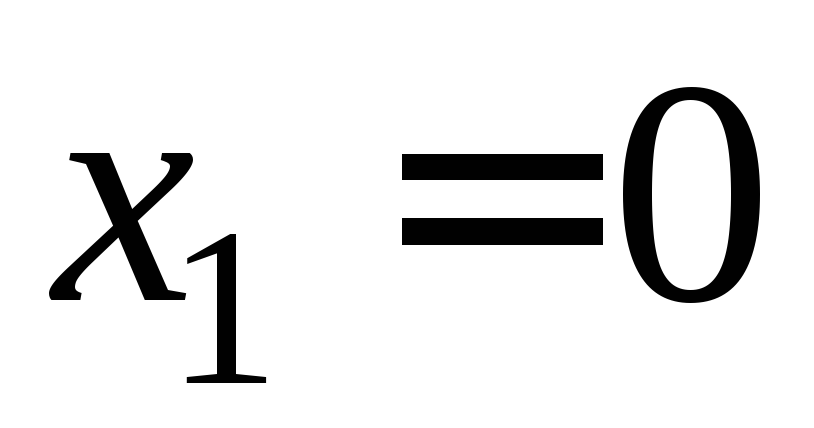 Если, например, 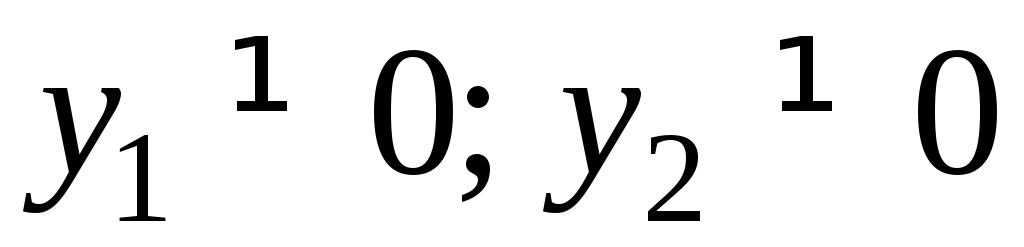, то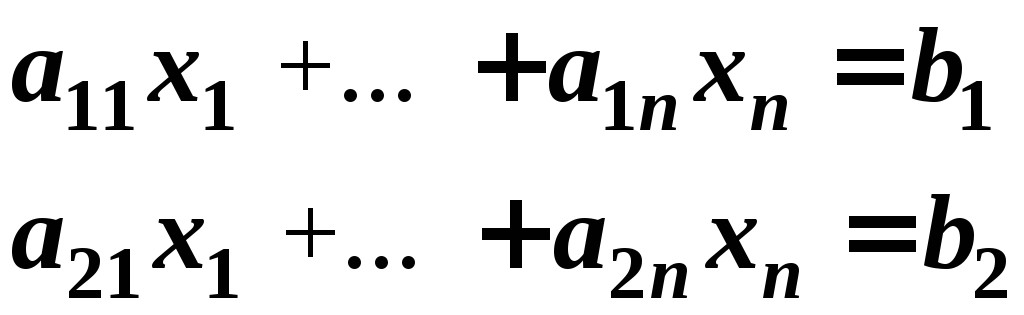

Пример 3. Для данной задачи составить двойственную, решив ее графическим методом и, используя вторую теорему, найти решение исходной задачи:

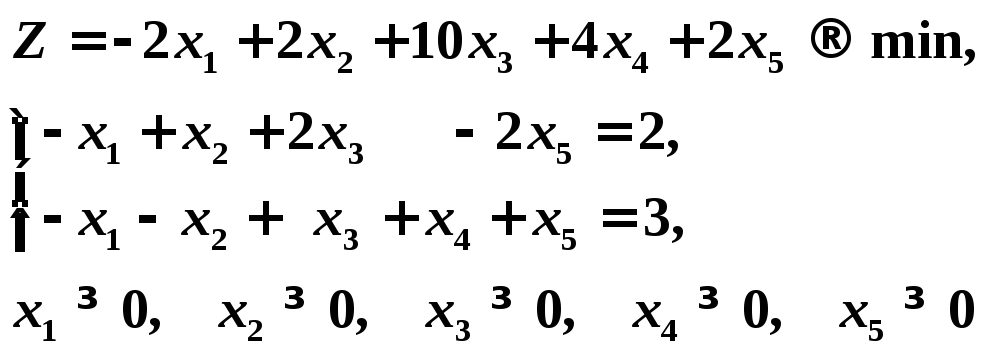
Решение

1. Составим двойственную задачу, запишем ограничения:

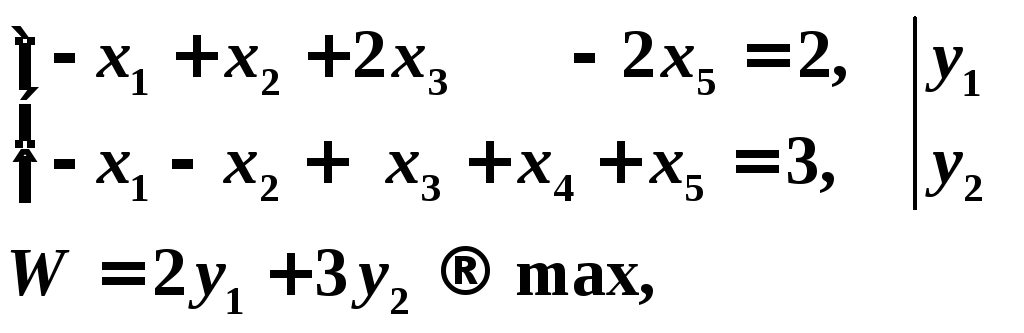
2. Решим полученную задачу графически. Для этого изобразим область допустимых решений

Уравнения границ области:

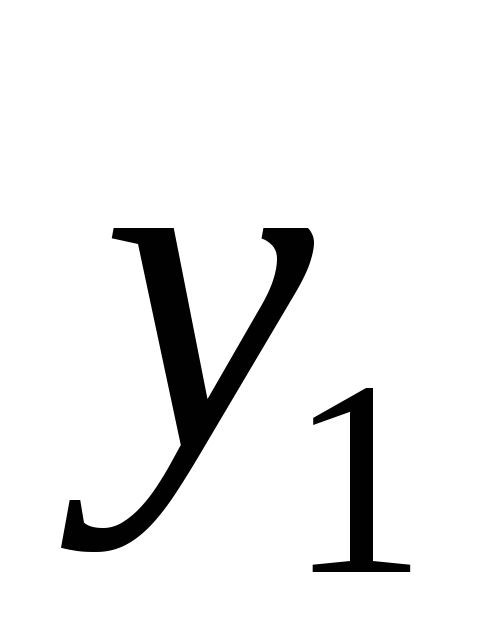
	0	2
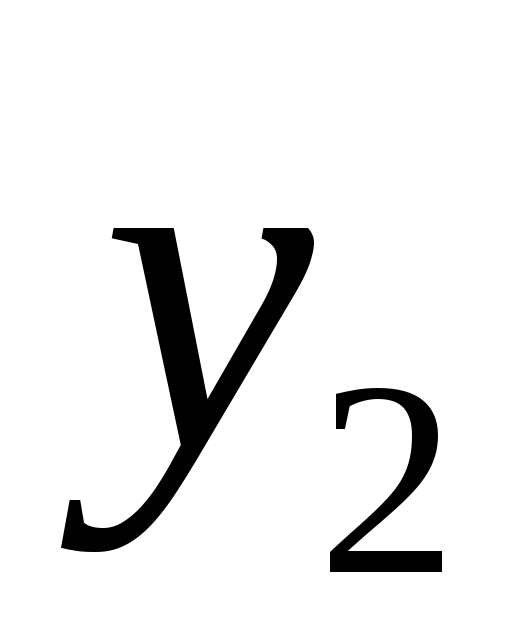
	2	0

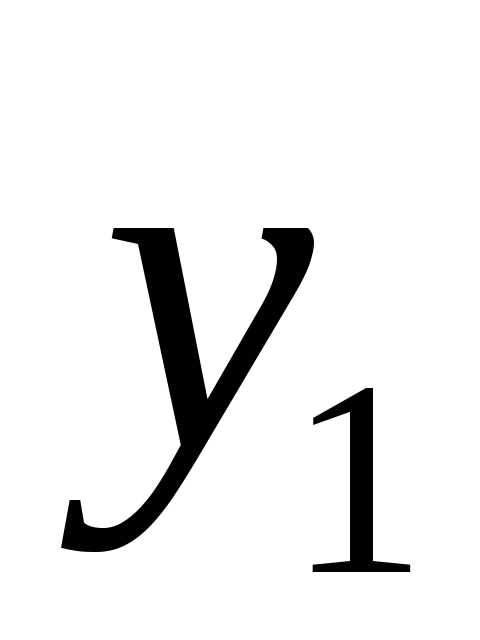
	0	2
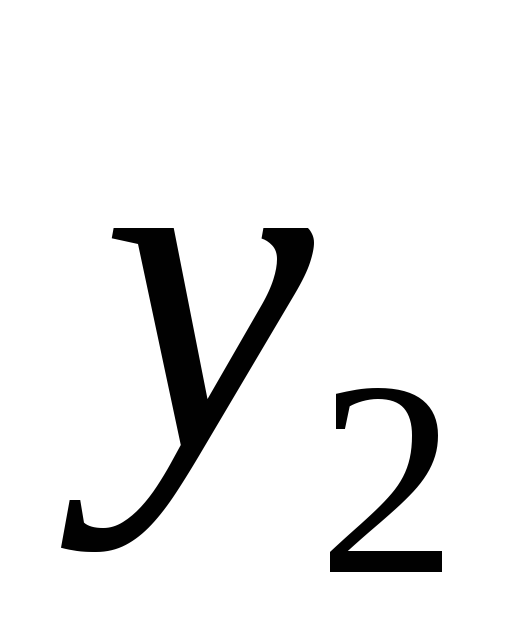
	-2	0

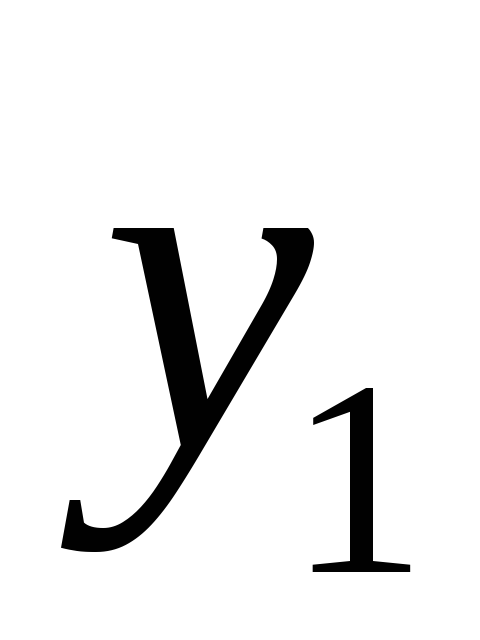
	0	5
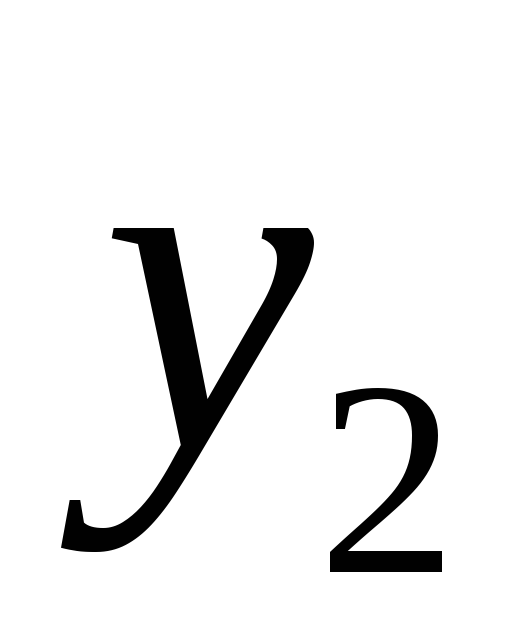
	10	0

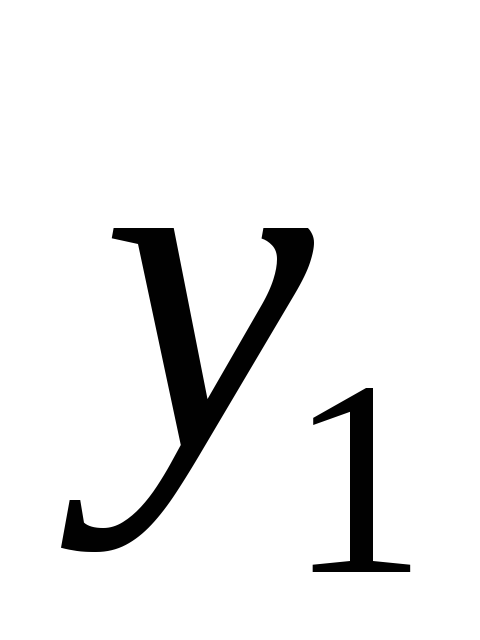
	0	-1
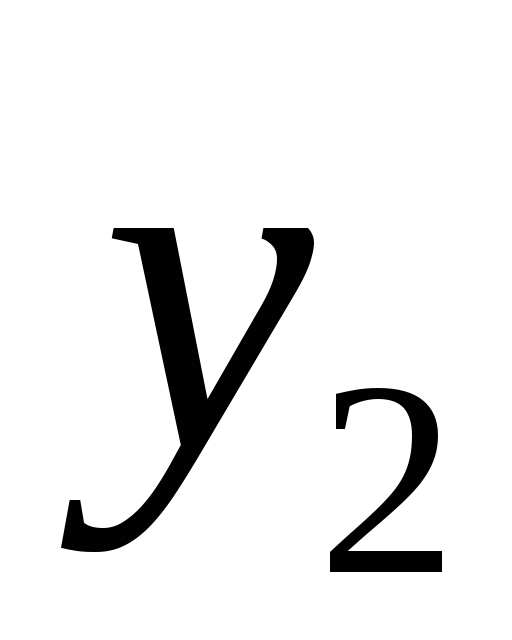
	2	0

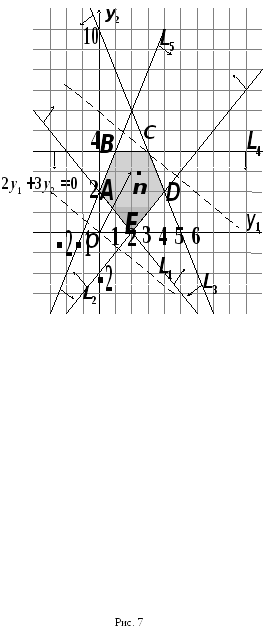
Область допустимых решений полученной задачи – многоугольник ABCDЕ.

Для линий уровня строим вектор нормали. Перпендикулярно векторупостроим одну из линий уровня, например,.

Так как задача на максимум, то перемещаем линию уровня в направлении вектора до опорной прямой. В данном случае опорной прямой является прямая, проходящая через точкуСпересечения прямыхи, то есть:

Следовательно, оптимальное решение:

3. Подставим оптимальное решение в систему ограничений. Получим, что, первое, второе и пятое ограничения выполняются как строгие неравенства.

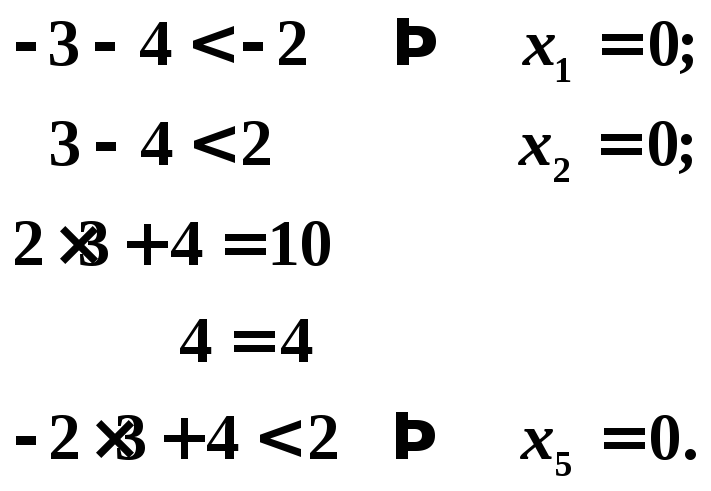
По теореме 2 следует, что соответствующие координаты оптимального решения исходной задачи (двойственной задачи), равны нулю .

Учитывая это, из системы ограничений исходной задачи получим:

Оптимальное решение исходной задачи:

.

Ответ:

Пример 4. Для данной задачи составить двойственную, решить ее симплексным методом и, используя теорему 2, найти решение исходной задачи.