
- •Глава I. Теоретические и методические аспекты изучения линий второго порядка
- •Глава II. Практическое применение икт при изучении линий второго порядка
- •Глава I. Теоретические и методические аспекты изучения линий второго порядка Пункт 1. Теория линий второго порядка и использования икт в обучении
- •Понятие линии второго порядка в аналитической геометрии
- •Приведение общего уравнения линии второго порядка к каноническому виду
- •Линии второго порядка в элементарной математике
- •Вывод уравнения окружности
- •Исследование свойств окружности по её уравнению
- •2) Симметрия окружности:
- •Изображение окружности
- •Вывод уравнения эллипса
- •Исследование свойств эллипса по его уравнению
- •1) Пересечение эллипса с осями координат:
- •2) Симметрия эллипса относительно координатных осей ox и oy:
- •Вывод уравнения гиперболы
- •Исследование свойств гиперболы по ее уравнению
- •1) Пересечение гиперболы с осями координат:
- •2) Симметрии гиперболы относительно координатных осей и:
- •3) Асимптоты гиперболы:
- •4) Фокусы гиперболы:
- •Вывод уравнения параболы
- •Исследование свойств параболы
- •Линии второго порядка в элементарной математике
- •Пункт 1.2. Методические аспекты изучения линий второго порядка в школьном курсе алгебры 7-9 классов
- •1.2.2. Анализ комплектов учебников под редакцией г. В. Дорофеева и ш. Ф. Алимова
- •Глава II. Практическое применение икт при изучении линий второго порядка
Пункт 1.2. Методические аспекты изучения линий второго порядка в школьном курсе алгебры 7-9 классов
1.2.1. Методика изучения линий второго порядка в школьном курсе алгебры
Изучение линий второго порядка в школьном курсе алгебры начинается с 9 класса, I четверти. Где данной теме уделяется 20 часов.
Примерное распределение учебного материала
(Всего на тему отводится 20 ч)
|
Название пунктов в учебнике |
Число уроков |
|
2.1. Какую функцию называют квадратичной |
3 |
|
2.2.
График и свойства функции;
|
3 |
|
2.3.
Сдвиг графика функции
|
4 |
|
2.4.
График функции;
|
5 |
|
2.5. Квадратные неравенства |
4 |
|
Зачет |
1 |
Линии второго порядка задаются квадратичной функцией. Не смотря на чрезвычайно большой объем, широту и сложность понятия функции, его простейший вариант дается уже в средних классах школы. Это понятие в дальнейшем играет важную роль, являясь базовым понятием в изучении алгебры и начал анализа. Начиная с 7 класса средней школы идет постепенное изучение свойств функций и функциональных зависимостей. Рассматриваются различные классы функций: начиная с простейших линейных функций и их графиков, затем следуют квадратичные функции, функции обратной пропорциональности и дробно-линейные функции.
В данной работе подробно рассмотрим особенности изучения учащимися квадратичной функции и выражающей обратно пропорциональную зависимость.
К изучению класса квадратичных функций учащиеся знают, как строить график линейной функции:
метод «загущения» точек на графике;
построение по двум точкам;
Однако для построения параболы нужны новые приёмы:
c)
приём, основанный на преобразования,
задающего функцию, к виду
 ,использовании
геометрических преобразований для
построения графика произвольной
квадратичной функции из параболы
стандартного вида - графика функции
,использовании
геометрических преобразований для
построения графика произвольной
квадратичной функции из параболы
стандартного вида - графика функции
 ;
;
построение по характеристическим точкам и с учетом свойств симметрии. При построении графика функции необходимо использовать следующий алгоритм:
Выяснить направление ветвей. Если
 ,
то ветви параболы направлены вверх,
если
,
то ветви параболы направлены вверх,
если ,
то ветви направлены вниз.
,
то ветви направлены вниз.Вычислить координаты вершины параболы
 по формулам
по формулам и
и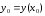 .
.Найти нули функции
 и построить на оси абсцисс соответствующие
точки параболы.
и построить на оси абсцисс соответствующие
точки параболы.Вычисляем координаты точки пересечения параболы с осью ординат:
 и
строим точку, симметричную ей относительно
оси параболы.
и
строим точку, симметричную ей относительно
оси параболы.Через построенные точки проводим параболу.
Квадратичная функция вводится и изучается в тесной связи квадратичными уравнениями и неравенствами.
Первой
из этого класса функций, в значительной
степени еще вне
изучения
собственного класса, рассматривается
функция
 .
По своим
свойствам, прежде всего, эта функция
немонотонна, в отличие от линейной
функции. Чтобы подчеркнуть указанное
отличие, полезно предложить учащимся
следующее задание:
Функция задана
формулой
.
По своим
свойствам, прежде всего, эта функция
немонотонна, в отличие от линейной
функции. Чтобы подчеркнуть указанное
отличие, полезно предложить учащимся
следующее задание:
Функция задана
формулой
 на промежутке
на промежутке
 .
Найти множество значений этой функции.
.
Найти множество значений этой функции.
Перенося
свойство монотонности с класса линейных
функций на
 ,
учащиеся
могут допустить ошибку, именно поэтому
следует
рассмотреть график функции
,
учащиеся
могут допустить ошибку, именно поэтому
следует
рассмотреть график функции
 и
его построение:
и
его построение:
методом «загущения точек;
по характеристическим точкам.
Другое
отличие состоит в том, что характер
изменения значений
функции
 неравномерный:
на одних участках она растет быстрее,
на других - медленнее. Эта особенность
выявляется при построении графика,
причем целесообразно рассмотреть два
графика: один - в крупном масштабе на
промежутке
неравномерный:
на одних участках она растет быстрее,
на других - медленнее. Эта особенность
выявляется при построении графика,
причем целесообразно рассмотреть два
графика: один - в крупном масштабе на
промежутке
 ,
другой—в мелком масштабе на промежутке,
например,
,
другой—в мелком масштабе на промежутке,
например, .
Построение можно вести описанным выше
методом загущения. Важно отметить
свойство параболы
-
симметричность
относительно оси абсцисс. В дальнейшем
это свойство приведет к рассмотрению
класса четных функций, причем именно
функция
.
Построение можно вести описанным выше
методом загущения. Важно отметить
свойство параболы
-
симметричность
относительно оси абсцисс. В дальнейшем
это свойство приведет к рассмотрению
класса четных функций, причем именно
функция
 будет
ведущим примером функции этого класса.
будет
ведущим примером функции этого класса.
Изучение
класса квадратичных функций начинается
с изучения функций вида
 ;
при этом выясняется геометрический
смысл коэффициента а, путем построения
и сравнения нескольких графиков функции
в одной системе координат:
;
при этом выясняется геометрический
смысл коэффициента а, путем построения
и сравнения нескольких графиков функции
в одной системе координат:
 .После
чего рассматриваются свойства функции
при
.После
чего рассматриваются свойства функции
при ,
вводится понятие области определения.
При этом сначала рассуждения проводятся
с использованием геометрической
терминологии и с опорой на график, а
затем те же самые факты формулируются
на алгебраическом языке. Таким образом,
формирование таких понятий, как
наименьшее (или наибольшее) значение
квадратичной функции, неограниченность
сверху (или снизу) происходит с опорой
на наглядные представления. Школьники
должны знать и о симметрии графиков
функции
,
вводится понятие области определения.
При этом сначала рассуждения проводятся
с использованием геометрической
терминологии и с опорой на график, а
затем те же самые факты формулируются
на алгебраическом языке. Таким образом,
формирование таких понятий, как
наименьшее (или наибольшее) значение
квадратичной функции, неограниченность
сверху (или снизу) происходит с опорой
на наглядные представления. Школьники
должны знать и о симметрии графиков
функции
 относительно
оси OX
при противоположных значениях a,
и об изменении «крутизны» параболы при
изменении a.
относительно
оси OX
при противоположных значениях a,
и об изменении «крутизны» параболы при
изменении a.
Далее
вводится более широкий класс функций,
имеющий вид
 .
И здесь также коэффициент
.
И здесь также коэффициент
 получает
ясную геометрическую интерпретацию.
При этом справедливо следующее
утверждение: чтобы построить график
функции
получает
ясную геометрическую интерпретацию.
При этом справедливо следующее
утверждение: чтобы построить график
функции
 ,
гдеc-
заданное положительное число, надо
сдвинуть график функции
,
гдеc-
заданное положительное число, надо
сдвинуть график функции
 вдоль осиOY
на c
единиц масштаба вверх; чтобы построить
график функции
вдоль осиOY
на c
единиц масштаба вверх; чтобы построить
график функции
 ,
гдеc-
заданное положительное число, надо
сдвинуть график функции
,
гдеc-
заданное положительное число, надо
сдвинуть график функции
 вдоль осиOY
на c
единиц масштаба вниз.
вдоль осиOY
на c
единиц масштаба вниз.
Пример
1.
Задан график функции .
Построить на этом чертеже график функции
.
Построить на этом чертеже график функции
 .
.
Заметим,
что при заданном значении аргумента Х0
значения функции
 на
одно и то же число, равное 1, больше
значений функции
на
одно и то же число, равное 1, больше
значений функции .
Поэтому для построения соответствующей
точки второй функции на графике достаточно
поднять на 1 точку график первой функции
с абсциссой Х0.
Следовательно, чтобы построить весь
график второй функции, нужно поднять
на 1 весь график первой функции. Отсюда,
наконец, доказывается теорема о том,
что график любой функции вида
.
Поэтому для построения соответствующей
точки второй функции на графике достаточно
поднять на 1 точку график первой функции
с абсциссой Х0.
Следовательно, чтобы построить весь
график второй функции, нужно поднять
на 1 весь график первой функции. Отсюда,
наконец, доказывается теорема о том,
что график любой функции вида
 может
быть получен путем сдвигов вдоль
координатных
осей параболы
может
быть получен путем сдвигов вдоль
координатных
осей параболы
 .
.
После
этой подготовки, казалось бы, можно
приступить к изучению графиков
произвольных квадратичных функций. Но
здесь возникает трудность: коэффициент
при первой степени неизвестного не
имеет для квадратичной функции
 достаточно простого геометрического
смысла. Именно поэтому приходится идти
обходным путем, следуя тем же
преобразованиям, которые производились
при выводе формулы решения квадратного
уравнения, и вводить в рассмотрение
новый подкласс квадратичных функций
вида
достаточно простого геометрического
смысла. Именно поэтому приходится идти
обходным путем, следуя тем же
преобразованиям, которые производились
при выводе формулы решения квадратного
уравнения, и вводить в рассмотрение
новый подкласс квадратичных функций
вида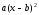 .
Объяснения при построении графиков
здесь в целом могут быть такими же, как
при рассмотрении функций вида
.
Объяснения при построении графиков
здесь в целом могут быть такими же, как
при рассмотрении функций вида
 ,
однако усваивается предлагаемый способ
здесь с большим трудом, так как требует
дополнительных геометрических
преобразований, поэтому требуется
достаточное количество упражнений для
закрепления. После таких приготовлений
построение графика, а также изучение
его свойств происходят без принципиальных
затруднений.
,
однако усваивается предлагаемый способ
здесь с большим трудом, так как требует
дополнительных геометрических
преобразований, поэтому требуется
достаточное количество упражнений для
закрепления. После таких приготовлений
построение графика, а также изучение
его свойств происходят без принципиальных
затруднений.
Отметим здесь один частный, но полезный прием, который состоит в использовании системы заданий, имеющих цель - дать представление о тех или иных чертах данной функции или целого класса без указания точного значения величин, связанных с рассматриваемым вопросом. Этот прием можно назвать качественным или оценочным исследованием функции. Приведем два примера, связанные с изучением квадратичных функций.
Пример
2.
На рисунке изображены графики функций
 и
и
 .
Как относительно их пройдет график
функции
.
Как относительно их пройдет график
функции
 ;
; ;
;
 ?
Это задание не предполагает «точного»
построения искомого графика; достаточно
лишь указание на область, где он
расположен, или его эскизное построение.
?
Это задание не предполагает «точного»
построения искомого графика; достаточно
лишь указание на область, где он
расположен, или его эскизное построение.
Пример
3.
На рисунке изображен график функции
 ,пользуясь
этим чертежом, изобразить от руки график
функции
,пользуясь
этим чертежом, изобразить от руки график
функции
 .
Проверить правильность сделанного
эскиза, вычислить значения функции
.
Проверить правильность сделанного
эскиза, вычислить значения функции
 при
при
 и отметить точки графика. Каким
преобразованием можно перевести график
функции
и отметить точки графика. Каким
преобразованием можно перевести график
функции в
график функции
в
график функции
 ?
?

Рис.3.
График функции

Теперь
учащиеся по коэффициентам квадратного
трехчлена
 могут
представить общий вид соответствующей
параболы и вычислить координаты её
вершины, путём выделения полного квадрата
в данном трёхчлене. В результате
выполнения практических заданий, на
построение графика квадратичной функции
необходимо в строгой последовательности
поговорить и зафиксировать алгоритм
построения функции
могут
представить общий вид соответствующей
параболы и вычислить координаты её
вершины, путём выделения полного квадрата
в данном трёхчлене. В результате
выполнения практических заданий, на
построение графика квадратичной функции
необходимо в строгой последовательности
поговорить и зафиксировать алгоритм
построения функции
 .
.
В системе упражнений значительное место отводится задачам прикладного характера. Завершается тема рассмотрением вопроса о решении квадратных неравенств, выбор решения основан на использовании графиков.
При работе с теоретической частью и выполнении заданий учащиеся должны будут проводить наблюдение, выдвигать гипотезы, рассуждать, доказывать, переходить от одной системы терминов к другой.
Затем отмечается, что график любой квадратичной функции - это парабола и приведены различные виды парабол.
В
восьмом классе идет изучение функции ,
изложение материала
начинается
с анализа примеров реальных зависимостей.
Учащимся предлагается рассмотреть
зависимость времени движения пешехода
от его скорости, длины стороны
прямоугольника заданной площади от
длины другой его стороны, количества
товара, которое можно купить на
определенную сумму денег, от цены этого
товара. Обобщая эти примеры
постепенно
приходим к определению функции
,
изложение материала
начинается
с анализа примеров реальных зависимостей.
Учащимся предлагается рассмотреть
зависимость времени движения пешехода
от его скорости, длины стороны
прямоугольника заданной площади от
длины другой его стороны, количества
товара, которое можно купить на
определенную сумму денег, от цены этого
товара. Обобщая эти примеры
постепенно
приходим к определению функции
 (называемой
обратной
пропорциональностью).
(называемой
обратной
пропорциональностью).
Все
свойства и график функции в учебнике
рассматриваются на примере
конкретных
функций (Например,
 ).
По
точкам строится график
данной
функции и вводится его название
(гипербола). Здесь из свойств выделяются
только область определения, промежутки
убывания и возрастания функции и делается
замечание, что график данной функции
не пересекает координатные оси.
Исследование проводится подробно для
первого случая, когда
).
По
точкам строится график
данной
функции и вводится его название
(гипербола). Здесь из свойств выделяются
только область определения, промежутки
убывания и возрастания функции и делается
замечание, что график данной функции
не пересекает координатные оси.
Исследование проводится подробно для
первого случая, когда
 ,
а для второго случая
(
,
а для второго случая
( )
приведены
только конечные выводы и результаты.
)
приведены
только конечные выводы и результаты.
Традиционно
построение графика обратной
пропорциональности вызывает у учащихся
трудности. Многие строят его небрежно,
не соблюдая симметрии ветвей, ветви
бывают очень короткие, очень часто в
работах учащихся одна из ветвей гиперболы
сначала приближается, например, к оси
х, а затем удаляется от нее. Для
предупреждения подобных ошибок очень
важно проанализировать особенности
графика, обратив внимание учащихся на
то, что график состоит из двух ветвей,
симметричных друг другу относительно
начала координат. Каждая ветвь гиперболы
по мере удаления от начала координат
становится все ближе и ближе к осям, но
не пересекает их. Бесконечное приближение
ветвей к осям координат можно
проиллюстрировать в ходе небольшого
числового опыта: например,
подставить
в формулу вместо х несколько достаточно
больших чисел в порядке их возрастания
и понаблюдать, как изменяется при этом
значение
 .
.


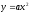 вдоль осей координат
вдоль осей координат