
- •Содержание
- •Г л а в а 6. Элементы и параметры электрических цепей переменного тока
- •Приложение
- •Введение
- •Электростатическое поле
- •1. Закон кулона
- •2. Напряженность электрического поля
- •3. Диэлектрическая проницаемость
- •Контрольные вопросы
- •Проводники в электрическом поле. Цепи постоянного тока. Токопроводящие материалы.
- •1. Электрический ток
- •2. Напряженность электрического поля, потенциал, напряжение и эдс
- •3. Электрическое сопротивление и проводимость
- •4. Закон ома
- •5. Законы кирхгофа
- •6. Соединение резисторов
- •7. Закон джоуля-ленца. Нагревание проводников.
- •8. Короткое замыкание и перегрузки. Тепловая защита.
- •9. Мощность
- •10. Электрические цепи с несколькими источниками энергии
- •11. Делитель напряжения
- •12. Потери напряжения и мощности в проводах
- •13. Передача электрической энергии по проводам
- •14. Токопроводящие материалы
- •Контрольные вопросы
- •Диэлектрики в электрическом поле. Изоляция электротехнических материалов. Диэлектрические материалы.
- •1. Строение диэлектрика.
- •2. Диэлектрик в электрическом поле. Поляризация диэлектрика
- •3. Электрическая емкость. Конденсаторы.
- •4. Соединение конденсаторов
- •5. Энергия электрического поля конденсатора
- •6. Электрический пробой диэлектрика
- •7. Диэлектрические материалы. Изоляция электротехнических материалов.
- •Контрольные вопросы
- •Магнитное поле. Электромагнетизм и электромагнитная индукция. Магнитные материалы.
- •1. Магнитное поле в неферромагнитной среде. Основные понятия
- •2. Напряженность и индукция магнитного поля
- •3. Магнитный поток.
- •4. Индуктивность.
- •5. Магнитные свойства веществ. Магнитная проницаемость
- •Магнитные свойства ферромагнитных материалов. Намагниченность.
- •7. Циклическое перемагничивание. Гистерезис.
- •8. Ферромагнитные материалы
- •9. Электромагнитные силы
- •10. Электромагнитная индукция
- •11. Вихревые токи
- •12. Эдс самоиндукции и взаимоиндукции
- •Контрольные вопросы
- •Линейные электрические цепи переменного тока
- •Основные определения
- •Сложение синусоидальных величин
- •Среднее значение синусоидальных величин
- •Контрольные вопросы
- •Элементы и параметры электрических цепей переменного тока
- •1. Цепь с активным сопротивлением
- •2. Электрическая цепь с индуктивностью
- •Резонанс напряжений
- •Параллельное соединение r, l, c – элементов
- •Контрольные вопросы
- •Трехфазные электрические цепи
- •Принципы построения трехфазных электрических цепей
- •Соединение звезда. Несимметричная нагрузка. Явление перекоса фаз
- •Нулевой провод
- •Мощность трехфазной системы
- •Контрольные вопросы
- •Нелинейные электрические цепи
- •Характеристики нелинейных электрических цепей и элементов
- •Электрическая цепь с нелинейным индуктивным элементом
- •Трансформаторы
- •Контрольные вопросы
- •Электрические машины переменного тока
- •Вращающееся магнитное поле
- •Устройство асинхронного двигателя
- •Принцип работы асинхронного двигателя
- •Регулирование числа оборотов асинхронного двигателя
- •Однофазные асинхронные двигатели
- •Синхронный генератор. Устройство и принцип работы
- •Синхронный двигатель. Принцип работы
- •Контрольные вопросы
- •Машины постоянного тока
- •Общие сведения
- •Устройство и работа генератора постоянного тока
- •Типы генераторов постоянного тока
- •Генератор с независимым возбуждением
- •Генератор с параллельным возбуждением
- •Генератор с последовательным возбуждением
- •Генератор со смешанным возбуждением
- •Двигатели постоянного тока
- •Контрольные вопросы
- •Переходные процессы в электрических цепях
- •Основные определения
- •2. Зарядка и разрядка конденсатора
- •3. Релаксационные колебания
- •4. Включение и выключение реальной индуктивной катушки при постоянном напряжении источника
- •5. Разрядка конденсатора на индуктивность
- •Контрольные вопросы
- •Современные способы получения электрической энергии. Виды силовых электростанций. Альтернативная электроэнергетика.
- •1. Тепловые электростанции (тэс)
- •Экологические проблемы тэс
- •2. Гидравлические электрические станции (гэс).
- •3. Гидроаккумулирующие электрические станции (гаэс)
- •4. Приливные электрические станции
- •5. Атомные электрические станции (аэс)
- •55Cs140→56Ba140→57La140→58Ge140→стабильное ядро;
- •37Rb94→38Sr94→39y94→40Zr90→ стабильное ядро.
- •Магнитогидродинамическое преобразование энергии (мгд-генераторы).
- •7. Термоэмиссионные генераторы
- •8. Солнечные электростанции
- •9. Электрохимические генераторы
- •10. Термоэлектрические генераторы
- •11. Геотермальные электростанции
- •12. Термоядерная энергетика
- •13. Водородная энергетика
- •14. Понятие о единой энергетической системе.
- •Контрольные вопросы
- •Атомно-молекулярная теория строения вещества
- •Структура и строение атома
- •Линейчатый спектр. Постулаты бора и квантование орбит
- •Корпускулярно - волновой дуализм нанообъектов. Волны де-бройля
- •Туннелирование
- •Классификация наноматериалов
- •8. Трехмерные наноматериалы
- •Размерные эффекты и свойства нанообъектов
- •Химические свойства наноматериалов
- •Тепловые свойства нанообъектов
- •Магнитные свойства нанообъектов
- •Функциональные и конструкционные углеродные наноматериалы.
- •Получение углеродных наноструктур
- •Применение и использование наноматериалов в практической деятельности
- •Контрольные вопросы
- •Приложение
- •Сложение векторов.
- •Метод комплексных чисел
- •Расчет цепей методом узлового напряжения
Контрольные вопросы
Почему материалы в масштабе «нано» ведут себя необычно и обнаруживают свойства, отличающиеся от тех, что они имеют в массивом состоянии?
Какие вещества можно использовать в качестве восстановителей при получении наночастиц золота и серебро?
За счет чего происходит процесс стабилизации наночастиц? Для чего это нужно?
Какие частицы называют однодоменными?
Как волновые свойства света и электрона проявляются в экспериментальных наблюдениях?
В чем состоит гипотеза де Бройля?
Какие фундаментальные отличия в заполнении энергетических зон у металлов, диэлектриков и полупроводников?
В чем состоит сущность процесса туннелирования?
В чем состоит квантоворазмерный эффект?
Чем обусловлен предел разрешения электронного микроскопа?
Опишите принцип действия просвечивающего электронного микроскопа.
В чем заключается принцип работы сканирующего зондового микроскопа?
В чем отличие между туннельным и атомно-силовым микроскопом?
Что такое кластер? В чем особенности физических свойств кластеров?
Как получают нанокластеры?
Что такое магические числа?
Что такое квантовые точки и почему их называют «искусственными атомами»?
Что называется аллотропической формой углеродных наноструктур?
Какими способами получают углеродные наноструктуры?
Какие химические свойства углеродных нанотрубок Вам известны?
Приведите примеры использования нанотехнологий в медицине.
Приложение
НЕКОТОРЫЕ СВЕДЕНИЯ О ВЕКТОРАХ.
Величины, характеризующиеся численным значением и направлением, называются векторами. К числу векторов принадлежат скорость, ускорение, сила и ряд других величин. В практике расчетов электрических цепей переменного тока широко используется метод векторных диаграмм, отличающийся простотой и наглядностью. Диаграммы применяют главным образом потому, что сложение и вычитание синусоидальных величин, наиболее просто выполняется в векторной форме. На чертежах векторы изображаются в виде прямолинейных отрезков со стрелкой на конце. Длина отрезка в установленном масштабе дает модуль вектора, а указанное стрелкой направление отрезка дает направление вектора.
Векторы, направленные вдоль параллельных прямых (в одну т ту же сторону или в противоположные стороны), называются коллинеарными.
Векторы, направления которых параллельны одной и той же плоскости, называются компланарными.
Одинаковые по модулю коллинеарные векторы, направленные в одну и ту же сторону, считаются равными друг другу. Равные по модулю коллинеарные векторы, имеющие противоположные направления, считаются отличающимися друг от друга по знаку.
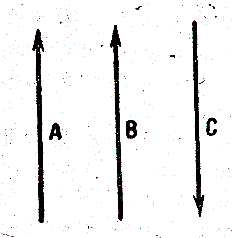 Так,
например, между векторами, изображенными
на рис.224 и их модулями имеются следующие
соотношения:
Так,
например, между векторами, изображенными
на рис.224 и их модулями имеются следующие
соотношения:
А = В; А = -С; В = -С;
А
= В = С или ![]() .
.
Рис.224
Сложение векторов.
Рис. 225
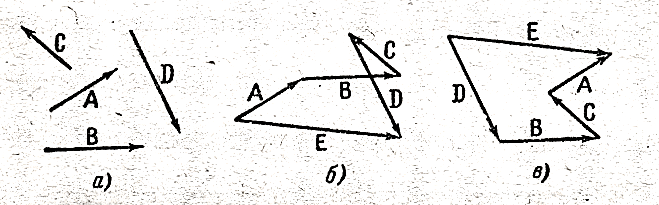
Пусть даны два вектора А и В (рис.225 а). Чтобы получить результирующий вектор С, перенесем вектор В параллельно самому себе так, чтобы его начало оказалось совмещенным с концом вектора А (рис.225 б). Тогда вектор С, проведенный из начала вектора А в конец вектора В, будет представлять собой результирующий вектор;
С = А + В. (п.1)
Можно, однако, осуществить построение несколько иным способом (рис.225 в). Перенесем вектор В (или А) так, чтобы начала обоих векторов оказались совмещенными. Затем построим на векторах А и В параллелограмм. Диагональ этого параллелограмма, очевидно, совпадает с вектором С, полученным по способу, параллельного переноса (рис. б). По этой причине часто говорят, что векторы складываются по правилу параллелограмма.
 Оба
рассмотренных способа дают одинаковый
результат. Однако в случае сложения
более чем двух векторов способ
параллельного переноса (способ (б))
оказывается более простым и удобным
(менее
Оба
рассмотренных способа дают одинаковый
результат. Однако в случае сложения
более чем двух векторов способ
параллельного переноса (способ (б))
оказывается более простым и удобным
(менее
Рис.226
загромождается чертеж). Пусть даны векторы А, В, С и D (рис.226 ). Перенесем векторы параллельно самим себе таким образом, чтобы начало последующего ректора оказалось совмещенным с концом предыдущего.
Получится ломаная линия. Результирующий вектор будет представлять собой вектор Е, проведенный из начала первого из слагаемых векторов А в конец последнего D. Легко убедиться в том, что результирующий вектор Е не зависит от последовательности, в которой складываются заданные векторы. На рис.226 б. показан случай Е = А + В + С + D, а на рис.226 в – случай Е =D+ В + С + А.
 Вычитание
векторов.
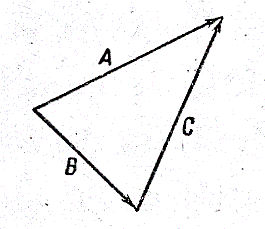
Разностью двух векторов А
– В называется
такой вектор С,
который в сумме с
Вычитание
векторов.
Разностью двух векторов А
– В называется
такой вектор С,
который в сумме с
Рис.227
вектором В дает вектор А (рис.227 ). Поскольку разность А – В может быть представлена в виде
А – В = А + (-В), (п.2)
вектор С =А –В можно получить, сложив вектор А с вектором, равным по величине вектору В, взятому с обратным знаком.
 Радиус
– вектор.
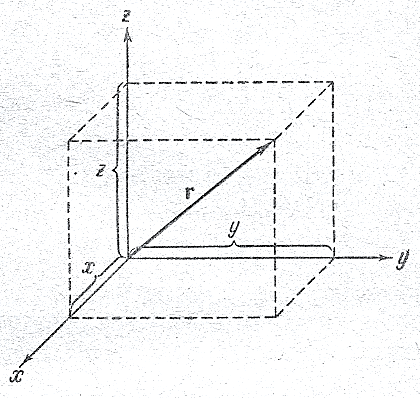
Радиусом – вектором точки называется
вектор, проведенный из начала координат
в данную точку (рис.228). Радиус – вектор
r
однозначно определяет положение точки
в пространстве. Его
Радиус
– вектор.
Радиусом – вектором точки называется
вектор, проведенный из начала координат
в данную точку (рис.228). Радиус – вектор
r
однозначно определяет положение точки
в пространстве. Его
Рис. 228
декартовым координатам точки:
rx = x; ry = y; rz = z. (п.3)
Квадрат модуля вектора r равен сумме квадратов координат:
r2 = x2 + y2 + z2 (п.4).
Проекция вектора на ось.
Пусть даны вектор А
и некоторое направление в пространстве
(ось), которое обозначим буквой n
(рис.229 ). Проведем через началои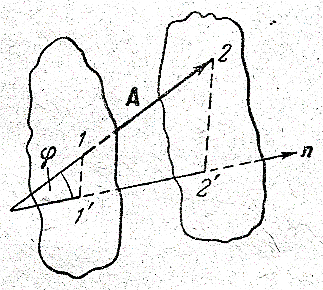 конец вектораА
плоскости, перпендикулярные к направлению
n.
Точки 1' и 2', в которых пересекаются эти
плоскости с осью n,
называются проекциями начала и конца
вектора А на
ось n.
Величина отрезка оси, заключенного
между плоскостями, называется проекцией
вектора А
на направление (или на ось) n.
Проекция вектора есть скалярная
величина. Если направление от точки 1'
к точке 2' совпадает с направлением n,
проекция считается
положительной; в противном случае
проекция отрицательна.
конец вектораА
плоскости, перпендикулярные к направлению
n.
Точки 1' и 2', в которых пересекаются эти
плоскости с осью n,
называются проекциями начала и конца
вектора А на
ось n.
Величина отрезка оси, заключенного
между плоскостями, называется проекцией
вектора А
на направление (или на ось) n.
Проекция вектора есть скалярная
величина. Если направление от точки 1'
к точке 2' совпадает с направлением n,
проекция считается
положительной; в противном случае
проекция отрицательна.
Рис.229
Проекция, обозначается той же буквой, что и сам вектор, с добавлением индекса, обозначающего то направление, на которое спроектирован вектор. Например, проекция вектора А на направление n обозначается Аn.
Введем в рассмотрение угол φ, который образует вектор А с осью n (рис. ). Проекция Аn, очевидно, может быть вычислена следующим образом:
А n = А cosφ, (п.5)
где А – модуль вектора А.
Если вектор образует с данным направлением острый угол, косинус этого угла положителен, проекция вектора также положительна. Если вектор образует с осью тупой угол, косинус этого угла отрицателен, проекция также отрицательна. Если вектор перпендикулярен к данной оси, проекция его равна нулю.
Разложение вектора на составляющие.
Каждый вектор А
можно заменить несколькими векторами
А1,
А2,
и т.д., которые в сумме дают вектор А.
В этом случае векторы А1,
А2
и т.д. называют составляющими вектора
А.
Саму операцию замены вектора А
несколькими
векторами называют разложением вектора
А
на составляющие.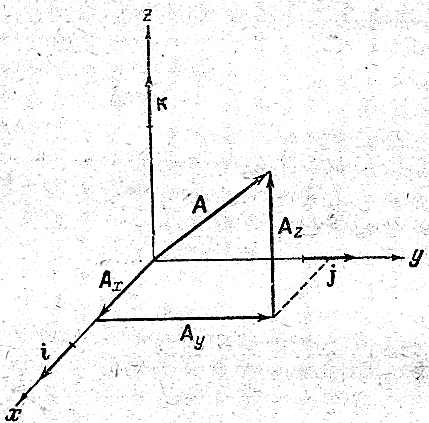
На рис.230 показано разложение вектора А на составляющие, имеющие направления прямоугольных координатных осей. Символами Ax, Ay, Az обозначены составляющие вектора А по осям x,y и z.
Рис.230
