Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Балтийский федеральный университет им. И.Канта

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Попов - весь практикум по геометрии

.pdf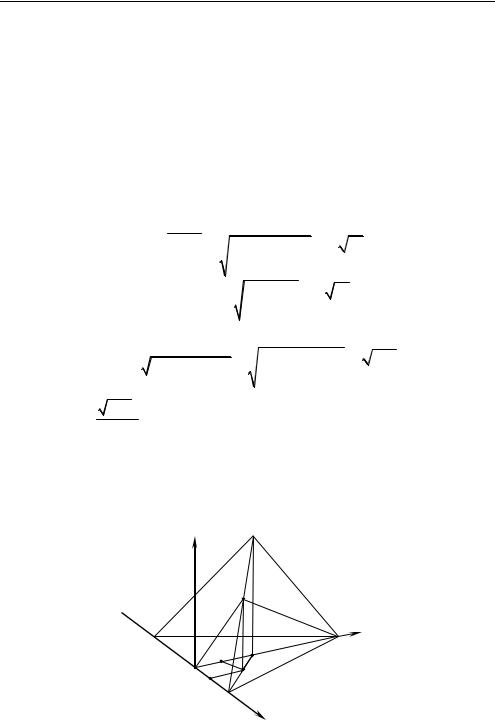

Скачиваний:

179

Добавлен:

10.02.2015

Размер:

16.05 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 198 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Глава I

○ 1. Выберем систему координат так, как указано на рис. 1.12. Найдем координаты точек и векторов относительно выбранной системы

координат:

C (3a ; a ; o ),

B (3a ; o; o ),

;a;a

def

;0;

BM p

;a;a

MC m

a .

2. Пусть K основание перпендикуляра, проведенного из точки C на прямую BM, т. е. KC = h — расстояние от точки C до прямой (BM). Далее вычисляем последовательно:

								9a2			a2
а) MK			p m					4					13a
			p m					4					13a
	орт.прpm														;

													2	17

				p		9a		2	a2 a2
								2

						4
						4
							9a			2	a2	a 13 ;
b) длину отрезка MC					MC		9a				a2	a 13 ;
								4					2
								4					2
с) по теореме Пифагора находим
h KC		MC2 MK2							13a2			169a2			221a	.
h KC		MC2 MK2							13a2			4 17			17	.
											4	4 17			17

Ответ: 221a17 .

Задача 1.3. На ребре правильного тетраэдра MABC взята точка K — середина этого ребра, а на ребре MB взята точка P. Считая ребро тетраэдра равным а, найдите расстояние от точки P до прямой CK, если MP : MB = 1:4 (рис. 1.13).

z		M
z
		P	a
		P
A			C	y
A	N	O	C
	N		a
K
K		P1
N1	B
		x
	Рис. 1.13

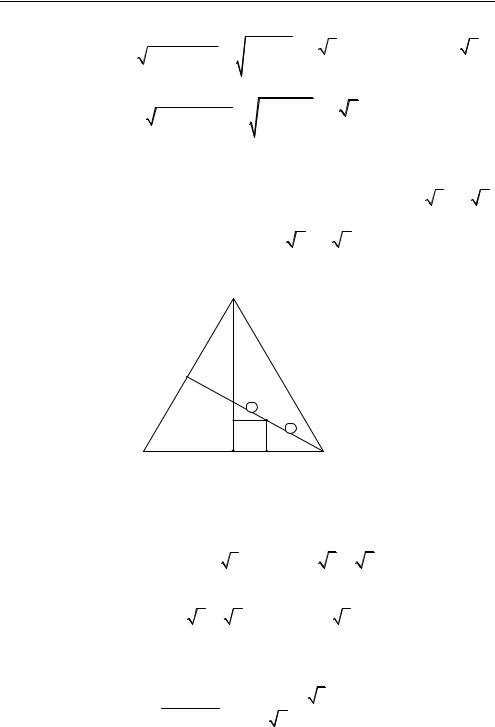
§1.2. Расстояние от точки до прямой. Расстояние от точки до плоскости

1.Произведем предварительные вычисления:

		2				2			2			a2	a 3				2	a 3
а) CKB : KC	CB		KB					a				4	2		OC		3 KC	3
(по свойству медиан правильного треугольника ABC).
				2			2				2	3a2		a	6
b) MOC : MO	MC				OC					a		9			3	.

c) Пусть PP1 — перпендикуляр к плоскости (ABC), т. е. PP1 || OM;

( PP1 B BOM) OP1 : P1B 1: 3 KN1				: N1B 1: 3 и		NO : NK 1: 3.
Отсюда получаем, что KN1	1 KB	a	и	NK	3 KO	3	a	3 a 3
	4	8			4	4	6	8
(рис. 2.14). Кроме того, PP	3 OM	3 a	6 a		6 .
1	4	4	3	4
	4	4	3	4

N O1 P1 3

A	K N1	B
	Рис. 1.14

2. Выберем систему координат так, как указано на рис. 1.13. Отно-

сительно выбранной системы координат имеем:
	K(o;o;o;), C(o;								a	3				a		;	a 3			;	a	6	,
	K(o;o;o;), C(o;									2		; o), P			8	;	8			;		4	,
										2					8		8					4
		a			;	a	3	;	a		6							a		3
	KP		8		;		8	;		4			; KC			o;			2			;o .
			8				8			4									2
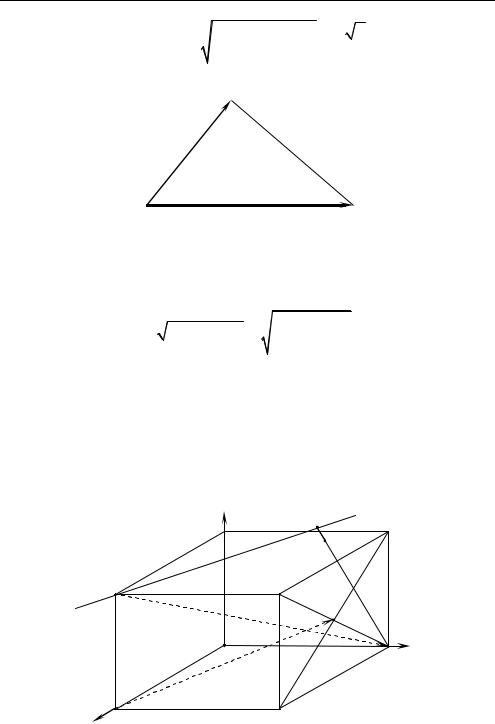
3. Пусть точка F — проекция точки P на прямую KC (рис. 1.15). Тог-

				KP			KC						3a	2			3a		.
да KF	орт.прKC KP


						KC					16 a 3						8
														2

Глава I

2 7a .

Рис. 1.15

7. Из прямоугольного треугольника KFP находим расстояние от точки P до прямой KC:

h PF	KP2 KF2		28a	2		3a2		5a	.
			64			64		8

	5a
Ответ:	8 .
Задача	1.4. Точка O — центроид грани CC1D1D куба

ABCDA1B1C1D1. Считая ребро куба равным а, найдите расстояние

от точки D до прямой , проходящей через вершину B1 параллельно прямой BO (рис. 1.16).

		z		M	l
				M	D1
					D1
	B1		C1		a
					O
		A			D	y
					D	y
					a
	B	a	C
x		a	C
x
		Рис. 1.16

§ 1.2. Расстояние от точки до прямой. Расстояние от точки до плоскости

○ 1. По условию \|\| (BO) и		def
○ 1. По условию \|\| (BO) и	BO \|\| (BO).	Следовательно, BO p —

направляющий вектор прямой . Выберем декартову систему координат так, как указано на рис. 1.16. и найдем координаты следующих точек и векторов в этой системе координат:

B1(a;o;a), D (o; a ; o ),	B(a; o; o),	a		;a;	a	,
		O	2		2

def

B1D (

a; a; a ),

;a;

2. Пусть DM — это перпендикуляр к прямой l , тогда

B1D p

6 .

B1M

орт.прp B1D

a2 a

B D

a2 a2

a 3.

B D

По

теореме

Пифагора

из

B1MD

находим

DM B1D2 B1M2 a 321 .

Ответ: a 21 . 3

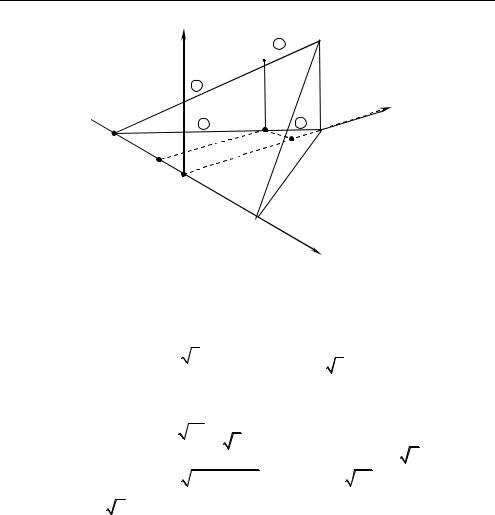
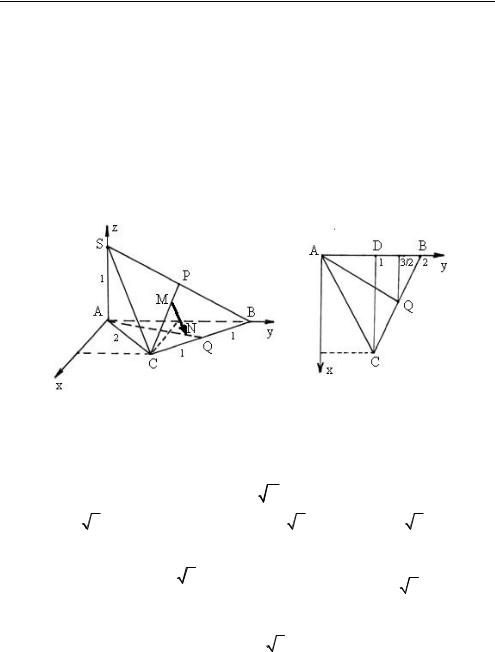
Задача 1.5. Основание пирамиды MABC является правильный треугольник, ее боковое ребро MC перпендикулярно плоскости основания, и MC = AB. Считая AB = a, найдите расстояние от точки P MA до плоскости , проходящей через точку A перпендику-

лярно ребру MB, если MP : PA 1: 3 (рис. 1.17).

○ 1. В

выбранной

системе координат (см. рис. 1.17) находим

координаты следующих точек и векторов:

a 3

3 3a

;o;o

; A

; o;o

, M o;

, P

;

def

;

— нормальный

вектор

плоскости

(из

BM n

условия).

Глава I

z				M
		1		M
	P	1
3				a
3
3	Р1		1	y
3	Р1		1	C
A				C
K			a
a
2
	B

Рис. 1.17

2. Найдем уравнение плоскости по точке A и нормальному вектору n :

:	a		a	a 3y	az	0	2x 2 3y 4z a 0 .
:	2	x		2	az	0	2x 2 3y 4z a 0 .
	2		2	2
Расстояние от точки P до плоскости найдем по формуле (16) (§ 1.2):
			2a	3 3a	2 3	4	3 a a
			2a	3 3a	2 3	4	3 a a
P;			8	8			4		9a	9 2a .
P;				4 12 16				2	32	9 2a .
				4 12 16				2	32	16

Ответ: 9162a .

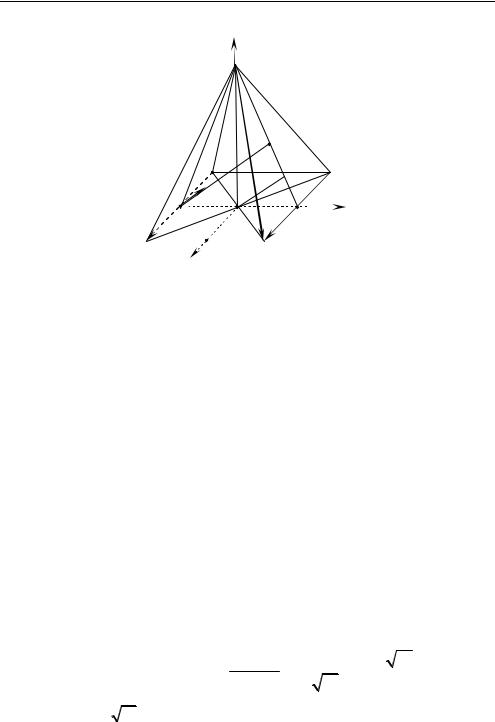
Задача 1.6. В правильной пирамиде MABCD высота MO в два раз больше стороны основания. Считая AB = a, найдите расстояние от точки M до плоскости, проходящей через прямую AD перпендикулярно плоскости MBC (рис. 1.18).

○ 1. В системе координат, указанной на рис. 1.18, найдем координаты следующих точек и векторов:

M(o;o;2a), P

;

, B

, N o;

;

; 2a

; PB

;o;o

, NA

;o;o


;o ,

		a	;2a
NM	o;	2	;2a	.
		2

§ 1.2. Расстояние от точки до прямой. Расстояние от точки до плоскости

N m

2a E

K C

O	a/2	P	y
	a/2

Рис. 1.18

2. Пусть — плоскость, проходящая через прямую AD, и ,

где ( M B C ). Обозначим через

m ( x ; y; z ) — нормальный вектор

плоскости , тогда m MB, m

PB :

a x

a y

2az 0,

x 0,

m MB 0

у 4z

0;4;1 .

m PB 0

a x

3. Так как

обозначим через n (x1, y1,z1)

—

( m

, ) m || .

нормальный вектор плоскости :

z 0,

1;4 .

x1 0

4y1

4. Пусть ( M , ) —

расстояние

от

точки

до

плоскости

которое найдем по формуле (8) (§ 1.1).

NM n

17a

(M, )

орт.прn NM

Ответ:

17a .

Глава I

§1.3. Расстояние между скрещивающимися прямыми

Задача 1.7. В основании треугольной пирамиды SABC лежит правильный ABC со стороной, равной 2. Ребро SA перпендику-

лярно плоскости основания и SA = 1. Точки P и Q соответственно середины ребер SB и CB. Найти расстояние между скрещивающимися прямыми CP и AQ.

○ Построим прямоугольную систему координат так, как указано на рисунке 1.19.

										Рис. 1.19
○ 1-й способ.
а) В этой системе координат находим:
				А(0;0;0), В(0;2;0), С(									3; ;1;0), S(0;0;1),
	(											(				3;				(	3;1; 0).
AC	(		3; 1; 0), AB		(0; 2; 0), CS							(				3;		1; 1), CB		(	3;1; 0).
Отсюда следует, что
		1				3		3							1							1
AQ			AC	AB			;			; 0	, CP					CS			CB		3; 0;		,
AQ		2	AC	AB		2	;	2		; 0	, CP				2	CS			CB		3; 0;	2	,
		2				2		2							2							2
							1							3		1
					CQ				CB						;		; 0	.
					CQ		2		CB					2	;	2	; 0	.
							2							2		2

б) Пусть [MN] — общий перпендикуляр прямых CP и AQ (рис. 1.19).

По правилу многоугольника сложения векторов:

M N M C C Q Q N .

§ 1.3. Расстояние между скрещивающимися прямыми

Учитывая, что
											1 x
MC	║CP	MC	x CP					3x; 0;			1 x	,
											2
								3		3
QN ║ AQ		QN	y AQ						y;		y; 0	,
QN ║ AQ		QN	y AQ					2	y;	2	y; 0	,
								2		2
получим
			3		3
MN	3x		3	y	3		; 1 3 y;				1 x .
MN	3x			y			; 1 3 y;				1 x .
			2			2		2	2		2
			2			2		2	2		2

в) По свойству общего перпендикуляра прямых:

				1			3
MN	AQ 0,	x			y				y 0,
MN	AQ 0,	x		2	y		2		y 0,
				2			2
MN	CP 0
			6 6 y x 0
		12x	6 6 y x 0
						6
x 2 y,		x						,
x 2 y,		x				10		,
						3
13x 6 y 6						3
		y						.
		y				10		.
						10

Из (17), в силу соотношений (18), окончательно имеем

	3		1		6
MN		;		;		.
MN	20	;	20	;	20	.
	20		20		20

(17)

(18)

		1		40	10

Отсюда MN	MN		3 1 36			. ●
		20		20	10

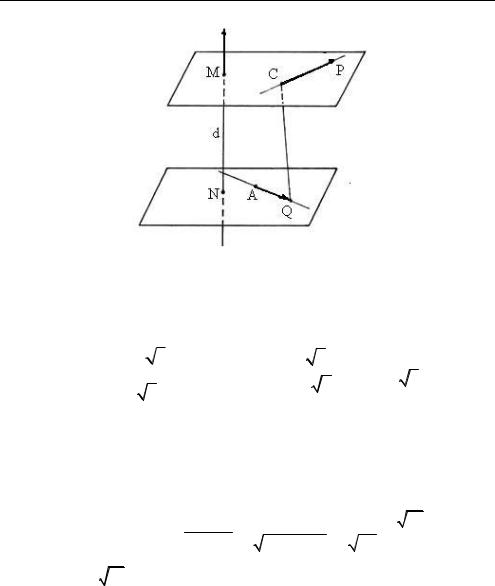
○ 2-й способ.

Известно, что скрещивающиеся прямые лежат в параллельных плоскостях. Пусть (CP) , а (AQ) (рис. 1.20). Тогда расстоя-

ние d MN между плоскостями и есть расстояние между скрещивающимися прямыми CP и AQ.

а) Вводим систему координат так же, как и в пункте 1 а), и находим

		1			3		3			3 1
									, CQ
CP	3; 0;	2	,	AQ	2	;	2	; 0	, CQ	; ; 0	.
		2			2		2			2 2

Глава I

Рис. 1.20

б) Пусть n (x; y; z) — нормальный вектор плоскостей и . В силу этого имеем

			0,			3x		1 z 0,		z	2	3x,
n	CP		0,					2						3; 1; 6 .
					3		3					3 n		3; 1; 6 .
n		AQ		0						y			x
n		AQ		0
						x			y 0			3

					2		2
					2		2

в) Берем любые две точки на скрещивающихся прямых, например C (CP), Q ( AQ) , и по формуле (9) вычисляем расстояние между

этими прямыми:

						n	3	1	0
							3	1
				CQ			2	2		2	10
				CQ			2	2		2	10
d	орт.прnCQ				n							. ●
							3 1 36			40	10


Ответ:		10	.
Ответ:		10	.
		10

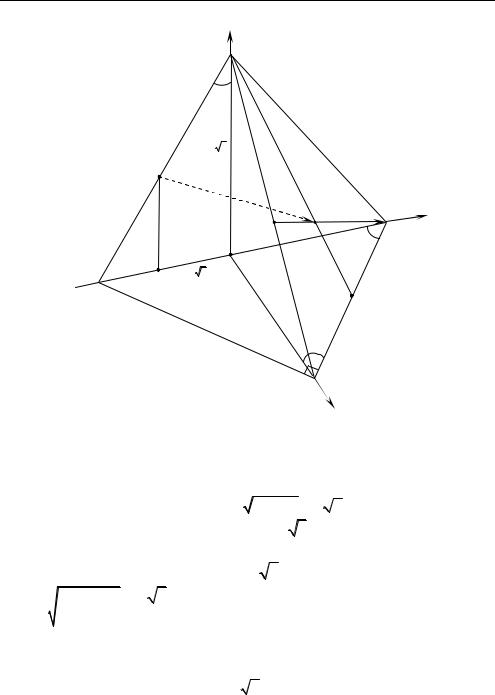
Задача 1.8. В основании пирамиды MABC лежит равнобедренный треугольник с прямым углом при вершине С. Боковая грань MAB перпендикулярна плоскости основания, и в MAB : MAMB. На ребре BM взята точка P — середина этого ребра, а в гра-

ни MAC взята точка Q — центроид этой грани. Найдите расстояние между прямыми AB и PQ, если BC = a и cos AMB 12 (рис. 1.21).

§ 1.3. Расстояние между скрещивающимися прямыми

30°

a 6 2

					Q	A	y
							y
			N			45°
			N
		P1	a 2
	B	P1	2
	B					a
						a
			a
					45°
					C
					x
			Рис. 1.21
		1
○ 1. а) cos AMB		2
○ 1. а) cos AMB		2	AMB 60 NMA			BMN 30 (MA MB).
b) CA B : BC A C a , AB a 2				a 2	a	2 . Так как AM B —
равнобедренный ( M A M B ), то BN a					2 ;
				2
с)		30 , то BM a		2; по теореме Пифагора имеем
с)	BNM : BMN	30 , то BM a		2; по теореме Пифагора имеем
MN	2a2 2a2 a 6 .
	4	2
е) CN — медиана равнобедренного CBA, значит, она является и бис-

сектрисой ВСА 90 , т.е. NCA 45 . Отсюда следует, что ANC —

равнобедренный, т. е. NC NA a 22 .

2. Относительно выбранной системы координат (рис. 1.21) найдем координаты следующих точек и векторов:

<<< < Предыдущая 1 2 3 4 5 6 78 / 198 9 10 11 12 13 14 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.12.201834.55 Кб5Полулях, психология.docx
#
10.02.201531.31 Кб7помощь на защите 1.docx
#
10.02.201561.95 Кб33Понятие об общении коммуникативные умения (1).doc
#
02.09.2019117.93 Кб1попа.docx
#
20.09.201969.63 Кб3ПОПД.doc
#
10.02.201516.05 Mб179Попов - весь практикум по геометрии.pdf
#
10.02.20157.78 Mб100Попов - все лекции по геометрии.pdf
#
10.02.2015152.58 Кб68Портфолио к экзамену Дошк пед.doc
#
10.02.20151.95 Mб105портфолио ученика.doc
#
10.02.201514.08 Кб17Пословицы и поговорки.docx
#
17.08.20194.52 Mб81Пособие 2 студентам по ХТ.doc

○ 1. По условию \|\| (BO) и		def
○ 1. По условию \|\| (BO) и	BO \|\| (BO).	Следовательно, BO p —