
Попов - весь практикум по геометрии
.pdf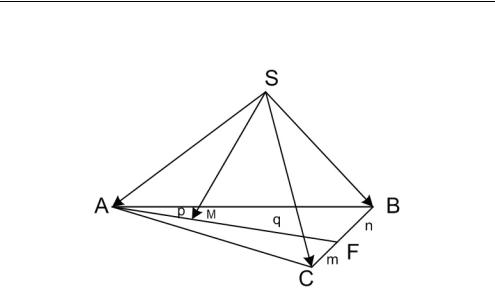
Глава III
Возможны следующие случаи.
1. Точка М — внутренняя точка ∆ АВС (рис. 3.14).
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.14 |
|
|
|
|
|
|
|
|
||||
Пусть точка |
F делит |
BC в отношении, |
CF : FB m : n, а |
|||||||||||||||||||||
точка M делит |
AF в отношении AM |
|
: MF p : q. |
|
|
|||||||||||||||||||
Рассматривая ( SCB ) , по первому основному |
|
векторному |
||||||||||||||||||||||
соотношению находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
n |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
SF |
|
|
|
|
|
|
SB |
|
|
|
|
|
SC. |
|
(2) |
|||
|
|
|
|
|
|
|
m n |
m n |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Теперь рассмотрим плоскость SAF . Вновь применяя первое век- |
||||||||||||||||||||||||
торное соотношение, имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
p |
|
|
q |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
SM |
|
|
|
|
SF |
|
|
|
|
SA. |
|
(3) |
||||||
|
|
|
|
|
|
|
p q |
|
p q |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставим (2) в равенство (3): |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
p |
|
|
|
|
|
|
|
pm |
|
|
|
|
|
|
|
pn |
|
|||||
SM |
|
|
|
|
SA |
|
|
|
|
|
|
|
|
|
SB |
|
|
|
|
|
SC. |
|||
|
p q |
|
( p q)(m n) |
( p q)(m n) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
, |
|
|
|
pm |
|
, |
|
|
pn |
|
|
||||||||
|
p q |
( p |
q)(m n) |
|
( p q)(m n) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
и, следовательно, q(m n) pm n |
1. |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
( p q)(m n) |
|
|
|
|||||||||
94
§3.3. Третье основное векторное соотношение
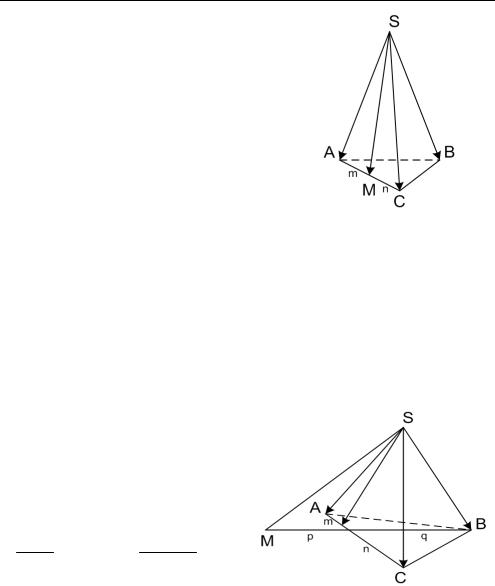
2.Точка М лежит на одной из сто-
рон ∆ АВС.
Пусть для определенности
М АС (рис. 3.15).
Положим АМ : МС m : n , тогда по первому векторному соотношению:
|
|
m |
|
|
n |
|
|
|
SM |
|
|
SC |
|
|
SA 0 |
SB |
|
m n |
m n |
|||||||
|
|
|
|
|
|
|||
и |
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
n |
|
0 1. |
|
|
|
||||||||
|
|
|
m n |
|
m n |
|
Рис. 3.15 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Точка M ∆АВС (рис. 3.16). |
|
|
|
||||||||||||||||||||
|
|
Пусть |
AF : FC |
|
m : n, |
а M F : FB p : q . С одной сторо- |
||||||||||||||||||
ны, рассматривая плоскость SAC , по первому основному векторному |
||||||||||||||||||||||||
соотношению имеем |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
n |
|
|||||||||
|
|
|
|
|
|
|
|
|
SF |
|
|
|
|
|
|
|
SC |
|
SA. |
(4) |
||||
|
|
|
|
|
|
|
|
|
|
m n |
m n |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
С другой стороны, рассматривая плоскость SMB, по формуле (2) |
|
||||||||||||||||||||||
находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
p |
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
SF |
|
|
|
SB |
|
|
|
|
|
SM . |
|
|
|
(5) |
|
|
|
|
|||||
p q |
|
p q |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Из равенств (4), (5) следует: |
|
|
|
|
|
|
|||||||||||||||||
|
q |
|
p |
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
||||||
|
|
SM |
|
|
|
SB |
|
|
|
|
|
|
|
SC |
|
|
|
|
|
|
|
|||
|
p q |
|
p q |
|
|
m n |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
nn( p q)
m n SA SM (m n)q SA
|
p |
m( p q) |
|
|
|||||
|
|
SB |
|
SC. |
|
|
|||
q |
(m n)q |
|
Рис. 3.16 |
||||||
|
|
|
|
|
|
|
|||
Сумма коэффициентов этого равенства |
|
||||||||
|
|
|
|
|
n( p q) |
|
p |
m( p q) |
1. |
|
|
|
|
|
|||||
|
|
|
|
|
(m n)q q |
(m n)q |
|
||
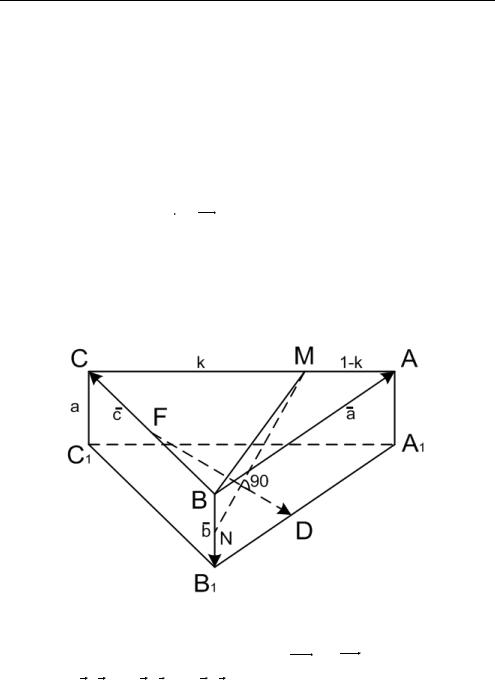
Задача |
3 . 1 3 . В правильной призме АВСА1В1С1 длина сторо- |
||||||||
ны основания равна 4а, длина бокового ребра равна а. Точки D
95
Глава III
и F — середины ребер A1B1 |
и BC соответственно. Отрезок MN с |
||||||||||||||
концами на прямых |
AC |
и |
BB |
пересекает прямую |
DF |
и перпенди- |
|||||||||
|
|
1 |
|
||||||||||||
кулярен к ней. Найти длину этого отрезка. |
|
|
|
|
|
||||||||||
Выберем аффинный базис следующим образом: |
ВА |
а, ВВ1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в, ВС |
с (рис. 3.17). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) Пусть СМ : СА к, BN : BB1 |
l , тогда MA : СА 1 к. |
|
|||||||||||||
По условию |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
(6) |
|||||||
|
|
|
MN FD MN |
FD 0. |
|
|
|
|
|||||||
Выразим векторы MN и FD через базисные векторы a,b, c : |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
MN |
BN |
BM |
lb ka (k 1)c, |
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
(7) |
||
|
|
|
|
|
|
||||||||||
|
FD |
FB BB1 B1D |
2 |
c b |
2 |
a. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 3.17 |
|
Подставим разложения (7) векторов MN и |
FD в равенство (5) и |
учтем, что a b 0, b c 0, a c 8a 2 . |
|
В результате получим: |
|
l 8k 4 0. |
(8) |
96

§ 3.3. Третье основное векторное соотношение
Прямые NM, FD пересекаются, и, |
следовательно, точки F, M , |
||||||||||
N, D лежат в одной плоскости. Значит, |
можно применить третье ос- |
||||||||||
новное векторное соотношение: |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
|
|
|
1 |
|
BM BF BN BD |
|
2 |
c |
(lb) (b |
2 |
a) |
|||||
|
|
|
|
|
|
|
|
|
(9) |
||
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
||||||
|
2 |
a ( l )b |
|
2 |
c, |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
где |
1. |
|
|
|
|
|
|
|
|
|
|
С другой стороны, по первому основному векторному соотношению: |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BM |
k a (1 k)c . |
|
|
(10) |
||||
Из равенств (9) и (10) в силу однозначности разложения вектора по
базису получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
, |
|
|
2(1 k), |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
к |
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
||||||
|
|
l 0, |
|
|
l |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 k ; |
|
|
|
2k. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2k |
|
|
|
|
|
|
|
|
|
||
Из условия 1 2(1 k ) 2k |
|
1 следует |
|||||||||||||||||||||||||||
|
l |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
l 2k 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11) |
|||||
c) Решим систему, составленную из уравнений (8) и (11): |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
l |
2k 0, |
|
|
|
k |
|
3 |
, |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
8k 4 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
l |
|
|
|
|
|
4 |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда из соотношения (7) находим MN |
2 a |
|
4 |
b |
1 c . |
||||||||||||||||||||||||
Отсюда следует: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
MN |
2 |
2 |
( |
2 |
|
4 |
|
|
1 |
|
2 |
|
|
4 |
16a |
2 |
|
16 |
a |
2 |
|
||||||||
|
MN |
3 |
a |
3 |
b |
3 |
c) |
|
9 |
|
9 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
169 a2 94 8a2 1289 a2 MN 8 32 a.
Ответ: MN 8 32 a .
97
Глава III
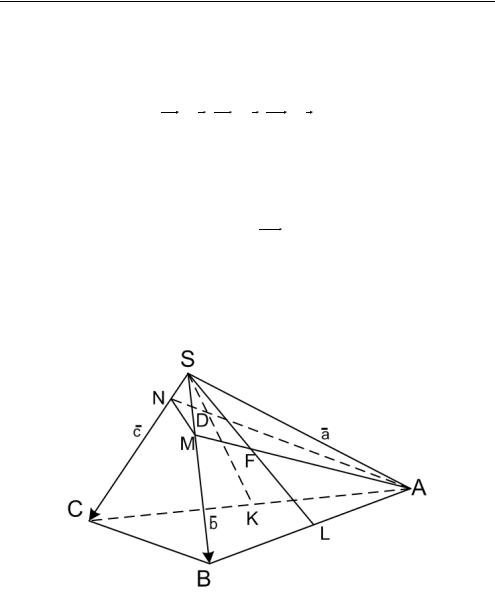
Задача 3 . 1 4 . Секущая плоскость проходит через вершину
Аоснования треугольной пирамиды SABC и делит пополам ме-
диану SL грани SAB , а медиану SK грани SAC пересекает в точке D такой, что DK 2SD . В каком отношении эта плоскость делит ребра грани SBC .
Выберем базис SA a, SB b, SC |
c (рис. 3.18). |
|
||
Пусть |
|
|
|
|
|
(12) |
|||
|
SM xb, SN yc, |
|||
где M и N — точки пересечения секущей плоскости с ребрами SB и |
||||
SC соответственно. Найдем x и |
y в равенствах (12). |
|
||
Представим разложение вектора SM по базису a,b, c , используя |
||||
третье основное векторное соотношение. Действительно, имеем |
||||
|
|
|
|
|
SM |
SA SF |
SD, |
(13) |
|
1. |
|
|||
|
|
|||
|
|
|
|
|
|
|
Рис. 3.18 |
|
|
|
|
|
|
||||
|
Подставим разложения |
векторов |
|
|
|
|
(13) и, учитывая |
||||||||||
|
|
|
SF, SD в |
||||||||||||||
|
1 , получим окончательно: |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
1 |
(1 |
|
|
|
||||
|
SM |
a |
4 |
(a b) |
6 |
)(a |
c) |
(14) |
|||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
5 |
|
1 |
|
|
|
|
|
1 |
|||||||
|
|
|
|
|
|
|
|
||||||||||
|
( |
|
|
|
|
|
)a |
|
|
b |
|
|
c. |
|
|||
|
6 |
4 |
6 |
4 |
|
6 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
98

§ 3.3. Третье основное векторное соотношение
Из равенств (12) и (14) на основе единственности разложения вектора по базису получим систему:
|
|
|
5 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
x |
|
|
, |
|
|
|
|
||||||||
|
|
|
6 |
12 |
6 |
|
|
3 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|||||
|
|
|
|
|
x, |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
||||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
1 |
(1 |
) 0 |
|
|
|
|
|
|
|
|
. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Кроме того, |
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
SF |
2 |
SL |
4 |
(a |
b), SD |
3 |
SK |
|
6 |
(a c). |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Итак, SM 1 |
SB SM |
1 |
SB SM : MB 1 : 2 . |
|
|
||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично находим |
|
y . По третьему основному векторному соот- |
|||||||||||||||||||||||||||||
ношению: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
SN |
SA SF |
SD |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
(15) |
||
|
a |
|
4 |
|
(a |
b) |
6 (1 )(a |
c) . |
|
||||||||||||||||||||||
Из равенств (12) и (15) следует: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
5 |
|
|
1 |
|
1 |
0, |
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
6 |
12 |
|
6 |
|
|
|
|
5 |
, |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
y |
|
y |
|
. |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
(1 ) |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда получаем SN |
|
|
1 |
SC |
и, значит, |
SN : NC 1: 4 . |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
SN : NC 1 : |
4, SM : MB 1 : |
2 . |
|
|
||||||||||||||||||||||||||
Задача |
3 . 1 5 . |
|
Дан куб |
АВС |
1В1С1D1 DсАребром, |
равным a. |
|||||||||||||||||||||||||
Точка K — середина ребра |
AA1 , M — центроид грани (CDD1 ) . |
||||||||||||||||||||||||||||||
Отрезок FH |
с концами на B1C1 |
|
и AD пересекает KM |
и перпен- |
|||||||||||||||||||||||||||
дикулярен ей. Найти длину FH |
|
(рис. 3.19). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
99
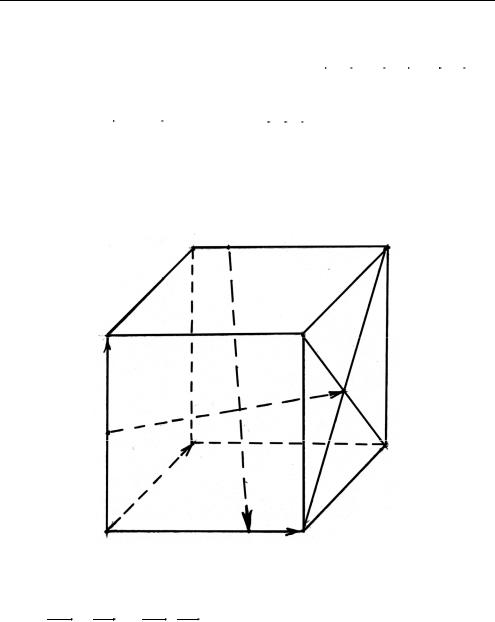
Глава III
1. Центроид M — точка пересечения диагоналей C1D и D1C
C1M MD D1M MC .
2.Выберем базис следующим образом: AD а, AВ в, AA1 с.
Пусть B1F : FC1 l : (1 l) , AH : HD m : (1 m ) .
Выразим FH и KM через базис a , b , c :
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
|
1 |
|
|||||
KM |
KA |
A D |
D M |
|
c a |
|
b |
|
c a |
|
b , |
|||||||||
|
|
1 |
|
1 |
1 |
|
1 |
|
|
2 |
|
|
2 |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
FH |
FB1 |
B1 A1 |
|
A1 |
A |
|
AH |
a(m l) b c . |
|
|||||||||||
|
|
|
|
|
В |
1 |
l |
F |
|
|
1 – l |
|
|
|
|
|
С1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
А1 |
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М |
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
|
|
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
m |
a |
H 1 – m |
D |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
Рис. 3.19 |
|
|
|
|
|
|
|
|
По условию |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
KM FH |
|
|
|
|
|
1 |
|
|
|
|
0 |
|||
KM FH 0 (a |
2 |
b)(a(m l) b c) |
||||||||||||
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
2 |
|
1 |
2 |
0 |
m l |
1 |
|
0. (16) |
||
(m l)a |
2 |
b |
(m l)a |
2 |
a |
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Прямые КМ и FH пересекаются, то есть точки K , M , F , H |
принад- |
|||||||||||||
лежат одной плоскости. Можно применить третье основное векторное соотношение:
100

§ 3.3. Третье основное векторное соотношение
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
D1H |
|
D1K |
D1F D1M |
|
1 |
|
|
|
|
|
|
(17) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
( |
1 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
( a |
2 |
c) |
(b (1 l)a |
2 |
|
b |
2 |
c), |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
С другой стороны, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
D1 H |
|
m c |
(1 m )( a |
|
c). |
|
|
|
|
|
|
|
(18) |
||||||||||||||||
Из (17) и (18) в силу однозначности разложения вектора по базису: |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2m 2l 4 |
, |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
|
|
|
|
|
1 l |
|
|
|
|
|
|
|||||||
|
|
|
|
(1 l) m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
y 2. |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2m 2l 4 |
|
2m 2l 4 |
|
|
1 2m 2l |
4 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
1 l |
|
|
|
|
|
1 l |
|
2 2 ( |
|
1 l |
|
|
2) |
1 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
2m 2l 4 |
|
1 |
2m 2l 4 |
2) 1 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 l |
|
|
|
2 ( |
|
1 l |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
m l 2 |
|
0 m l 2 0. |
|
|
|
|
|
|
|
(19) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Из (16) и (19) следует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
l |
1 |
0, |
|
|
|
m 2 |
l, |
|
|
|
|
|
|
|
l 3 , |
|
|
|
|
|||||||||||||
|
|
|
|
m |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 l l |
|
|
|
|
|
5 |
|
|
|
|
|||||||||
|
|
|
|
m |
l 2 0 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
m |
4 |
. |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FH 1 a b c . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Находим длину FH : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 a. |
|||||||||||||
FH 2 |
|
FH 2 |
|
( |
1 a b c) 2 |
|
1 a 2 |
a 2 a 2 |
9 a 2 |
FH |
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
2 |
|
|
||
Ответ: FH |
3 a. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 3.16. В правильной пирамиде |
|
АВСD длина бокового |
||||||||||||||||||||||||||||||||||||
ребра равна 2а и плоские углы при вершине равны, образованные ребрами пирамиды равны 60 . Точки M и N — середины
101
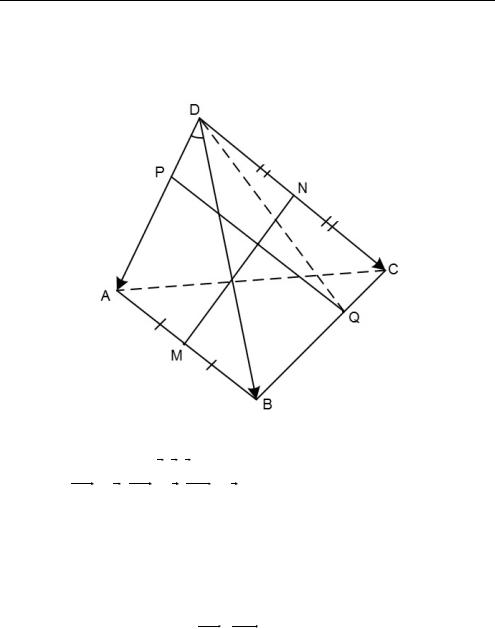
Глава III
ребер AB и DC соответственно. Отрезок PQ с концами на прямых AD и BC пересекает прямую MN и перпендикулярен к ней. Найти длину PQ (рис. 3.20).
a c b
Рис. 3.20
Введем базис a, b, c , как указано на рисунке.
Пусть DA a, DB b, |
DC c . |
|
|
|
|
|
|
|
|
|
||||||
Обозначим DP |
l, |
BQ |
k. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
DA |
|
BC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
1 |
|
1 |
|
|||
MN |
MA |
AD DN |
2 |
(a b) a |
2 |
c |
2 |
c |
2 |
a |
2 |
b; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
PD DQ l |
a k b (1 k) c. |
|
|
|
|
|
|
|
|
||||||
PQ |
|
|
|
|
|
|
|
|
||||||||
Так как PQ MN |
|
PQ MN 0 |
|
l k 0. |
|
|
|
|||||||||
PQ MN (точки P , Q , M , N принадлежат одной плоскости). Применяя третье основное векторное соотношение, находим:
|
|
|
|
|
|
1 |
|
DQ |
DP DB DN |
l a b |
2 |
c, |
|||
|
|
|
1. |
|
|
||
|
|
|
|
|
|||
102

§ 3.3. Третье основное векторное соотношение
Также DQ k b (1 k ) c.
В силу однозначности разложения вектора по базису получаем сле-
дующую систему: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l 0; |
|
0; |
|
|
|
|
|
||||
|
|
k; |
|
|
|
|
|
|
k; |
|
|||
|
1 |
|
|
|
(1 |
k). |
|
|
|
2 |
|||
|
2 |
1 |
k, |
|
|
|
|
|
|
|
|||
|
|
|
k 2 (1 k) 1; |
|
k 1; |
|
|
|
|
|||||
|
|
|
l k 0, |
|
l 1. |
|
|
|
||||||
Тогда PQ a b и PQ |
PQ |
|
(b a) 2 |
4a 2 4a 2 4a 2 2a. |
||||||||||
Ответ: PQ 2a. |
|
|
|
|
|
|
|
|
|
|
|
|||
Задача |
3 . 1 7 . Дана правильная четырехугольная пирамида |
|||||||||||||
SABCD . Сторона основания равна 2a, высота SA равна |
a |
. SA пер- |
||||||||||||
пендикулярна основанию. |
|
M SC, |
N BD, |
MN SC, |
AD a, |
|||||||||
AB b, AS c . Выразить MN через a, b, c |
(рис. 3.21). |
|||||||||||||
Пусть |
SM |
m , тогда |
MC |
1 m . Пусть |
DN |
n , тогда |
||||||||
NB 1 n . |
SC |
|
|
|
|
SC |
|
|
|
|
DB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разложим MN |
следующим образом: |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||
|
MN |
m (a b |
c) c |
(1 n) a n |
b |
|
|
|||||||
|
ma mb |
mc c a na nb |
|
|
(20) |
|||||||||
|
(1 n m) a |
(n m) b (m 1) c. |
|
|
||||||||||
Используя третье основное векторное соотношение, имеем: |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
AN AD |
AB AM a |
b m |
(a b c) |
|||||||||||
( m) a |
( m) b |
m c, 1. |
|
|||||||||||
Вектор AN можно разложить и по-другому: |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AN |
(1 n) a n b. |
|
|
|
|
||||||
103
