Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Балтийский федеральный университет им. И.Канта

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Попов - весь практикум по геометрии

.pdf

Скачиваний:

179

Добавлен:

10.02.2015

Размер:

16.05 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1914 15 16 17 18 19 > Следующая >>>

Глава II

Т — середины этих ребер. Найдите угол между прямой СВ1 и плоскостью , проходящей через вершину С1, параллельно прямым PQ и В1Т.

2.65. Высота МО правильной пирамиды МАВС равна стороне ее основания. На отрезке ОВ взята точка Р — середина этого отрезка. Найдите угол, который образует с плоскостью МАВ прямая МК, где К середина ребра АС.

2.66. На ребрах АВ, АС, МВ и МС правильной пирамиды МАВС все плоские углы при вершине М которой прямые, взяты соответственно точки D, Е, F и К — середины этих ребер. Точка О — точка пересечения медиан основания пирамиды. Найдите углы между следующими прямыми: 1) ВЕ и МD; 2) ВЕ и АF; 3) AF и ОК.

2.67. Высота МО пирамиды МАВСD проектируется в точку пересечения диагоналей основания, которым является прямоугольник с отношением сторон АВ: АD = 1:2, и МО= AD. На ребре МС взята точка К — середина этого ребра. Найдите углы, которые образует плоскость ВDK со следующими плоскостями: 1) АВС; 2) МСD; 3) МВС.

§ 3.1. Первое основное векторное соотношение

Глава III

РЕШЕНИЕ СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ

СПОМОЩЬЮ ОСНОВНЫХ ВЕКТОРНЫХ СООТНОШЕНИЙ

Свведением в курсе аналитической геометрии элементов векторной алгебры стало возможным применять этот аппарат к решению многих геометрических задач на вычисление. Векторный метод решения геометрических задач имеет много преимуществ, одно из которых состоит в том, что значительно упрощаются решения геометрических задач в сравнении с решениями, выполненными традиционными методами. Кроме того, векторный метод позволяет сравнительно легко делать иногда очень далеко идущие обобщения [4].

§3.1. Первое основное векторное соотношение

Определение. Будем говорить, что точка С делит отрезок АВ в отношении , если

	АС СВ.	(1)
Если	>0, то точка C делит отрезок внутренним образом,	т. е.
С АВ	, а если <0, то точка C делит отрезок внешним образом, т. е.

Слежит вне отрезка АВ.

Теорема 1. Для того чтобы точка С делила отрезок АВ в отношении , необходимо и достаточно, чтобы для произвольной точки O пространства выполнялось равенство

		1
ОС			ОА		ОВ.	(2)
ОС	1		ОА	1	ОВ.	(2)
	1			1

○ Пусть точка С делит отрезок в отношении λ, т. е. выполняется соотношение (1). Используя правило вычитания векторов, запишем ра-

венство (1) в виде

ОС	ОА (ОВ ОС)				(1 )ОС		ОА ОВ
			1
	ОС			ОА		ОВ
		1			1

Глава III

В частности, если m : n , т. е. АС : СВ m : n , то формула (2) примет вид

			n
ОС			n
ОС		m n
		m n
k		n		, 1
k	m n			, 1
	m n

		m
	OA
	OA	m n
		m n
	k	m
	k	m n
		m n


OB ОС		кОА (1	к)ОВ,

Отметим, что если точка М является серединой отрезка АВ , т. е. точка М делит отрезок АВ в отношении 1, то формула (2) примет в этом случае вид

	1		1
ОМ	2	ОА	2	ОВ.	(3)
	2		2

Формулу (3) назовем в дальнейшем формулой для середины отрезка.

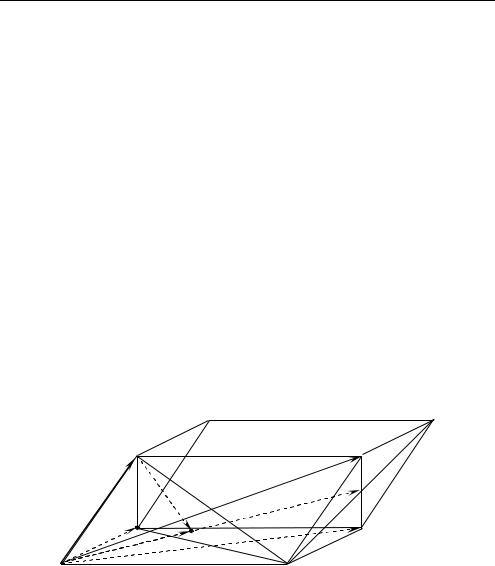
Задача 3 . 1 . Дан параллелепипед ABCDA1B1C1D1. Через вершину A к центру симметрии M грани BCC1B1 проведена прямая, пересекающая плоскость A1BD в точке N. Вычислить отношение

AN : NM (рис. 3.1).

D1	C1
A1	B1
A1

Рис. 3.1

○ 1. Пусть p,q, r — тройка некомпланарных векторов (рис. 3.1).

Разложим векторы AN

и AM

по векторам p,q, r

а) AB1

r p;

AC p q. По свойству середины M отрезка B1C (3)

AB1

p q p

§ 3.1. Первое основное векторное соотношение

b) Векторы A1D, A1N, A1B — компланарны. Тогда по признаку

компланарности векторов имеем

	A1N x A1D y A1B.
2.	Точки A, N, M лежат на одной прямой. Значит, векторы
AM	компланарны, т. е.

	AN kAM.
Подставляя (1), (2) в соотношение (3), находим
			1		1
	yp xq (1 x y)r	k p	2	q	2	r .
			2		2

AN и

(3)

(4)

Так как разложение вектора по базису p,q, r однозначно, то из (4)

следует (приравниваем коэффициенты в левой и правой частях при векторах p,q, r ):

1 x y

Из (3)

тогда

2AN AM 2AN AN NM,

т. е. AN : NM 1:1.

Ответ: AN : NM 1:1.

Задача

3 . 2 .

Плоскость

отсекает

от

боковых ребер

SA, SB ,

правильной четырехугольной пирамиды SABD ,

отрезки SK

SA , SL

SB, SM

1 SC . Какую часть ребра SD ,

считая от вершины, отсекает плоскость ?

○ Пусть

N ,

a, SB

b, SC

c, SD

(KLM ),

d ,

SO LN O1 .

Глава III

Пирамида SАBСD — правильная, поэтому ее боковые ребра равны,

т.е. SA SB SD SC a .		Рассмотрим								равнобедренный ASC .
Наша задача: выразить вектор SO1					через SO.
По свойству медианы треугольника
1								1				1
SO 2 (SA SC)								2 a				2 c.		(4)
Векторы SO1 и SO коллинеарны, поэтому
SO1 x SO				1 x a						1 x c.				(5)
				2						2
С другой стороны, так как SO1 — биссектриса в														SKM , то по
свойству биссектрисы угла имеем
	KO	SK			2	3	a		2		1
	1					3				:			.
		SM					a		3	:	3		.
	O M	SM			1	3	a		3		3
1						3
Отсюда в силу первого		основного						векторного						соотношения из
SKM (рис. 3.2) находим
SO1 2 SM			1 SK						2 c				2 a.	(6)
3			3						9				9

Рис. 3.2

§ 3.1. Первое основное векторное соотношение

Из равенств (5), (6) следует, что

12 x 92 x 94

и тогда

									SO1				4 SO.																			(7)
													9
Рассмотрим ∆SBD . Пусть SN : SD y SN yd.
Так как SO1		является биссектрисой в ∆SLN , то по свойству биссек-
трисы
							LO				SL			1	2	a		1				.
						1									2																	(8)
						1					SN			ya					2 y													(8)
							O1 N				SN			ya					2 y
Учитывая (8), по основному векторному соотношению (1) из ∆SLN
получаем:
	SO			1			SN				2 y		SL						y					d					y		b.	(9)
	SO						SN						SL											d							b.	(9)
1			1	2 y					1	2 y							1	2 y									1 2 y
			1	2 y					1	2 y							1	2 y									1 2 y
С другой стороны, из равенства (7) и SO 1 b 1 d имеем
																		1				2					2
																						2					2
			SO1			4		SO		4		( 1 b			1 d )						2		b			2		d .				(10)
			SO1					SO		9		( 1 b			1 d )								b					d .				(10)
					9					9		2			2					9					9
Из (9) и (10) следует, что:
	y			2	9 y 2 4 y y															2					SN					2 SD .
1 2 y				9	9 y 2 4 y y															5					SN					2 SD .
1 2 y				9																5										5

Ответ: 52 SD.●

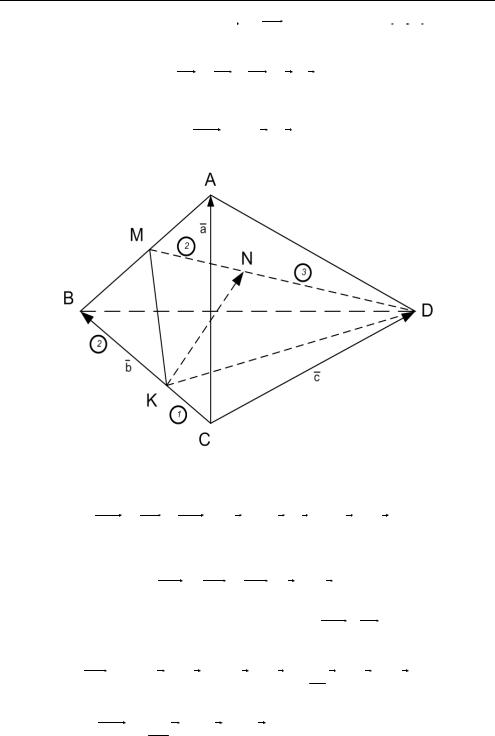
Задача 3 . 3 . АВСD — треугольная пирамида. М — середи-
на ребра AB . Точка K лежит на ребре BC , причем BK 2KC . Раз-

ложить вектор KN	по векторам a CA, b CB, c CD , если

M: N 2 : 3 (рис. 3.3).

По первому основному векторному соотношению имеем

KN	3	KM	2	KD .	(11)
	5		5

Глава III

Теперь разложим векторы KM и KD по векторам a, b, c . По правилу вычитания векторов:

BA CA CB a b.

Отсюда, учитывая, что М — середина отрезка ВА , находим

BM 12 (a b).

	Рис. 3.3
Теперь по правилу треугольника сложения векторов
2		1	1	1	(12)
KM KB BM		b 2 (a b)	2 a	3 b.
	3

Наконец,

	1	(13)
KD CD CK c	3 b.

Подставив разложения (12), (13) векторов KM , KD в формулу (11), окончательно получим:

KN 53 (12 a 13b) 52 (c 13b) 103 a 13b 52 c.

Ответ: KN 103 a 13 b 52 c . ●

§3.1. Первое основное векторное соотношение

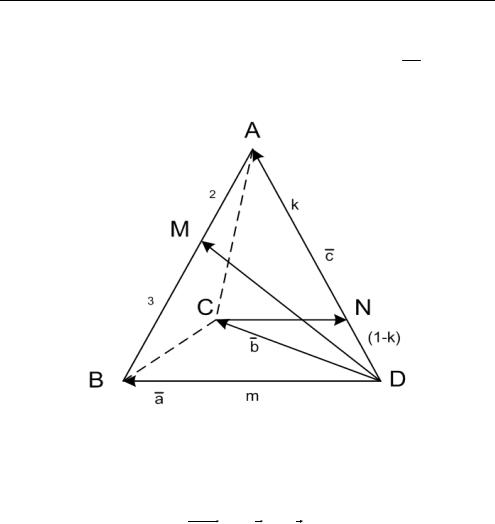
Задача 3 . 4 . Дан правильный тетраэдр АВСD с длиной ре-

бер m . M АВ, N AD ; BM : MA 2: 3, DM CN 20 m2 . В ка-

ком отношении N делит AD ? (рис. 3.4).

																Рис. 3.4
	Пусть						AN : AD k ,								тогда ND : AD 1 k .
Введем							a, b, c			— аффинный базис, тогда
															DM			2		a		3 c ,
															DM					a		3 c ,
																5						5
																			k
						CN		k CD				(1 k ) CA							k			b (1 k )( b		c)
						( k 1 k ) b									(1 k ) c						(2k 1) b (1 k ) c,
									(		2				3
						DM		CN	(		5		a		5	c) ((2k 1) b							(1 k) c)
			2								5		2		5						2			3 (1 k) m2
			2		(2k 1) m2								2	(1 k) m2							2		(2k 1) m2
	5				(2k 1) m2							5 2		(1 k) m2							5 2		(2k 1) m2
	5		2									5 2									5 2			5
		(		1		2k 1			1		1		k		3	k	3		3			3	k) m2 (1 k		3	)	m2 .
		(		5		2k 1			5		5		k		5	k			3			5	k) m2 (1 k			)	m2 .
				5				5	5		5				5	10			5			5	5	10

Глава III

По условию DM CN 207 m 2 , значит,

15 k 103 207 4k 6 7 k 14 AN : ND 1 : 3,

1 k 1 14 34 .

Ответ: AN : ND 1 : 3.

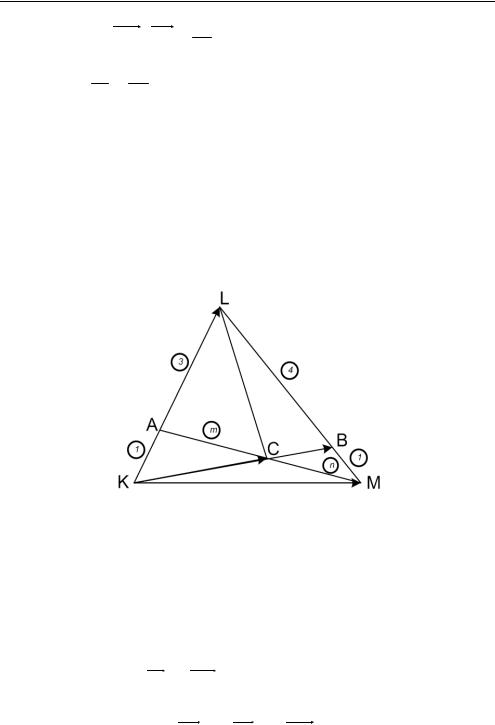
Задача 3 . 5 . В треугольнике KLM на стороне KL взята точка A так, что KA : AL = 1 : 3, на стороне LM взята точка B так, что LB : BM = 4 : 1. Пусть С — точка пересечения прямых KB и MA. Площадь треугольника KLC равна 2. Найти площадь треугольника

KLM (рис. 3.5).

		Рис. 3.5	4 S , так как у треугольников
Пусть	S KLM	S , тогда S KLB	4 S , так как у треугольников
			5

KLM и KLB одинаковая высота, которая проведена соответственно к основаниям LM и LB, где

54 LM LB.

Введем векторы KL и KM . В силу первого векторного соотношения получим

KB 15 KL 54 KM .

§ 3.1. Первое основное векторное соотношение

Пусть KС х KB , где x 0,1 , тогда

KM .

(14)

Пусть

АС

m : n ,

тогда из AKM

по первому основному

векторному соотношения получим

(15)

KC m n KA m n KM m n 4 KL m n KM .

В силу единственности разложения вектора по двум неколлинеар-

ным векторам из (14) и (15) получаем следующую систему:

n m

4(m n)

m n

;

m n

Так как KLB

и KLC имеют общую высоту, то

S KLC S KLB

4 S

S KLM

2 S KLC

2 2 4.

Ответ: S K L M

Задача 3.6. Дан куб ABCDA1B1C1D1 с ребром, равным a . На прямой AC взята точка E , такая, что AE : AC 2 : 1 , причем точка C лежит между точкамиA и E , а на прямой AB1 взяты точки O и F такие, что AO OB1 B1F . Найти расстояние между точками O и E

(рис. 3.6).

OFAO 12 . Введем декартов базис a, b, c , как указано на

рисунке (3.6).

Пусть

a, AD

b, AA1

2 AC

2(a b),

EA AF 2(a b)

(a c)

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1914 15 16 17 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.12.201834.55 Кб5Полулях, психология.docx
#
10.02.201531.31 Кб7помощь на защите 1.docx
#
10.02.201561.95 Кб33Понятие об общении коммуникативные умения (1).doc
#
02.09.2019117.93 Кб1попа.docx
#
20.09.201969.63 Кб3ПОПД.doc
#
10.02.201516.05 Mб179Попов - весь практикум по геометрии.pdf
#
10.02.20157.78 Mб100Попов - все лекции по геометрии.pdf
#
10.02.2015152.58 Кб68Портфолио к экзамену Дошк пед.doc
#
10.02.20151.95 Mб105портфолио ученика.doc
#
10.02.201514.08 Кб17Пословицы и поговорки.docx
#
17.08.20194.52 Mб81Пособие 2 студентам по ХТ.doc