Основные понятия

Случайной называют величину, которая в результате испытания принимает одно и только одно из своих возможных значений, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Другими словами, принятие случайной величиной каждого своего возможного значения  случайное событие.

Случайные величины подразделяются на два класса  дискретные и непрерывные.

Случайная величина называется дискретной, если все ее возможные значения можно изобразить изолированными точками числовой прямой.

Примеры дискретных случайных величин:

1. количество очков, выпавших на верхней грани игрального кубика при его однократном подбрасывании;

2. количество опечаток на странице рукописи;

3. число претендентов на вакантную должность;

4. число зерен в колоске злака.

Случайная величина называется непрерывной, если все ее возможные значения сплошь заполняют некоторый промежуток числовой прямой.

Примеры непрерывных случайных величин:

1. процент жира в молоке;

2. количество осадков, выпадающих в некоторой местности за некоторый месяц;

3. время ожидания автобуса на остановке.

Случайные величины принято обозначать прописными буквами конца латинского алфавита  а их возможные значения  соответственными строчными буквами с нижними числовыми индексами в случае дискретных случайных величин и без индексов – в случае непрерывных случайных величин. Так, например, возможные значения некоторой дискретной случайной величины , а – возможные значения некоторой непрерывной случайной величины . Запись означает вероятность того, что случайная величина приняла значение . Коротко эту вероятность обозначают через : . Аналогично,  вероятность того, что случайная величина приняла значение и т.д.

Соответствие между всеми возможными значениями случайной величины и их вероятностями называют законом распределения случайной величины (распределением вероятностей случайной величины). Для дискретной случайной величины закон распределения задается в виде таблицы

				…
				…		,

где .

Этот способ задания дискретной случайной величины часто называют рядом распределения. Ряд распределения дискретной случайной величины может быть представлен геометрически в виде многоугольника распределения (рис. 5.1).

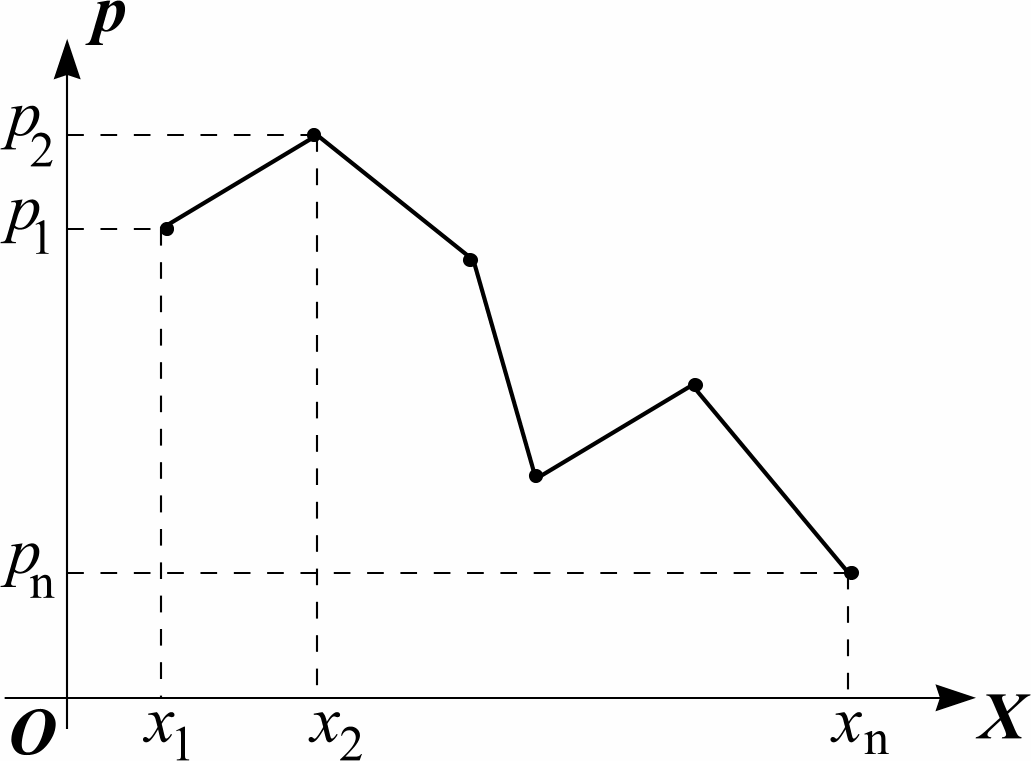
Рис. 5.1. Многоугольник распределения

Пример 5.1. Пусть число выпадений герба при бросании двух монет. Составить закон распределения случайной величины .

Решение. Случайная величина может принимать, очевидно, значения 0, 1, 2. Обозначим соответствующие им вероятности через и рассмотрим события:

{обе цифры, т.е. герб не выпал ни разу};

{герб-цифра или цифра-герб, т.е. герб выпал один раз};

{оба герба, т.е. герб выпал два раза}.

Тогда:

Таким образом, получаем искомый закон распределения

		0	1	2
		1/4	1/2	1/4	.

Очевидно, .

Пример 5.2. Стрелок, имея 4 патрона, стреляет до первого попадания в цель. Вероятность попадания при каждом выстреле постоянна и равна 0,6. Построить закон распределения числа использованных патронов.

Решение. Заметим, что стрелок использует -й патрон, если -й и все предыдущие выстрелы закончились промахами.

Введем в рассмотрение случайную величину число использованных патронов  и случайные события

{попадание в цель при первом выстреле};

{промах при первом выстреле и попадание при втором};

{промахи при двух первых выстрелах и попадание при третьем};

{промах при первых трех выстрелах}.

Очевидно, вероятность промаха при одном выстреле равна 10,6=0,4. Применяя теорему умножения вероятностей для независимых событий, получаем

Отсюда следует, что искомый закон распределения случайной величины имеет вид

		1	2	3	4
		0,6	0,24	0,096	0,064	.

Заметим еще раз, что сумма вероятностей в нижней строке таблицы равна единице.

Математическим ожиданием (средним ожидаемым значением) дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие им вероятности

Отметим следующие свойства .

1.

2.

3.

4. являются независимыми случайными величинами (это означает, что закон распределения одной из них не меняется от того, какие возможные значения приняла другая).

Разность называется отклонением случайной величины от ее математического ожидания. Отметим, что .

Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания

Для вычисления дисперсии дискретной случайной величины можно пользоваться одной из двух формул:

где , или так называемой универсальной формулой

то есть

Выделим следующие свойства :

1.

2. .

3. являются независимыми случайными величинами.

Наряду с математическим ожиданием дисперсия является важнейшей числовой характеристикой случайной величины. Она характеризует разброс, рассеяние значений случайной величины относительно ее математического ожидания. Однако дисперсия имеет одно не совсем удобное качество: ее размерность равна размерности квадрата случайной величины. Поэтому в качестве показателя рассеяния значений случайной величины относительно ее математического ожидания рассматривают чаще среднее квадратичное отклонение случайной величины (с.к.о.)

Эта величина имеет ту же размерность, что и случайная величина .

Пример 5.3. Заданы законы распределения двух независимых случайных величин :

	-4	2	6	8			1	3
	0,2	0,1	0,3	0,4			0,2	0,8

Найти математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины Z = 3X  5Y.

Решение. 1. Найдем математические ожидания случайных величин :

;

2. Получим законы распределения случайных величин :

	16	4	36	64			1	9
	0,2	0,1	0,3	0,4			0,2	0,8

3. Найдем математические ожидания случайных величин и :

;

.

4. Найдем дисперсии случайных величин и с помощью универсальной формулы:

;

5. Пользуясь свойствами математического ожидания и дисперсии, а также независимостью случайных величин и , окончательно получим:

;

6. Найдем среднее квадратичное отклонение случайной величины Z

Для непрерывных случайных величин закон распределения вероятностей, очевидно, не может быть задан в виде таблицы подобно тому, как это было сделано для дискретной случайной величины, так как нельзя перечислить все ее возможные значения в силу их структурных особенностей (кроме того, вероятность каждого отдельного значения непрерывной случайной величины равна нулю).

Представление о распределении вероятностей непрерывной случайной величины получают с помощью функции распределения либо плотности распределения вероятностей.

Функцией распределения вероятностей (интегральным законом распределения) непрерывной случайной величины называется непрерывная функция , определяемая равенством

Отметим, что:

1.  неубывающая функция и принимает значения от 0 до 1, когда пробегает значения от ;

2. вероятность того, что принимает значения между и , вычисляется по формуле

Пример графика функции распределения вероятностей непрерывной случайной величины изображен на рис. 5.2.

Рис. 5.2. Пример графика функции распределения вероятностей

непрерывной случайной величины

З а м е ч а н и е. Функция распределения используется и как закон распределения дискретной случайной величины, представляя собой графически уже разрывную ступенчатую линию.

Пример 5.4. Два стрелка делают по одному выстрелу. Вероятности попадания в мишень равны соответственно 0,5, 0,4. Составить закон распределения числа попаданий в цель, начертить многоугольник распределения и график функции распределения.

Решение. 1. Получим ряд распределения случайной величины X. Пусть

А = {первый стрелок попал в цель};

В = {второй стрелок попал в цель};

Х – число попаданий в цель.

Вычислим вероятности того, что Х примет значения 0, 1 и 2:

;

;

Таким образом, ряд распределения случайной величины X имеет следующий вид:

Х	0	1	2
Р	0,3	0,5	0,2

2. Строим многоугольник распределения (рис. 5.3):

Рис. 5.3. Многоугольник распределения

3. Строим аналитически функцию распределения случайной величины X:

1)

2)

3) либо

4)

Итак,

4. Строим график (рис. 5.4).

Рис. 5.4. График функции распределения

Плотностью распределения вероятностей (дифференциальным законом распределения) непрерывной случайной величины называется функция , определенная равенством

Выделим следующие свойства:

1)

2. 

3. 

4. 

З а м е ч а н и я.

1. График дифференциальной функции f(x) принято называть кривой распределения.

2. Если задана кривая распределения, то по ней можно узнать, чему равна вероятность P(α < X< β). Действительно, из свойства 4 следует, что P(α < X< β) равна площади криволинейной трапеции, ограниченной кривой распределения, осью абсцисс и прямыми x = α и x = β (рис. 5.5). Свойство 2 говорит о том, что площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

Рис. 5.5. Геометрический смысл P(α < X< β)

3. Объект называется дифференциалом, или элементом вероятности, и имеет следующий геометрический смысл (рис. 5.6).

Рис. 5.6. Геометрический смысл элемента вероятности

Пример 5.5. Продолжительность жизни растений некоторого вида в определенной среде представляет собой непрерывную случайную величину . Пусть плотность распределения вероятностей имеет вид

.

1. Какова функция распределения случайной величины ?

2.Какая доля растений данного вида умирает за период 100 дней?

3.Если некоторое растение живет в течение 100 дней, то какова вероятность того, что оно проживет еще не менее 100 дней?

Решение. 1. Функция распределения вероятностей для будет выглядеть следующим образом:

2. Доля растений, которые умирают за период 100 дней, выражается вероятностью

3. Искомая в этом пункте вероятность составляет:

Таким образом, примерно 30% тех растений, которые не умирают за 100 дней, будут жить по крайней мере и следующие 100 дней.

Пример 5.6. Случайная величина x задана функцией распределения

Найти плотность вероятности , построить графики функций , и вычислить P(1 x  2).

Решение. 1. Так как , то

2. Строим графики функций и (рис. 5.7):

Рис. 5.7

3. Вычисляем искомую вероятность P(1 X  2):

Непрерывные случайные величины, как и дискретные, имеют числовые характеристики для которых сохраняются перечисленные выше свойства. Эти числовые характеристики вычисляются по следующим формулам:

или

Пример 5.7. Непрерывная случайная величина Х имеет закон распределения

Найти значение параметра А, функцию распределения вероятностей случайной величины Х, числовые характеристики М(Х), , (Х) и Р(0  Х  2).

Решение. 1. Для отыскания значения А воспользуемся свойством дифференциальной функции (х)

Получаем

т.е.

2. Функцию распределения ищем по формуле

:

1)

2)

3) ,

т.е.

3. Учитывая, что 0 х  5, вычислим М(Х):

Для нахождения дисперсии D(Х) воспользуемся универсальной формулой

Среднее квадратичное отклонение будет равно

(Х) = = .

4. Теперь воспользуемся формулой

и вычислим Р(0 X  2):

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ К ТЕМЕ 5

Задача 5.1. Две независимые случайные величины и заданы своими законами распределения.

Требуется:

а) построить многоугольник распределения случайной величины ;

б) найти аналитически функцию распределения случайной величины и построить ее график;

в) найти математическое ожидание, дисперсию и среднее квадратичное отклонение случайной величины ;

г) вычислить .

1.		-4	-2	1	3			2	6
		0,1	0,3	0,5	0,1			0,2	0,8

2.		-2	-1	1	4			2	4
		0,1	0,4	0,3	0,2			0,3	0,7

3.		-2	-1	0	3			-3	2
		0,5	0,2	0,1	0.2			0,7	0,3

4.		-6	-2	1	2			-8	-2
		0,3	0,3	0,2	0,2			0,4	0,6

5.		-4	-2	-1	3			-2	8
		0,1	0,3	0,5	0,1			0,6	0,4

6.		-2	0	1	4			1	3
		0,5	0,1	0,3	0,1			0,1	0,9

7.		-7	-5	-1	2			1	3
		0,4	0,1	0,2	0,3			0,9	0,1

8.		-1	2	4	8			-2	4
		0,2	0,5	0,2	0,1			0,2	0,8

9.		-8	-5	-2	4			3	6
		0,1	0,4	0,2	0,3			0,3	0,7

10.		-6	-2	4	6			4	7
		0,1	0,6	0,2	0,1			0,5	0,5

11.		-3	-1	2	5			1	4
		0,4	0,2	0,1	0,3			0,6	0,4

12.		-5	-2	1	3			2	5
		0,3	0,2	0,1	0,4			0,2	0,8

13.		-4	-2	2	6			-5	3
		0,1	0,5	0,3	0,1			0,8	0,2

14.		-2	-1	0	4			-2	1
		0,3	0,2	0,1	0,4			0,4	0,6

15.		-7	-5	3	4			-4	3
		0,1	0,4	0,2	0,3			0,6	0,4

16.		-2	-1	4	7			-2	3
		0,5	0,1	0,3	0,1			0,9	0,1

17.		-7	-5	2	4			2	3
		0,1	0,4	0,4	0,1			0,2	0,8

18.		-6	-2	1	3			2	5
		0,4	0,1	0,3	0,2			0,6	0,4

19.		-5	-4	2	6			-6	4
		0,3	0,3	0,1	0,3			0,8	0,2

20.		-3	-2	2	7			1	3
		0,3	0,2	0,1	0,4			0,1	0,9

21.		-4	-2	1	2			-5	4
		0,2	0,4	0,1	0,3			0,7	0,3

22.		-5	-3	-1	6			-3	2
		0,1	0,2	0,5	0,2			0,3	0,7

23.		-4	-2	4	5			-4	2
		0,2	0,4	0,1	0,3			0,4	0,6

24.		-4	0	1	4			-1	2
		0,5	0,1	0,1	0,3			0,5	0,5

25.		-6	-4	3	5			-2	5
		0,4	0,1	0,2	0,3			0,1	0,9

26.		-7	-5	1	3			2	4
		0,1	0,3	0,4	0,2			0,2	0,8

27.		-6	-4	2	3			3	5
		0,2	0,4	0,1	0,3			0,9	0,1

28.		-2	-1	2	3			-5	7
		0,3	0,3	0,1	0,3			0,7	0,3

29.		-3	-1	3	5			-4	-1
		0,4	0,2	0,1	0,3			0,8	0,2

30.		-2	-1	4	5			-3	4
		0,5	0,1	0,2	0,2			0,6	0,4

Задача 5.2. Непрерывная случайная величина задана интегральной функцией распределения вероятностей .

Требуется:

а) найти дифференциальную функцию распределения ;

б) построить графики функций и ;

в) вычислить математическое ожидание , дисперсию и среднее квадратичное отклонение ;

г) найти .

1.	2.
3.	4.
5.	6.
7.	8.
9.	10.

11.	12.
13.	14.
15.	16.
17.	18.
19.	20.

21.	22.
23.	24.
25.	26.
27.	28.
29.	30.

Задача 5.3. Непрерывная случайная величина Х задана плотностью вероятностей вида

Требуется найти значение параметра А и функцию распределения .

Вариант
1		1	10
2		5	12
3		3	12
4		6	14
5		7	15
6		3	9
7		9	16
8		2	9
9		2	14
10		1	13
11		1	12
12		- 4	7
13		- 4	8
14		- 6	6
15		- 6	5
16		4	11
17		5	11
18		3	10
19		7	14
20		5	12
21		- 11	0
22		- 12	0
23		1	12
24		2	10
25		3	12
26		3	8
27		1	5
28		2	7
29		- 2	- 1
30		- 4	- 5

КОНТРОЛЬНЫЕ ВОПРОСЫ К ТЕМЕ 5

1. Что называется случайной величиной? Дискретной случайной величиной? Непрерывной случайной величиной? Приведите примеры.

2. Что понимают под распределением вероятностей случайной величины? Как выглядит закон распределения дискретной случайной величины?

3. Что такое функция и плотность распределения вероятностей непрерывной случайной величины? Какими основными свойствами обладают эти характеристики?

4.Что называется математическим ожиданием, дисперсией, средним квадратичным отклонением случайной величины? Что они характеризуют? Как вычисляются?

5.Имеется три ящика. В первом из них находятся 7 стандартных и 3 бракованных изделия, во втором  3 стандартных и 7 бракованных, в третьем  5 стандартных и 5 бракованных. Из каждого ящика случайно берут по одному изделию. Составить закон распределения случайной величины  числа бракованных изделий среди отобранных. Найти все числовые характеристики этой случайной величины. Построить ее функцию распределения.

6.Задана функция распределения непрерывной случайной величины

Требуется:

1) найти A и плотность распределения и построить графики

2) вычислить все числовые характеристики случайной величины и найти вероятность ее попадания в промежуток (0; 1).

Тема 6.

РАВНОМЕРНОЕ И ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЯ