2.2.2 Смещенный – Отклоненный компромисс.

U образная форма, наблюдаемая в кривых тестовой MSE, оказывается результатом двух конкурирующих свойств статистических методом обучения. Ожидаемая тестовая MSE, для данного значения x0, всегда можно разложить на сумму трех величин: дисперсия (f(x0)), квадрат смещения (f^(x0)) и дисперсия ошибка epsilon.

Эта формула определяет ожидаемую тестовую MSE, и относится к среднему тестовой MSE.

2.2.3 Установка Классификации.

Предположим, что мы стремимся оценить f на основе учебных наблюдений {(x1,y1),…, (xn,yn)}, где yi является качественными переменными. Для определения количественной оценки точности оценки f^ является частота ошибок обучения, доля ошибок, которые сделаны если мы применяем оценку f к учебным наблюдениям:

yi^ - это метка предсказанного класса для ­i- ого наблюдения с использованием f^.

I(yiyi^) является переменной индикатором, равной 1, если yiyi^ и равной 0, если yi=yi^. Если I равно 0, то i-е наблюдение было классифицировано правильно метом классификации, иначе нет. => уравнение 2.8 вычисляет долю неправильных классификаций. Мы более заинтересованы коэффициентом ошибок. Он связан с набором тестовых наблюдений формы (x0,y0):

у0 – метка предсказанного класса, которая следует из применения классификатора к тестовому наблюдению с предсказателем x0. Классификатор хорош при минимальном коэффициенте ошибки.

Можно показать, что тестовый классификатор ошибок сводится к минимуму, простым классификатором который назначает каждое наблюдение на наиболее вероятный класс, учитывая его значение предсказателя. т.е. мы должны присвоить тестовое наблюдения с предсказателем вектора x0 к классу J, для которого:

является самым большим. 2.10 – это условная вероятность: вероятность того, что Y=j, учитывая наблюдаемый вектор предсказателя х. Это классификатор Байеса. В задаче с двумя классами, где есть только возможные значения ответа, предсказать, что класс 1 или 2, классификатор Байеса прогнозирует класс 1, если Pr(Y = 1|X = x0) > 0.5 и второй иначе.

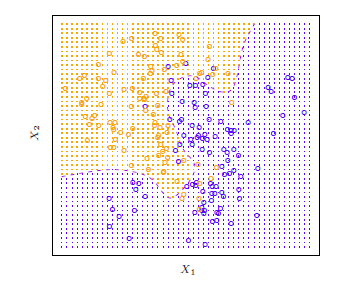
рис 2.13

Этот рисунок показывает использование моделируемого набора данных в двумерном пространстве, состоящий из предикатов х1 и х2. Оранжевые и синие круги соответствуют учебным наблюдениям, которые принадлежат двум различным классам. Для каждого значения х1 и х2, существует вероятность того, что ответ может быть оранжевый или синий. т.к. это смоделированные данные, мы можем вычислить их условные вероятности. оранжевая заштрихованная область отображает множество точек, для которых Pr(Y = оранжевый|X), что больше 50%, в то время как синяя указывает на множество точек, для которых вероятность ниже 50%. Фиолетовая пунктирная линия представляет собой точки, где вероятность точно 50% - это граница решения Байеса.

Классификатор Байеса приводит минимально возможный коэффициент тестовой ошибки, это коэффициент ошибок Байса. т.к. классификатор Байса всегда будет выбирать тот класс, для которого 2.10 будет максимальна, коэффициент ошибок при х = х0 будет 1−maxj Pr(Y =j|X = x0). В целом, полный коэффициент ошибок Байеса определяется, как

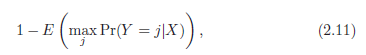
где ожидание составляет вероятность по всем возможным значениям Х. Коэффициент ошибок Байеса составляет 0,1304, для наших моделируемых данных. Коэффициент ошибок Байеса аналогичен непереводимым ошибкам.

k - Ближайших соседей. (KNN)

Дано целое положительное число К и тестовое наблюдение х0, классификатор KNN сначала определяет K точек в обучающих данных, которые ближе всего к х0, представленному N0. Затем он определяет условную вероятность для класса j как доля точек в N0, значение ответа которого равняется j:

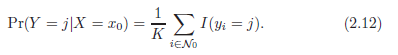
KNN применяет метод Байеса и классифицирует тестовое наблюдение x0 к классу с самой большой вероятностью.

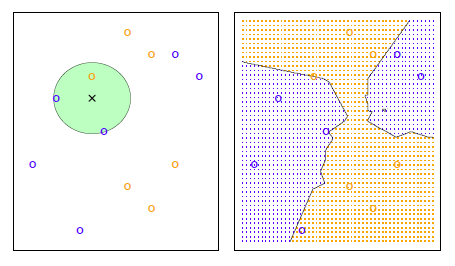
рис 2.14

Этот рисунок иллюстрирует пример подхода KNN. В левой части мы построили наибольший набор обучающих данных, состоящий из шести синих и шести оранжевых наблюдений. Цель состоит с том, чтобы сделать предсказание для точки, помещенной черным крестом.

Предположим, что мы выбираем К=3. Тогда KNN будет сначала определять три наблюдения, которые находятся ближе к кресту. Это место показано в виде круга. Он состоит из двух синих точек и одной оранжевой точки, в результате оценочных вероятностей 2/3 для синего класса и 1/3 для оранжевого класса. Следовательно, KNN предскажет, что черный крест принадлежит к синему классу. В правой панели мы применим подход KNN c K = 3 во всех возможных значениях для х1 и х2, и привлекли к соответствующей границе решения KNN.

несмотря на то, что это очень простой подход, KNN часто проводит классификации, которые близки к оптимальному классификатору Байеса.

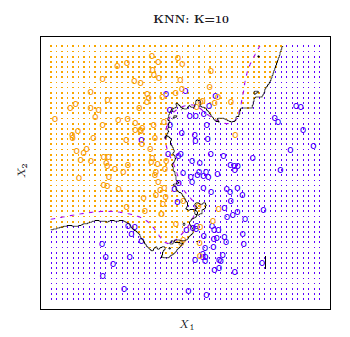
рис2.15

Рис 2.15 показывает границу решения KNN, используя к = 10, когда наносится более крупный моделируемый набор данных из рис2.13. Хоть и не известно истинное распределение классификатора KNN, граница решения KNN очень близка к классификации Байеса. Коэффициент ошибок KNN равен 0,1363, что близко к коэффициенту ошибок Байеса 0,1304.

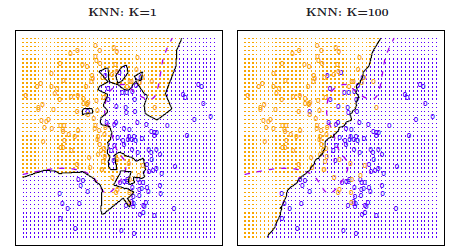
рис 2.16

Выбор К имеет сильный эффект на полученный классификатор KNN. Рис 2.16 показывает два KNN подхода для моделируемых данных из рис 2.13, используя К=1 и К=100. При К=1 граница решения чрезмерно гибка и находит закономерности в данных, которые не соответствуют границе Байеса. Это соответствует классификатору, который имеет низкое смещение, но очень высокую дисперсию. По мере роста K, метод становится менее гибким и производит границу решения, которая близка к линейной. Это соответствует низкой дисперсии, но классификаторы высокого смещения. На моделируемом наборе данных, ни К=1, ни К = 100 не дают хорошие прогнозы: они имеют тестовые коэффициенты ошибок 0,1695 и 0,1925, соответственно.

В условиях регрессии, нет прочных отношений между учебным коэффициентом ошибок и тестовым коэффициентом ошибок. С К = 1, учебный коэффициент ошибок KNN равен 0, но тестовый коэффициент ошибок может быть довольно высоким.

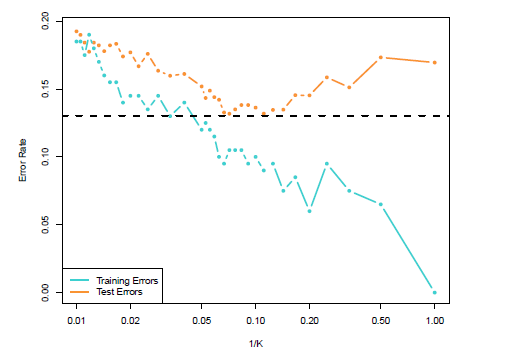
рис 2.17

На рис 2.17 нанесены тестовые и учебные ошибки KNN, функции 1. Как 1 последовательно уменьшает учебный коэффициент ошибок, когда гибкость увеличивается. Тем не менее, тестовая ошибка проявляет характерную U – образную форму, сначала уменьшаясь доследующего увеличения, когда метод становится чрезмерно гибким.

И в регрессии и в настройках классификации, выбор правильного уровня гибкости имеет решающее значение для успеха любого статистического метода обучения. Компромисс дисперсии-смещения, и получение в результате U-образную форму в тестовой ошибке, может сделать это трудной задачей.