2.1.2. Как оценить f?
Мы всегда будем считать, что мы рассматриваем множество n различных точек данных. Например на рисунке 2.2 мы наблюдали 30 точек данных. Эти наблюдения называются данными обучения, потому что мы будем использовать эти наблюдения для тренировки, для обучения метода оценки f. Пусть Xij представляет значение j-ого предсказателя или вход, для наблюдения i, где i = 1,2,3,...,n и j=1,2,3,...,p. Соответственно, пусть Yi представляет собой переменную ответ на i-е наблюдение. Тогда наши учебные данные состоят из {(x1,y1), ... , (xn,yn)}, где xi = (xi1, ... , xip)^T.
Мы хотим найти такую функцию f, что Y f(X) для любого наблюдения (Х,У). Большинство статических методов обучения для этой задачи можно характеризовать либо параметрический, либо непараметрический метод.
Параметрические методы
Такие методы включают два этапа:
Мы делаем предположение о функциональной форме, или форме f. Например, предположение, что f линейна на Х:
После того как мы предположили, что f является линейной функцией, задача оценки f упрощена. Вместо того, чтобы оценивать полностью произвольную p-мерную функцию f(X), необходимо лишь оценить p+1 коэффициент 0, 1, ..., p.
Как выбрана модель, нам нужна процедура, которая использует учебные данные, чтобы соответствовать 0, 1, ..., p. То есть, нам необходимо найти значения этих параметров таких, что:
Наиболее распространенный подход к подгонке модели (2.4) называется методом Наименьших квадратов, это способ оценки линейной модели.
Этот подход есть параметрический. Это уменьшает проблему оценки f до одного из оценки набора параметров. Выбор параметрической формы для f – упрощает проблему оценки f, потому что гораздо легче оценить набор параметров, как 0, 1, ..., p. в линейной модели 2.4, чем для произвольной функции f. Недостаток: модель, которую мы выбираем, не совпадает с истинной формой f. Если выбранная модель слишком далека от истинного f, то наша оценка будет плохой. Эту проблему можно решить, выбрав гибкую модель, которая более может соответствовать различным возможным функциональным формам f. но в целом, подгонка более гибкой модели требует оценки большого количества параметров. Эти более сложные модели могут привести к подгонке данных, которая по существу означает, что они приводят к ошибкам.
Рассмотрим рисунок 2.4, показывающий пример параметрического подхода применительно к данным о доходах рис 2.3.
рис 2.4
У нас есть линейная модель вида:
доход ≈ β0 + β1 × образование + β2 × стаж.
Т.к. мы предположили линейную зависимость между ответом и двумя предикторами, вся проблема подгонки сводится к оценке 0, 1, ..., p, которые мы оценим с помощью метода наименьших квадратов линейной регрессии. Сравнивая 2.3 и 2.4, мы видим, что линейное соответствие (подгонка) на рисунке 2.4 не совсем правильно. Тем не менее, линейная подгонка все еще делает серьезную работу по завоеванию положительной взаимосвязи между годами образования и доходами, а также менее положительную взаимосвязь между стажем и доходами. Вполне возможно, что при таком небольшом количестве наблюдений, это лучшее, что мы можем сделать.
Непараметрические методы
Такие методы стремятся оценить f, которая получается как можно ближе к точкам данных, не будучи слишком грубым или волнистым (приблизительным). Такие подходы избегая предположение о конкретной функциональной форме для f, имеют потенциал, чтобы точнее соответствовать более широкому диапазону возможных форм для f.
Непараметрические подходы могут полностью избежать опасности того, что функциональная форма, использующаяся для оценки f, сильно отличается от истинного f, т.к. никакое предположение о виде f не производится. Основной недостаток: т.к. такие методы не могут свести задачу оценки f для небольшого числа параметров, очень большое число наблюдений требуется для того чтобы получить точную оценку для f.
Пример непараметрического подхода к подгонке данных о доходах представлен на рисунке 2.5.
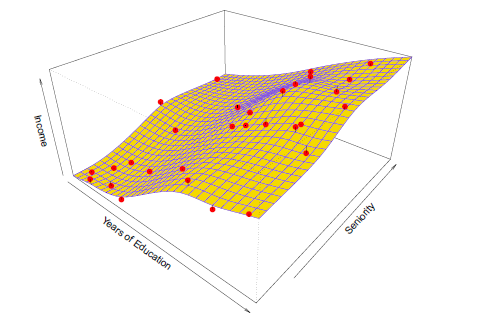
рис 2.5
Тонкая платина используется для оценки f. Этот подход не предполагает никакой заранее заданной модели f. Вместо попытки получить оценку f, которая максимально близка к наблюдаемым данным, при условии f – желтая поверхность на рисунке 2.5 – гладкая. В этом случае, непараметрический метод произвел точную оценку истинной f, показанной на рисунке 2.3. Для того чтобы соответствовать сплайну тонкой пластины, необходимо выбрать уровень гладкости. Рис 2.6. показывает ту же самую подгонку сплайна тонкой пластины, используя более низкий уровень гладкости, что позволяет более грубую подгонку.
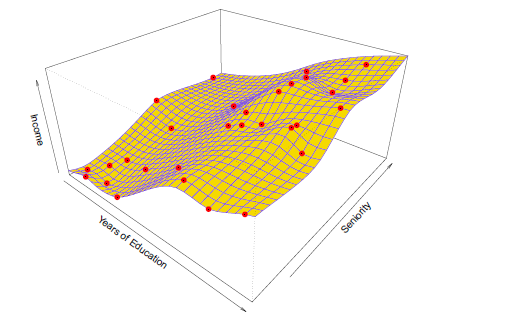
Рис 2.6
Итоговая оценка соответствует наблюдаемым данным. Тем не менее, подгонка сплайна, показанная на рисунке 2.6, является гораздо более изменчивой, чем истинная функция f на рисунке 2.3. Это нежелательно, потому что полученная подгонка не приведет к точным оценкам ответа на новых наблюдениях, которые не были частью первоначального набора данных обучения.