
Проверка_стат._гипотез,_май_2011
.pdfДружининская И.М.
Решение задач математической статистики
по теме
«Проверка статистических гипотез»
Учебное пособие для студентов экономических факультетов
Москва - 2011
1
Аннотация
Цель пособия – показать, как следует решать некоторые типы задач
математической статистики по проверке статистических гипотез. Подробный анализ процедуры решения примеров поможет студентам более глубоко разобраться в этом важном разделе математической статистики. Целесообразно напомнить, что методы проверки различных статистических гипотез широко используются в настоящее время аналитиками для получения обоснованных выводов при анализе практически значимых проблем экономической и социологической направленности,
В пособии не дается подробное теоретическое обоснование приемов решения задач, приведено лишь краткое теоретическое введение в тему и перед каждым рассмотренным типом задач дана компактная сводка используемых формул.
В пособии подобраны задачи экономической и социологической тематики. В
частности, формулировки некоторых задач предложены студентами факультета менеджмента Национального исследовательского университета - Высшая школа экономики (ВШЭ), на котором автор пособия в течение ряда лет читал курсы по теории вероятностей и математической статистике. Данное пособие будет полезно студентам,
изучающим математическую статистику на экономических, социологических и психологических факультетах вузов, в частности, при подготовке к выполнению домашних заданий, контрольных и курсовых работ.
В написании пособия творческое участие принял доцент кафедры высшей математики ВШЭ, канд.физ.-мат. наук Матвеев В.Ф., за что автор ему весьма признателен.
2
Содержание |
стр. |
1. Краткое обоснование алгоритма решения задач по проверке
статистических гипотез (теоретическое введение)……………………………4
2.Проверка гипотезы о числовом значении математического ожидания (о числовом значении генеральной средней)
нормально распределенной генеральной совокупности……………………..9
3.Проверка гипотезы о числовом назначении вероятности биноминального закона распределения (о числовом
значении генеральной доли)……………...……………………………………..18
4.Проверка гипотезы о равенстве математических ожиданий
(о равенстве генеральных средних) двух нормально распределенных генеральных совокупностей…………………………………27
5.Проверка гипотезы о равенстве вероятностей биномиального закона распределения (о равенстве долей
признака) двух генеральных совокупностей…………………………………...31
6.Проверка гипотезы о значимости выборочного коэффициента корреляции Пирсона……………………………………………………………..34
7.Проверка гипотезы о значимости выборочного коэффициента корреляции Спирмена…………………………………………………………...39
8.Критерий знаков………………………………………………………………….43
Приложение:
Таблица «Значения интеграла вероятностей»….………………………………57
Таблица «Критические точки распределения Стьюдента»…...………………58
Таблица «Критические точки распределения χ2 (или
распределения Пирсона)»…………………………...…...……………...………59
Список литературы………………………….….………………….…………….60
3
1. Краткое обоснование алгоритма решения задач по проверке
статистических гипотез
(теоретическое введение)
Статистической называют гипотезу о виде неизвестного распределения или о
параметрах изучаемого признака.
Примеры статистических гипотез:
1.Математическое ожидание изучаемого нормально распределенного признака в генеральной совокупности равно 100 кг.
2.Вероятность данного события равна 0.6.
3.Изучаемый признак в генеральной совокупности имеет показательный закон распределения.
4.Уровень производственного брака в данной партии товара ниже 0.05%.
Постановка задачи начинается с выдвижения основного утверждения (нулевой или основной гипотезы Н0), причем наряду с выдвинутой гипотезой всегда рассматривают и противоречащую ей гипотезу, которую называют конкурирующей или альтернативной гипотезой Н1.
Примеры: |
1) Н0: р=0.7; |
2) Н0: m=3; |
|
Н1: р≠0.7 . |
Н1: m>3. |
|
Здесь р – вероятность; |
m – математическое ожидание. |
Далее на основе экспериментальной информации конструируется специально подобранная из разумных соображений случайная величина, являющаяся функцией от результатов наблюдений, распределение которой известно при выполнении гипотезы
Н0. Именно эта случайная величина K, которую называют статистическим критерием или просто критерием служит для проверки справедливости нулевой гипотезы Н0.
После выбора определенного критерия K множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза принимается на фоне сопутствующей
4
конкурирующей гипотезы, а другое, при которых нулевая гипотеза отвергается,
позволяя считать утверждение, высказанное в конкурирующей гипотезе, обоснованным.
Областью принятия гипотезы (областью допустимых значений критерия)
называют совокупность значений критерия, при которых нулевую гипотезу принимают.
Это такие значения критерия, которые характерны для известного при справедливости нулевой гипотезы распределения критерия K. Характерными или естественными будем называть значения критерия, которые характеризуются большой вероятностью появления. Величину этой вероятности обсудим ниже.
Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают в пользу конкурирующей гипотезы. Это такие значения критерия, которые не характерны для данного распределения, т.е. возникающие с малой вероятностью для этого распределения.
Критическими точками (границами упомянутых областей) Kкр называют точки,
отделяющие критическую область от области принятия гипотезы.
Гипотеза называется параметрической, если речь идет об утверждении,
связанном с каким-то конкретным параметром. В противном случае она называется непараметрической.
Гипотеза называется простой, если речь идет о том, что неизвестный параметр принимает какое-то конкретное значение. Если речь идет о многих значениях параметра, то она называется сложной (см. вышеприведенные примеры: -
это пример простой гипотезы; Н1: m>3 – это пример сложной гипотезы).
Процедура проверки простой параметрической гипотезы выглядит так:
1.Формируют нулевую гипотезу Н0 и альтернативную гипотезу Н1 на основе выборочных данных.
2.Конструируют, исходя из логики задачи, случайную величину на основе результатов выборки, которую в данном разделе называют критерием; распределение
критерия в случае истинности гипотезы Н0 должно быть известно.
5
3. Вся область возможных значений критерия разбивается на две подобласти (или два подмножества).
Одно подмножество – это совокупность естественных (правдоподобных), т.е.
наиболее вероятных для данного распределения значений. В это подмножество критерий попадает с высокой вероятностью . Эта вероятность задается в условиях
задачи. Она носит название «доверительная вероятность» (иначе «уровень доверия»).
Обычно для задают следующие стандартные значения: = 0.90; 0.95; 0.99. Если
значение доверительной вероятности взять равным 1, то в этом случае область естественных значений параметра становится бесконечно большой, при этом алгоритм проверки статистической гипотезы разрушается.
Другое подмножество – это область редко возникающих для данного закона
распределения (неправдоподобных) значений критерия, которые однако характерны
для значений критерия, если справедливой является конкурирующая гипотеза.
Вероятность попадания критерия K в эту область мала и равна = 1- ; носит название «уровень значимости». Для задают такие стандартные значения:
= 0.10; 0.05; 0.01; понятно, что достаточно задать либо значение доверительной вероятности, либо значение уровня значимости. Критерий K принято обозначать через t.
4.На основе выборочных значений изучаемого признака вычисляют значение
критерия (или tнабл ). Его называют «наблюдаемое значение критерия»; при критерии стоит индекс «набл». Если значение Kнабл попадает в область правдоподобных значений для данного закона распределения, то с вероятностью утверждают, что гипотеза Н0 не противоречит экспериментальным данным на фоне конкурирующей гипотезы, а поэтому принимают именно основную гипотезу. Если значение попадает в область неправдоподобных для данного закона распределения значений, то гипотезу Н0 отвергают и принимают, следовательно, альтернативную гипотезу Н1 .
5.Если при проверке гипотезы Н0 эта нулевая гипотеза принимается, то данный факт
не означает, что высказанное в нулевой гипотезе утверждение является единственно
верным. Просто утверждение нулевой гипотезы не противоречит имеющимся
6
выборочным данным. Возможно, что и другое утверждение также не будет противоречить выборочным данным.
6. Не вдаваясь в более сложные и тонкие утверждения, связанные с принятием нулевой гипотезы или же альтернативной гипотезы, отметим лишь следующее. Если наблюдаемое значение критерия Kнабл попадает в область неестественных значений и мы, следовательно, отвергаем гипотезу Н0 и принимаем гипотезу Н1, то не можем ли мы при этом совершить ошибку - отвергнуть верную гипотезу Н0 и принять ложную гипотезу Н1? Да, можем, но вероятность этой ошибки мала. В связи со сказанным отметим смысл ранее введенного понятия уровня значимости – это вероятность отклонить нулевую гипотезу в пользу альтернативной гипотезы при условии, что в действительности верна нулевая гипотеза (иначе: Р (Н1/ Н0) = ).
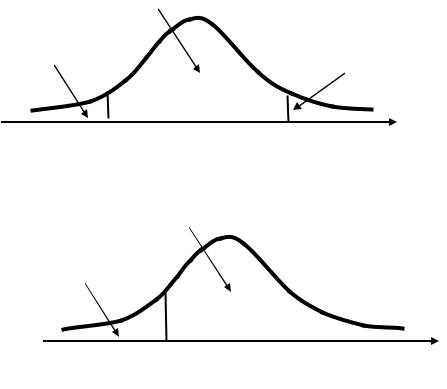
Вид альтернативной гипотезы
(для исходной простой параметрической гипотезы Н0 : = 0) может быть таким:
1. Н1: ≠ 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
+ =1 |
|
|
|
|
|
|
|
|
|
|
|
/2 |
|
|
|
|
|
|
|
|
|
/2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Двусторонняя критическая область |
К |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Н1: < 0 |
|
|
|
|
|
|
+ =1 |
|
|
|
|
|
|
|
Левосторонняя критическая область |
К |
||||
7
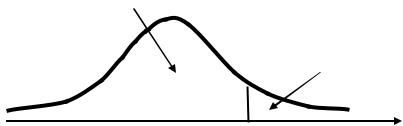
3. Н1: > 0 |
|
|
|
|
|
|
|
|
|
|
|
+ =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правосторонняя критическая область |
К |
Как ясно из приведенных выше графиков вид альтернативной гипотезы рождает ту или иную конфигурацию критической области (двустороннюю, левостороннюю,
правостороннюю).
В пособии не вводятся понятия ошибок первого и второго рода, мощности критерия. Это сделано осознанно с тем, чтобы основное внимание студентов сосредоточить на реализации стратегической идеи метода, без какой-либо более глубокой и усложняющей идею метода детализации. Более подробное знакомство с теоретическим фундаментом, лежащим в основании проверок статистических гипотез,
можно осуществить с помощью, в частности, книг [1] - [6].
В пособии рассмотрены только некоторые, наиболее распространенные типы задач по проверке статистических гипотез. В литературе их можно найти неизмеримо больше. Могут быть, например, отмечены публикации [5], [7], [8], в которых рассмотрены приложения метода проверки статистических гипотез в психологических,
социологических и экономических исследованиях.
Отметим, что некоторые задачи, приведенные в пособии, были предложены и решены студентами факультета менеджмента ВШЭ в процессе изучения или курса математической статистики..
Статистические таблицы, применяемые для решения задач, даны в приложении в самом конце пособия.
Объяснения того, почему в определенных типах задач рассматриваются приведенные формулы для вычисления критерия и почему для критерия характерен указанный закон распределения, в пособии опущены. Здесь можно отослать
8

заинтересованных студентов, например, к упомянутым выше литературным источникам или ко многим другим учебникам по математической статистике. В рамках данного пособия, нацеленного на помощь студентам в решении основных, наиболее часто встречающихся типов задач по проверке статистических гипотез, перед каждым типом задач дается лишь набор готовых формул без объяснения того, как они были получены,
почему именно их следует использовать в решении.
2. Проверка гипотезы о числовом значении математического
ожидания (числовом значении генеральной средней)
нормально распределенной генеральной совокупности
Будем обозначать математическое ожидание (истинное значение параметра)
символом m, а генеральную среднюю символом x Г ; смысл этих параметров идентичен – это числовая константа, вокруг которой располагаются значения изучаемого признака в генеральной совокупности. Введение разных символов обусловлено лишь различиями в акцентах при постановке задачи, когда суть задачи более точно передается термином «математическое ожидание», а в других задачах более приемлем термин «генеральная средняя».
Постановка задачи:
Н0: m = m0;
Н1: m ≠ m0 …. (1); m< m0 или m> m0 …………..(2);
здесь m0 – заданное условием задачи число.
Вводим критерий
K = t = ( х - m0 ) •  n . S
n . S
9
В этом выражении x - среднее арифметическое, вычисленное на основе выборки
(выборочное среднее арифметическое); n - объем выборки; S - выборочное стандартное отклонение:
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
∑x |
|
|
∑(x - |
|
)2 |
|
|
||
|
|
|
|
|
х |
|
|
||||||
|
|
|
|
|
i |
|
|
i |
|
|
|
||
|
|
х = |
i=1 |
|
; |
S = |
|
i=1 |
|
|
. |
||
|
|
n |
|
|
n - 1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
1) |
Если объем выборки n мал (n≤30), то при справедливости нулевой гипотезы |
||||||||||||
можно считать, что случайная величина |
t имеет распределение Стьюдента с k = n-1 |
||||||||||||
степенями свободы. Находим |
tкр (по |
значениям k |
и |
) на основе таблицы |
|||||||||
«Критические точки |
распределения |
Стьюдента» |
(эта |
|
таблица находится в |
||||||||
Приложении), причем для альтернативной гипотезы вида (1) используем двустороннюю критическую область, а для альтернативной гипотезы вида (2) используем одностороннюю критическую область;
2) Если объем выборки n велик (n>30), то можно приближенно считать, что
случайная величина t имеет стандартный нормальный закон распределения, поэтому находим tкр по таблице интеграла вероятностей на основе решения
уравнения |
Ф (tкр ) = |
γ |
для |
альтернативной гипотезы |
вида (1) и |
||
|
|||||||
|
0 |
2 |
|
|
|
|
|
уравнения |
Ф (tкр ) = γ - 0.5 |
для |
альтернативных гипотез |
вида (2). |
|||
|
0 |
|
|
|
|
|
|
Соответствующая |
таблица |
значений |
интеграла вероятностей |
Ф0 находится в |
|||
Приложении.
3)Для повышения точности вычислений переход от одного закона распределения
(Стьюдента) к другому закону распределения (стандартному нормальному) следует делать не при объеме выборки, равном 30 (n=30), а при объеме выборки, равном 120
(n=120).
В данном пособии переход от закона Стьюдента к стандартному нормальному закону распределения будем совершать, когда объем выборки превзойдет значение 30.
10
