
Проверка_стат._гипотез,_май_2011
.pdf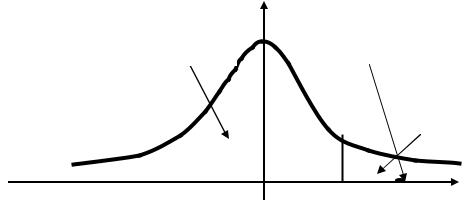
|
φ(t) |
=0.90 |
tнабл=1.86 |
|
=0.10
0 tкрп=1.28 t
График показывает, что наблюдаемое значение критерия попало в критическую область, поэтому следует сделать тот же вывод, который был получен ранее: средний рост московских и новосибирских юношей значимо отличается.
5. Проверка гипотезы о равенстве вероятностей биномиального
закона распределения (о равенстве долей признака) двух
генеральных совокупностей
Рассмотрим две генеральные совокупности.
Из первой генеральной совокупности делается случайная выборка объемом n1, и
на основе этой выборки выясняется, сколько объектов выборки обладает изучаемым признаком – этих объектов k1.
Из второй генеральной совокупности делается случайная выборка объемом n2;
количество объектов выборки, обладающих изучаемым признаком, - k2.
Выборочные доли признака по двум генеральным совокупностям равны соответственно
w1= k 1 / n1 ; w2= k 2 / n2.
31
В данном пункте мы ограничимся лишь случаем, когда выборки достаточно
большие: n1>30, n2>30.
Постановка задачи:
Н0 : p1 = p2 |
, |
|
( или |
WГ1 = WГ2 |
) |
|||||||||||
Н1 : p1 ≠ p2 |
....( или |
|
WГ1 ≠WГ2 ) ........ .........(1); |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
p1 < p2 или |
p1 > p2 .......(2) |
||||
В такой задаче в качестве критерия используется случайная величина вида |
||||||||||||||||
|
t = |
|
|
|
w1 - w2 |
|
|
|
|
|
. |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
~ |
~ |
1 |
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
p(1 - p)( |
n |
|
+ |
n |
|
) |
|
|
||||
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
||
|
~ |
|
k1 + k 2 |
|
|
|
|
|
|
|
|
|
|
|||
Здесь |
p = |
|
|
|
- |
|
наилучшая точечная оценка вероятности при |
|||||||||
n1 + n2 |
|
|||||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
справедливости нулевой гипотезы.
Если гипотеза H0 справедлива, то введенный выше критерий приближенно имеет стандартный нормальный закон распределения.
Рассмотрим пример, в котором реализуется рассмотренный выше случай..
Пример:
Перед экспертами поставлена задача оценить сравнительную активность электората Москвы и Санкт-Петербурга при избрании депутатов Государственной Думы. С этой целью была осуществлена случайная выборка в двух этих городах из состава населения, которое имеет право голоса. Было выяснено, какая часть выборки реально пришла на избирательный участок для участия в выборах. Данные оказались следующими: в Москве из 1500 потенциальных случайно выбранных избирателей реально в выборах приняли участие 480 человек, а в Санкт-Петербурге из 1630
потенциальных избирателей на избирательные участки пришли 490 человек. На уровне значимости α=10% проверить гипотезу о равенстве генеральных долей избирателей в двух этих городах, реально принявших участие в выборах.
32

Решение:
Постановка задачи:
Н0 : WГ1 = WГ2 ;
Н1 : WГ1 ≠WГ2 .
Здесь генеральные доли московских и питерских избирателей, реально принявших участие в выборах, обозначены WГ1 , WГ2 .
Экспериментальные значения:
n1 = 1500, k1 = 480; n2 = 1630, k2 = 490.
Вычислим на основе экспериментальных данных выборочные доли и точечную оценку вероятности при справедливости нулевой гипотезы:
|
|
w = |
|
k1 |
= |
|
480 |
≈0.32; w |
= |
|
k2 |
|
= |
490 |
|
≈0.30 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
1 |
|
|
|
n1 |
|
|
|
1500 |
2 |
|
|
|
n2 |
1630 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
~ |
|
k1 + k2 |
480 + 490 |
|
970 |
|
≈0.31. |
|
|
|
|
|
||||||||||||||||||||
|
|
p = |
|
|
|
|
= |
|
|
|
= |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
n + n |
2 |
1500 +1630 |
|
3130 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Вычислим на основе экспериментальных данных наблюдаемое значение |
||||||||||||||||||||||||||||||||
критерия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
t = |
|
w1 - w2 |
|
|
|
|
|
|
|
→ tнабл = |
|
|
|
|
|
|
0.32 - 0.30 |
|
|
|
|
≈1.21. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
~ ~ |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|||||||||||||
|
|
p(1 - p)( |
n |
+ |
n |
2 |
|
) |
|
|
0.31 |
• 0.69 • ( |
1500 |
+ |
1630 |
) |
|
|||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найдем границы двусторонней критической области, таблично (с помощью
функции Ф0, значения которой даны в Приложении) решив следующее уравнение:
α = 0.10 → γ = 1 - α = 1 - 0.10 = 0.90 → Ф0 (tкр ) = |
γ |
= |
0.90 |
= 0.45 => tкр = 1.65. |
|
2 |
2 |
||||
|
|
|
33
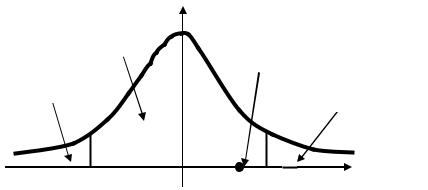
Покажем все найденные значения на графике плотности стандартного нормального закона распределения, который описывает поведение случайной величины t при справедливости нулевой гипотезы:
|
=0.90 |
φ(t) |
|
|
|
|
|
tнабл=1.21 |
/2=0.05 |
|
/2=0.05 |
|
|
tкр= -1.65 |
0 |
tкр=1.65 |
t |
Поскольку наблюдаемое значение критерия попало в область естественных для данного закона распределения значений (в данном случае стандартного нормального закона распределения), то гипотеза H0 принимается как не противоречащая экспериментальным данным с уровнем доверия 90%, т.е. генеральные доли электората,
реально принявших участие в выборах в Москве и Санкт-Петербурге, значимо не отличаются (их можно считать одинаковыми).
6. Проверка гипотезы о значимости выборочного коэффициента
корреляции Пирсона.
Рассматривается двумерная нормально распределенная генеральная совокупность (X,Y), т.е. случайные величины X и Y в ней распределены нормально. Из этой совокупности извлечена случайная выборка объемом n пар (xi , yi) и по ней вычислен выборочный коэффициент корреляции Пирсона, который оказался отличным от нуля. Возникает вопрос, объясняется ли это действительно существующей линейной связью между случайными величинами X и Y в генеральной совокупности или является следствием случайности отбора переменных в выборку. Можно ли при этом заключить,
34
что и коэффициент корреляции между случайными величинами X и Y во всей генеральной совокупности также отличен от нуля?
Напоминание:
Формула |
для вычисления линейног о |
коэффициента |
||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
||||||
|
|
|
(xi |
x |
) ( yi |
y |
) |
|
|
|
|
|||||
корреляции |
Пирсона r |
|
i 1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n |
n |
|||||||||||||||
|
|
|
||||||||||||||
|
|
|
(xi |
x |
)2 |
( yi |
y |
)2 |
|
|
||||||
|
|
|
i 1 |
i 1 |
||||||||||||
Постановка задачи:
H0: ρ=0;
H1: ρ≠0.
Если нулевая гипотеза отвергается, то это означает, что коэффициент корреляции в генеральной совокупности значимо отличается от нуля (кратно говоря
«значим»), и, следовательно, в генеральной совокупности признаки X и Y связаны линейной зависимостью. Если же принимается нулевая гипотеза, то следует считать,
что генеральный коэффициент корреляции незначим, и, следовательно, признаки X и Y
вгенеральной совокупности не связаны линейной зависимостью.
Вкачестве критерия проверки нулевой гипотезы используется случайная
величина
t = r • 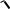
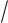 n - 2
n - 2 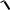
 1 - r 2
1 - r 2
Показано, что эта случайная величина (критерий) при справедливости нулевой гипотезы имеет распределение Стьюдента с k = n - 2 степенями свободы. Число степеней свободы на две единицы меньше объема выборки, поскольку в выражении для r задействованы две связи, заданные формулами для вычисления средних значений по выборке:
35

|
n |
|
|
n |
|
|
∑xi |
|
|
∑yi |
|
x = |
i=1 |
; |
y = |
i=1 |
. |
n |
|
||||
|
|
|
n |
||
Ясно также, что при больших объемах выборки (n>30) можно вместо распределения Стьюдента использовать стандартный нормальный закон распределения.
Поскольку конкурирующая гипотеза имеет вид ρ≠0, то следует строить двустороннюю критическую область.
Определив, куда попадает наблюдаемое значение критерия tнабл, делаем вывод о принятии нулевой или же альтернативной гипотезы:
если | tнабл |<tкр, то принимается гипотеза H0; если | tнабл | tкр , то принимается
гипотеза H1.
Пример:
По выборке объема n=7, извлеченной из нормальной двумерной генеральной совокупности, был вычислен коэффициент корреляции Пирсона r=0,57. На уровне значимости α=10% проверить гипотезу H0 о равенстве генерального коэффициента корреляции нулю при конкурирующей гипотезе ρ≠0.
Решение:
Постановка задачи:
H0: ρ=0;
H1: ρ≠0.
Найдем наблюдаемое значение критерия: |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t = |
r • |
n - 2 |
|
→ tнабл |
= |
0.57 • 7 - 2 |
|
≈ 1.55. |
|||||
|
|
|
|
|
|
|
|
|
|||||
1 - r 2 |
|
||||||||||||
|
|
|
|
1 - 0.57 2 |
|
|
|
||||||
Определим значения границ двусторонней критической области из условия, что при малых объемах выборок критерий t распределен (при справедливости нулевой гипотезы) по закону распределения Стьюдента с числом степеней свободы
36
Привлечем таблицу «Критические точки распределения Стьюдента» (она приведена в Приложении); в таблице используем ту ее часть, которая относится к
двусторонней критической области, используем и k=5, на основе этих
значений найдем tкр =2.01.
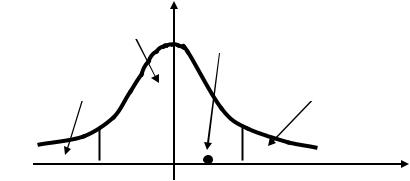
Полученные результаты покажем графически на графике плотности закона распределения Стьюдента, который, как было уже сказано, внешне похож на график плотности стандартного нормального закона распределения:
f(t)
=0.90
tнабл=1.55
/2=0.05 |
/2=0.05 |
tкр= -2.01 0 |
tкр=2.01 |
t |
Поскольку наблюдаемое значение критерия попало в область принятия нулевой гипотезы, то следует принять нулевую гипотезу с уровнем значимости 10%. Это означает, что генеральный коэффициент корреляции равен нулю, т.е. в генеральной совокупности между случайными величинами X и Y линейная связь отсутствует. В этом случае не следует использовать уравнение линейной регрессии для прогнозирования значения одной случайной величины по значению другой случайной величины.
Рассмотрим аналогичный пример, но существенно увеличим в нем объем выборки.
Пример:
По выборке объема n=112, извлеченной из нормальной двумерной генеральной совокупности, был вычислен коэффициент корреляции Пирсона r=0.57. На уровне значимости α=10% проверить гипотезу H0 о равенстве генерального коэффициента корреляции нулю (ρ=0) при конкурирующей гипотезе ρ≠0.
37

Решение:
Постановка задачи:
H0: ρ=0;
H1: ρ≠0.
Найдем наблюдаемое значение критерия:
t = |
r • |
n - 2 |
→ tнабл |
= |
0.57 |
• 112 - 2 |
≈ 7.28. |
||
|
|
|
|
|
|
||||
1- r 2 |
|
||||||||
|
|
|
1- 0.57 2 |
|
|
||||
Определим значения границ двусторонней критической области из условия, что при больших объемах выборок критерий t распределен по стандартному нормальному закону распределения при справедливости нулевой гипотезы (в этом случае пользуемся таблицей интеграла вероятности из Приложения):
=1- =1-0,10=0,90→Ф0(tкр)= /2=0.9/2=0,45→tкр=1.65.
Покажем результаты на графике плотности стандартного нормального закона
распределения:
φ(t)
=0.90
tнабл=7.28
/2=0.05 |
/2=0.05 |
|
tкр= -1.65 0 |
tкр=1.65 |
t |
38
Поскольку наблюдаемое значение критерия попало в критическую область, то следует отклонить нулевую гипотезу в пользу альтернативной гипотезы, т.е. принять,
что коэффициент линейной корреляции в генеральной совокупности значим. Из этого утверждения следует, что между двумя случайными величинами X и Y в генеральной совокупности имеется линейная связь, которая позволяет использовать уравнение линейной регрессии для прогнозирования, т.е., задавая конкретное значение величины
X, получать (прогнозировать) значение другой случайной величины Y хотя бы и с некоторой степенью приближения.
Получился интересный результат, который надо иметь в виду. Он заключается в том, что при больших объемах выборок то же самое значение коэффициента корреляции является значимым, т.е. показывает наличие линейной связи между случайными величинами в генеральной совокупности. В то же время при малых объемах выборок это же значение коэффициента корреляции не является значимым и не позволяет сделать вывод о том, что между случайными величинами в генеральной совокупности имеется линейная связь, поскольку для получения такого вывода в случае малых выборок имеется недостаточное количество экспериментальных данных.
7. Проверка гипотезы о значимости выборочного коэффициента
корреляции Спирмена
Постановка задачи:
H0 : ρSГ = 0;
H1 : ρSГ ≠0.
Здесь через ρSГ обозначен ранговый коэффициент корреляции, связывающий случайные величины в генеральной совокупности (на это указывает индекс «Г»); через
ρS обозначен коэффициент корреляции Спирмена, вычисленный по выборке, иначе выборочный ранговый коэффициент корреляции.
39

Напоминание:
Формулы для вычисления коэффициента Спирмена:
Формула в случае отсутствия |
совпадения ранг ов |
|||
|
n |
2 |
|
|
|
∑ |
|
||
ρs = 1- |
6i=1di |
. |
||
n(n2 |
- 1) |
|||
|
|
|||
Формула |
в случае |
совпадения рангов : |
||||||
|
|
1 |
3 |
n |
2 |
- Ta - Tb |
||
|
|
|
||||||
|
|
6 |
(n - n) - |
∑di |
||||
ρs = |
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ( n3 - n ) - 2T |
|
1 |
(n3 - n) - 2T |
|||||
|
|
6 |
a |
|
6 |
b |
||
|
|
|
|
|||||
Пояснения по формулам можно найти в ссылках [1], [5].
При проверке значимости коэффициента корреляции Спирмена поступают совершенно аналогично тому, как мы поступали, имея дело с коэффициентом Пирсона.
Формулы для вычислений используются те же самые с учетом небольших изменений.
Эти изменения таковы:
Если объем выборки совсем маленький (n<9), то для выяснения значимости коэффициента корреляции нужны специальные таблицы, которые приводятся в специальных руководствах (этот случай мы рассматривать не будем).
Если объем выборки n 9, то при справедливости гипотезы H0 критерий
t = |
ρS • n - 2 |
|||
|
|
|
|
|
|
1 - ρS |
2 |
|
|
|
|
|
||
имеет распределение Стьюдента с k = n - 2 степенями свободы.
40
