Проверка_стат._гипотез,_май_2011

Рассмотрим реализацию приведенного ранее алгоритма проверки статистических гипотез и случая, рассматриваемого в данном разделе, на конкретных примерах.

Пример:

Менеджер отдела сбыта гипермаркета АШАН отслеживает изменение покупательных возможностей посетителей АШАНА. С этой целью он анализирует сумму денег, которую тратит покупатель за одно посещение гипермаркета в течение последнего полугодия. Изучение ситуации полгода тому назад показало, что покупатель АШАНА в среднем за одно посещение гипермаркета осуществляет покупки на сумму 956 руб. В данный момент на основе случайной выборки 76 посетителей АШАНА было найдено, что в среднем покупатель при одном посещении магазина делает покупки на сумму 1021 руб., причем стандартное отклонение для одного покупателя составляет 427 руб. Можно ли на основе этой информации сделать вывод о том, что за полгода среднее количество денег, которые тратит за одно посещение АШАНА покупатель, фактически не изменилось? Принять уровень значимости 5%. (Полагаем, что сумма покупок меняется по нормальному закону распределения).

Решение:

Постановка задачи:

Н0 : m = 956 , здесь m0 = 956 ( или х Г = 956 );

Н1 : m ≠956 ( или х Г ≠ 956).

В данном примере целесообразно говорить в постановке задаче о задании в нулевой гипотезе значения генерального среднего, понимая под этим значением среднюю сумму денег, которую оставляет посетитель АШАНА в магазине при одном его посещении и которая характеризует всю генеральную совокупность покупателей АШАНА.

Введем критерий

t = ( х - m0 ) • n . S

11

В этой формуле х - средняя сумма денег, которую оставляет покупатель за одно посещение АШАНА, вычисленная на основе выборки; S – стандартное отклонение для суммы денег при одном посещении гипермаркета для одного покупателя; n - количество покупателей АШАНА, случайно выбранных для исследования (объем выборки).

Условием задачи заданы следующие экспериментальные значения:

x = 1021; S = 427; n = 76 .

При справедливости нулевой гипотезы поведение этого критерия можно приближенно описать стандартным нормальным законом распределения. Вычислим

наблюдаемое значение критерия на основе экспериментальных значений:

Далее следует определить границы двусторонней критической области на основе табличного решения следующего уравнения. Здесь пользуемся тем, что выборка велика

(n больше 30), тогда

Отсюда на основе таблицы интеграла вероятностей Ф0, приведенной в Приложении, по значению функции Ф0 находим значении аргумента: tкр=1.96.

Изобразим имеющие результаты графически, используя график плотности стандартного нормального закона распределения:

=0.95 φ(t)

12

Поскольку наблюдаемое значение критерия попало в область естественных значений критерия, т.е. тех значений критерия, при которых нулевая гипотеза принимается как не противоречащая экспериментальным данным, то в результате решения задачи следует сделать такой вывод: принимаем с уровнем доверия в 95% утверждение о том, что средняя сумма денег, которую оставляет в АШАНЕ покупатель за одно посещение гипермаркета, значимо не изменилась за полгода. Таким образом, следует принять как верное то утверждение, которое было сформулировано в нулевой гипотезе (говорят:

принимаем нулевую гипотезу).

Покажем, как изменилось бы решение задачи, если бы мы альтернативную гипотезу поставили другую.

Иная постановка задачи:

(более того, отметим, что именно такая постановка задачи представляется более естественной в данном случае, поскольку экспериментальные данные показали повышение величины средней суммы денег, оставляемой в магазине покупателем):

Н0 : m = 956 , здесь m0 = 956 ( или хг = 956 );

Н1 : m > 956 ( или хг > 956).

Изменение в решении задачи касаются только вида критической области. В этом случае следует использовать правостороннюю критическую область, при этом значение границы критической области изменится.

Теперь границу критической области следует искать на основе табличного решения другого уравнения

Ф0 (tкр ) = γ - 0.5; Ф0 (tкр ) = 0.95 - 0.5 = 0.45.

По таблице интеграла вероятностей Ф0 находим tкр ≈ 1.65. Снова покажем полученные результаты на графике плотности стандартного нормального закона распределения:

13

φ(t)

=0.95

tнабл=1.33

=0,05

Поскольку по-прежнему наблюдаемое значение критерия попало в область принятия нулевой гипотезы, то ранее полученный вывод не изменился, т.е. мы принимаем нулевую гипотезу об отсутствии значимых изменений в той сумме денег,

которую в среднем тратит покупатель за одно посещение АШАНА.

Замечание: Следует отметить, что в тех случаях, когда наблюдаемое значение параметра оказывается вблизи границы критической области, вывод в результате решения задачи может быть изменен на противоположный в том случае, когда от двусторонней критической области переходим к односторонней критической области,

или же в том случае, когда задаем другой уровень значимости (другой уровень доверия).

Решим аналогичную задачу в ситуации, когда для получения выводов используется выборка малого объема (объем выборки не превосходит 30).

Сохраним те же исходные данные, что и в предшествующих двух вариантах за исключением величины объема выборки. Итак, пусть по случайной выборке было найдено, что в среднем покупатель при одном посещении магазина тратит 1021 руб. со стандартным отклонением 427 руб. Сохраним также уровень значимости. Пусть теперь объем выборки равен 15 покупателям.

Постановка задачи:

Н0 : m = 956 , здесь m0 = 956; Н1 : m > 956.

14

Критерий t определяется той же самой формулой, но в случае выборок малого объема при справедливости нулевой гипотезы критерий t подчиняется распределению Стьюдента с числом степеней свободы k = n - 1. Поэтому при определении границ критической области следует пользоваться таблицей критических точек распределения Стьюдента для односторонней (при данной альтернативной гипотезе) критической области. Эту границу мы найдем на основе числа степеней свободы и на основе заданного уровня значимости = 0.05 (в данном случае нужно выбирать уровень значимости в нижней строке таблицы). Соответствующая таблица находится в Приложении. Находим по k=14 и =0,05 значение tкр =1.76.

Вычислим наблюдаемое значение критерия

Отметим, что внешне график плотности закона распределения Стьюдента похож на график плотности стандартного нормального закона распределения, только линия плотности для него идет более полого по сравнению с графиком плотности стандартного нормального закона распределения (меньше подъем графика в центральной его части и дальше отстоят периферийные части графика от горизонтальной оси). Чтобы подчеркнуть, что в данном случае речь идет об ином графике по отношении к графику плотности стандартного нормального закона распределения, вертикальную ось графика обозначим f(t) вместо ᵩ (t):

f(t)

=0.95

tнабл=0.59

=0.05

На основе сравнения положений критического и наблюдаемого значений критерия делаем вывод о том, что следует принять нулевую гипотезу с уровнем доверия в 95% как не противоречащую экспериментальным данным, т.е. в данном случае вывод по задаче не изменился.

Замечание:

Тот же самый первый вариант задачи можно было бы решить иначе, с

привлечением понятия доверительного интервала. Смысл такого подхода к решению

задачи основан на следующем утверждении:

Если заданное в условии задачи значение параметра m0 попадает в доверительный интервал, соответствующий заданному уровню значимости, то утверждение нулевой гипотезы принимается с тем же уровнем значимости. Если же

заданное значение m0 оказывается вне доверительного интервала, то следует отвергнуть нулевую гипотезу в пользу альтернативной гипотезы. Обоснование данного подхода к решению задачи заключено в том факте, что при построении доверительного интервала и при выстраивании критической области выполняются аналогичные преобразования, которые приводят к одинаковым формулам.

Напомним формулу, по которой находится двусторонний доверительный интервал для математического ожидания (генерального среднего) нормально

распределенной генеральной совокупности:

Решим вариант данной задачи в первоначальной постановке на основе

применения доверительного интервала.

Постановка задачи:

Н0 : m = 956 ,здесь m0 = 956 ( или х Г = 956 );

Н1 : m ≠956 ( или х Г ≠ 956).

16

Будем использовать прежние экспериментальные значения в вычислениях:

x = 1021; S = 427; n = 76.

Используем прежний уровень значимости =5%, для которого было найдено критическое значение параметра tкр=1.96.

Вычислим доверительный интервал на основе исходных значений:

Поскольку значение m0 = 956 попадает в найденный доверительный интервал, то утверждение, составляющее содержание нулевой гипотезы, следует принять с уровнем доверия в 95%. Естественно, что получен тот же вывод, который получили при первоначальном способе решения этой задачи.

Из данного способа решения также совершенно очевидным является и другой

вывод:

Утверждение, составляющее содержание нулевой гипотезы, не является единственно верным. Можно было бы изменить содержание нулевой гипотезы и вместо ранее заданного значения m0 = 956 в нулевой гипотезе задать, например, значение m0 =1100. Это значение также попадает в доверительный интервал и, следовательно,

не противоречит экспериментальным данным, поэтому и значение m0 =1100 также могло служить содержанием утверждения нулевой гипотезы. Мы должны были бы принять новое значение m0 =1100 как не противоречащее экспериментальным данным, причем это значение мы также приняли бы с тем же уровнем доверия.

17

3. Проверка гипотезы о числовом назначении вероятности

биноминального закона распределения (о числовом значении

генеральной доли)

Рассмотрим генеральную долю признака WГ =K/N – это часть объектов генеральной совокупности, обладающих определенным признаком (N – объем генеральной совокупности; K – количество объектов генеральной совокупности,

обладающих данным признаком). Эту величину можно также трактовать как вероятность р того, что случайно выбранный объект из генеральной совокупности будет обладать этим признаком, причем полагаем, что величина вероятности не меняется при переходе от одного объекта к другому объекту и имеет место независимость появления признака для каждого объекта генеральной совокупности, т.е.

рассматривается модель явления, присущая биномиальному закону распределения

признака.

Вывод: постановку задачи можно осуществлять как в терминах «генеральная доля признака», так и в терминах «вероятность биномиального закона распределения».

Все зависит от того, как поставлена исходная задача, какой акцент мы хотим придать

получающимся результатам.

Выборочной долей признака является величина w = k/n – это точечная оценка генеральной доли и, одновременно, точечная оценка вероятности в биномиальном законе распределения (n – объем случайной выборки; k – количество объектов в

выборке, обладающих данным признаком).

Здесь р0 – заданная условием задачи константа.

18

Для задач этого типа вводится критерий

который и будем использовать для проверки нулевой гипотезы. Показано, что в случае справедливости нулевой гипотезы этот критерий имеет закон распределения,

приближающийся к стандартному нормальному закону распределения.

При альтернативной гипотезе типа (1) строим двустороннюю критическую область, при альтернативных гипотезах типа (2) строим одностороннюю критическую область (левую или правую).

Процедура проверки справедливости нулевой гипотезы полностью повторяет тот алгоритм, который был реализован в предыдущем разделе.

Рассмотрим решение конкретного примера.

Пример:

Известно, что примерно 83% студентов факультета менеджмента защищают диплом на отличную оценку. На основе наблюдений этого года было выяснено, что из

100 случайно отобранных дипломников отличную оценку получил 91 студент. Можно ли с 98% уровнем доверия сказать, что наблюдения этого года не противоречат ранее сделанному статистическому выводу?

Решение:

Постановка задачи:

H0: WГ = 0,83; здесь р0=0.83;

H1: WГ > 0,83.

выбранный студент этого факультета получит отличную оценку за диплом):

19

правосторонней критической области, с помощью интеграла вероятностей, применяя соответствующую таблицу, приведенную в Приложении, и используя обычные формулы для вычисления вероятности попадания стандартной нормально распределенной случайной величины в заданный интервал:

P (tкр п < t < + 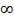) = 0,02 → P (tкр п < t < + 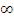) = Ф0 (+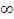) - Ф0 (tкр п) = = 0.5 - Ф0 (tкр п) = 0,02→Ф0 (tкр п) = 0,48 → tкр п ≈2.04.

Покажем полученные результаты на графике плотности стандартного нормального закона распределения:

φ(t)

γ=0.98

α=0.02

0 tкр п ≈2.04 tнабл.≈2.13

20