Проверка_стат._гипотез,_май_2011

Поскольку наблюдаемое значение критерия попадает в область критических значений этой случайной величины, то следует отвергнуть нулевую гипотезу как противоречащую экспериментальным данным и, следовательно, принять альтернативную гипотезу. Таким образом, утверждение, высказанное в нулевой гипотезе, противоречит экспериментальным данным и поэтому не может быть признано верным. В действительности доля студентов, получивших отличную оценку за диплом, значимо превосходит ту долю, которая указана в нулевой гипотезе. Однако в данной ситуации вывод по задаче следует сделать иной, если задать другое значение уровня значимости.

Давайте решим эту же самую задачу, сделав в ней единственное изменение:

примем = 0,01 (ранее было задано значение α = 0,02).

Решение:

Постановка задачи:

H0: WГ = 0,83, здесь р0=0,83;

H1: WГ > 0,83.

Экспериментальные данные: n = 100, k = 91.

Наблюдаемое значение tнабл в этом случае не изменяется; изменяется лишь tкр п .

Найдем новое значение tкр п:

P (tкр п < t < + 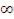) = 0,01→P (tкр п < t < + 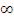)= Ф0 (+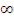) - Ф0 (tкр п)=

=0,5 - Ф0 (tкр п)=0,01→Ф0 (tкр п) = 0,49→ tкр п ≈2.32.

Покажем числовые результаты на графике плотности стандартного нормального

закона распределения:

21

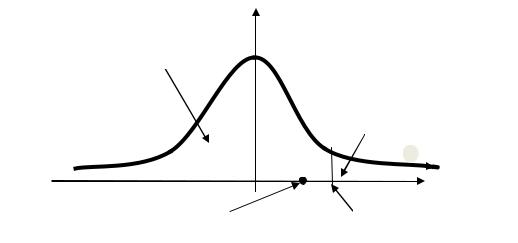
φ(t)

γ=0.99

α=0.01

tнабл.≈2.13 tкр п ≈2.32

В этом случае из-за изменения положения границы критической области наблюдаемое значение критерия попало в область принятия нулевой гипотезы,

следовательно, вывод в результате решения примера мы должны сделать иной.

Принимаем нулевую гипотезу о том, что генеральная доля студентов, которые сдают диплом на отлично, можно считать равной 83%, поскольку значения выборочной доли отличников и заявленного значения генеральной доли отличников различаются незначимо, несущественно. Решение этой задачи позволяет отметить одну особенность,

о которой уже говорилось: когда наблюдаемое значение критерия находится недалеко от границы критической области, то при изменении уровня значимости вывод по задаче можно получить противоположный по своему смыслу (и этим данная ситуация неприятна). Поэтому при решении задачи надо обязательно указывать, при каком уровне значимости был получен данный вывод и, возможно, отметить, что вывод может быть иным при изменении принятого в задаче уровня значимости.

Решим еще один пример на проверку такой же гипотезы.

Пример (предложен Аленой Бут, студенткой факультета менеджмента ВШЭ):

На основании предшествующих исследований известно, что доля крупных западноевропейских бизнесменов, имеющих счета в швейцарских банках, составляет примерно 78%. Исследовательский центр Германии «Meinungsumfrage» сделал

22

случайную выборку, отобрав 670 крупных бизнесменов Западной Европы, и установил,

что 510 из них хранят свои сбережения на счетах в швейцарских банках.

На основе применения доверительного интервала проверить справедливость утверждения, что и в настоящее время доля крупных бизнесменов, имеющих счета в швейцарских банках, также составляет 78%.

Решить эту же задачу, применяя традиционную постановку задачи с введением основной и альтернативной гипотез.

В обоих случаях принять уровень доверия равным 1%.

Решение:

Экспериментальные данные: n = 670, k = 510; кроме того, α = 0,01.

Поскольку выборка большая, то доверительный интервал находится по формуле

Вычислим величину предельной ошибки выборки:

Вычислим доверительный интервал:

I0.99 = (0.76 - 0.04;0.76 + 0.04) = (0.72;0.80).

23

Данный доверительный интервал с вероятностью 99% накрывает генеральную долю западноевропейских бизнесменов, хранящих свои сбережения в швейцарских банках.

Поскольку значение генеральной доли 0.78, заданное условием задачи, попадает в этот доверительный интервал, то, следовательно, с уровнем доверия в 99% (или с уровнем значимости в 1%) можно принять нулевую гипотезу как не противоречащую опытным данным.

Решим этот же пример на основе алгоритма проверки статистических гипотез.

Постановка задачи:

H0: WГ = 0.78, здесь р0 = 0.78;

H1: WГ < 0.78.

Экспериментальные данные: n = 670, k =510; кроме того, α = 0,01.

Значение выборочной доли уже было найдено ранее:

Вычислим значение критерия, который при справедливости основной гипотезы имеет приближенно стандартное нормальное распределение:

Найдем границу левосторонней критической области на основе табличного решения уравнения, которое позволяет вычислить вероятность попадания стандартной нормально распределенной случайной величины в заданный интервал. Для решения используем таблицу значений функции Ф0, приведенной в приложении:

24

P (tкр л < t < + ) = 0.99→P (tкр л < t < + )= Ф0 (+) - Ф0 (tкр л)=

=0.5 - Ф0 (tкр л)=0.99→Ф0 (tкр л) = - 0.49→Ф0 (-tкр л) = 0.49→ tкр л ≈-2.32.

Покажем результаты на графике плотности стандартного нормального закона распределения:

φ(t)

γ=0.99

α=0.01

На основе данного графика, сравнивая взаимное расположение наблюдаемого значения критерия и границы левосторонней критической области, следует сделать вывод о принятии нулевой гипотезы как не противоречащей экспериментальным данным с уровнем доверия в 1%.

Замечание: получены одинаковые выводы независимо от способа решения на основе использования доверительного интервала и на основе алгоритма проверки статистической гипотезы.

Пример (предложен студенткой факультета менеджмента Клишиной Ириной):

Главный врач ветеринарной клиники утверждает, что не менее 70 % его пациентов после приёма новейших лекарств верно служат своим хозяевам не болея на протяжении трех лет. Можно ли считать это утверждение верным, если из 100

пациентов ветеринарной клиники 59 остаются здоровыми после приема таблеток ещё три года? Принять уровень значимости 5%.

25

Решение:

Постановка задачи:

H0: p = 0.70 (р0 = 0.70;)

H1: p < 0.70 (альтернативная гипотеза поставлена на основе результатов выборки).

Экспериментальные значения: n=100; k=59.

Найдем границу левосторонней критической области. Так как n>30, то находим tкр л с помощью интеграла вероятностей; его значения взяты из таблицы, находящейся в Приложении:

P (tкр л < t < + ) = 0.95 →P (tкр л < t < + )=: Ф0 (+) - Ф0 (tкр л) = =0.5 + Ф0(-tкр л) = 0.95 → Ф0 (-tкр л) = 0.45 → tкр л = -1.65.

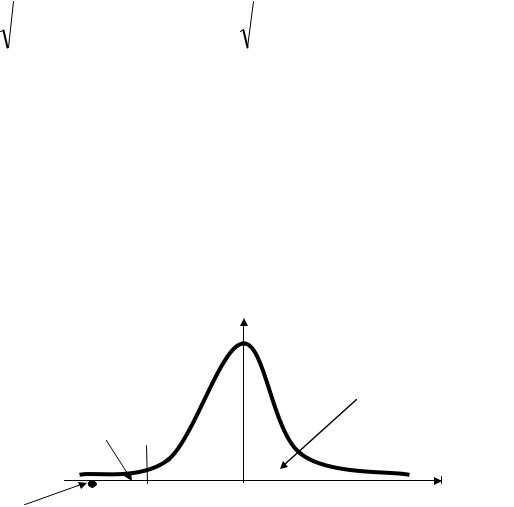
Покажем получившиеся результаты на графике плотности стандартного

нормального закона распределения:

φ(t)

γ=0.95

α=0.05

t

26

Поскольку наблюдаемое значение критерия попало в область критических значений критерия, то отвергаем нулевую гипотезу как противоречащую экспериментальным данным и принимаем, следовательно, альтернативную гипотезу H1,

т.е. можно сказать, что менее 70% пациентов после приёма лекарств верно прослужат своим хозяевам ещё три года (утверждение врача клиники чрезмерно оптимистично).

4. Проверка гипотезы о равенстве математических ожиданий

(о равенстве генеральных средних) двух нормально распределенных

генеральных совокупностей

Пусть имеются две нормально распределенные генеральные совокупности,

причем в первой совокупности изучаемый признак X~N(m1; 1), во второй совокупности изучаемый признак Y~N(m2; 2), т.е. каждый признак имеет нормальный закон распределения со своими параметрами.

Мы в дальнейшем будем рассматривать ситуации, относящиеся к случаям больших выборок из этих двух генеральных совокупностей: n1>30, n2>30. Случаи малых выборок анализируются в соответствующих разделах учебников; здесь такие ситуации не рассматриваются.

Постановка задачи:

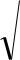
достаточно хорошо аппроксимируются выборочными дисперсиями, т.е. можно считать,

что

Эта случайная величина при справедливости нулевой гипотезы приближенно имеет стандартный нормальный закон распределения.

Решим конкретную задачу, в которой реализуется описанный выше подход.

Пример:

Проводится сравнение роста 20-летних юношей, проживающих в Москве и в Новосибирске. На основе двух случайных выборок, выполненных в двух городах, были получены следующие данные. В Москве отобрали 75 юношей. Был измерен рост каждого юноши. На основе измерений были вычислены две характеристики: средний рост юношей, который оказался равным 179 см, и стандартное отклонение, которое оказалось равным 8 см. В Новосибирске были случайно отобраны 57 юношей, их средний рост оказался равным 176 см со стандартным отклонением 10 см. На основе этих экспериментальных данных следует проверить гипотезу о равенстве средних величин роста московских и новосибирских 20-летних юношей (о равенстве генеральных средних). Принять доверительную вероятность равной 90%.

Предполагается, что рост юношей подчиняется нормальному закону распределения.

28

Иная постановка вопроса к тем же исходным данным может звучать так:

Следует выяснить, значимо или же незначимо отличаются друг от друга выборочные средние значения ростов юношей. Если будет показано, что выборочные средние отличаются незначимо, то отсюда можно будет сделать вывод о справедливости нулевой гипотезы, т.е. вывод о примерном равенстве генеральных средних значений роста юношей, проживающих в различных городах. В противном случае будет сделан вывод о существенном различии генеральных средних значений роста юношей, проживающих в этих городах.

Решение:

Постановка задачи:

H 0 : xГ = yГ ,

H 1 : xГ ≠yГ

Здесь xГ - средний рост двадцатилетних юношей Москвы; yГ - средний рост двадцатилетних юношей Новосибирска.

При такой постановке задачи следует строить двустороннюю критическую область. Определим границы этой области на основе табличного решения уравнения:

Вычислим на основе экспериментальной информации наблюдаемое значение критерия, который при справедливости нулевой гипотезы приближенно имеет стандартный нормальный закон распределения:

29

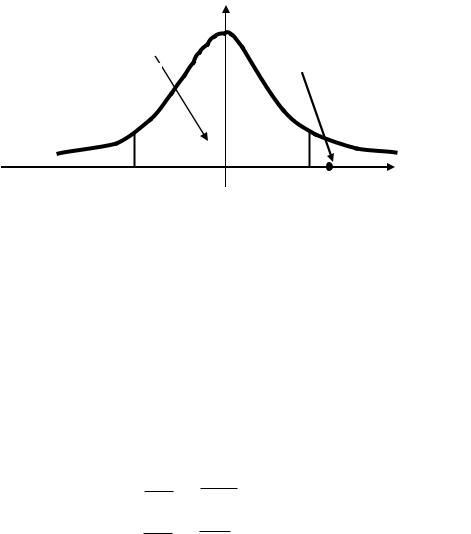
Изобразим результаты графически на графике плотности стандартного

нормального закона распределения:

Поскольку наблюдаемое значение критерия попало в критическую область значений параметра, то следует отвергнуть основную гипотезу в пользу альтернативной гипотезы и сказать, что средний рост московских и новосибирских 20-летних юношей отличается значимо.

Решим эту же задачу с теми же самыми исходными данными в случае иной,

более естественной в данном случае альтернативной гипотезой. Ее естественность обусловлена конкретными экспериментальными значениями.

Постановка задачи:

H0 : xГ = yГ ,

H1 : xГ > yГ

Такая постановка задачи требует построения правосторонней критической области. Найдем границу правосторонней критической области:

Ф0 (tкр п )= 0.5 - α → Ф0 (tкр п )= 0.50 - 0.10 = 0.40 → tкр п ≈ 1.28.

В данном случае наблюдаемое значение критерия не меняется.

Покажем результаты на графике плотности стандартного нормального закона распределения:

30