Проверка_стат._гипотез,_май_2011

Значение tкр находим по таблице критических точек распределения Стьюдента по значениям и k для двусторонней критической области (таблица приведена в Приложении). Вычисляем наблюдаемое значение критерия tнабл на основе приведенной

выше формулы. Если то принимается гипотеза H0, если то

принимается гипотеза H1, т.е. в этом случае считаем доказанным утверждение, что коэффициент корреляции является значимым и в генеральной совокупности между порядковыми признаками имеется корреляционная связь.

Если объем выборки n >30, то вместо закона Стьюдента используем стандартный нормальный закон распределения для определения tкр.

Рассмотрим пример на определение значимости рангового коэффициента.

Пример:

Для 15 пар порядковых переменных (x, y) был вычислен коэффициент

Решение:

Постановка задачи:

H0 : ρS Г = 0;

H1 : ρS Г ≠0.

Найдем наблюдаемое значение критерия:

Найдем значения границ двусторонней критической области из условия, что при

малых объемах выборок критерий t распределен (при справедливости нулевой

41

гипотезы) по закону распределения Стьюдента с числом степеней свободы

k=15-2=13.

На основе таблицы «Критические точки распределения Стьюдента» (см.

Приложение) найдем границы двусторонней критической области на основе и

k=13. Значение границы оказывается равным

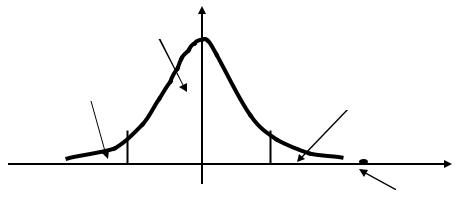
Полученные результаты покажем графически, используя график плотности закона распределения Стьюдента:

f(t)

=0.95

Поскольку наблюдаемое значение критерия попало в критическую область, то следует отклонить нулевую гипотезу в пользу альтернативной гипотезы. Это означает,

что коэффициент ранговой корреляции значим. Иными словами можно сказать, что между двумя порядковыми случайными величинами X и Y в генеральной совокупности имеется значимая связь.

Замечание:

Если бы в данном примере объем выборки был бы более 30, то находили бы границы двусторонней критической области на основе уравнения: Ф0(tкр) = /2.

В остальном вычисления выполнялись бы по тем же формулам.

42

8. Критерий знаков

Критерий знаков не связан с заданием каких-то конкретных значений параметров распределения, и поэтому на основе этого критерия формулируются так называемые непараметрические статистические гипотезы.

Это самый простой критерий непараметрической статистики. Простота критерия объясняется двумя причинами:

1)Не делается предположение о том, что генеральная совокупность имеет нормальное распределение или какое-то другое распределение. Единственное предположение – распределение должно быть непрерывным.

2)Критерий знаков использует только знаки различий между двумя числами, а не их количественную меру. Поэтому иногда его называют «ранговый критерий проверки гипотез».

Пусть имеются две выборки одинакового объема n, и эти выборки ранжированы, т.е

значения в выборках расположены по мере возрастания:

x1<x2<…<xn и y1<y2<…<yn.

Введем разность ri= xi - yi. Будем исследовать величину разности ri. Если мы найдем, что большинство пар значений (xi;yi) мало отличаются друг от друга, т.е.

значения ri окажутся достаточно малыми, то это позволит нам считать, что все xi и yi

меняются примерно одинаковым образом, т.е. выборки извлечены из одной и той же генеральной совокупности (и в этом состоит суть утверждения, составляющего содержание нулевой гипотезы). В противном случае следует считать выборки извлеченными из разных генеральных совокупностей.

Конкретные формы задания нулевой и альтернативной гипотез могут быть различными в зависимости от конкретной ситуации, рассматриваемой в задаче. Здесь будет рассмотрено только два варианта задания нулевой гипотезы; об их содержании будет сказано далее.

43

Исследуем знаки разностей ri и найдем число положительных разностей

(положительное значение разности назовем успехом), т.е. найдем число успехов,

которое обозначим величиной k.

В случае справедливости нулевой гипотезы положительные и отрицательные разности ri будут появляться с одинаковой вероятностью. Следовательно, задание гипотезы H0 возможно в двух форматах, которые будут рассмотрены в этом разделе.

Первый вариант задания нулевой гипотезы:

р= Р(x-y>0)=Р(x-y<0)=q=1-p= 0.5;

Более компактный вариант задания нулевой гипотезы: p= 0.5.

Второй вариант задания нулевой гипотезы:

xГ yГ

Во втором случае предполагается проверить, равны ли друг другу генеральные средние для двух генеральных совокупностей. Понятно, что приведенные варианты формулировок нулевой гипотезы связаны между собой. В самом деле, если генеральные средние равны, то число положительных разностей ri должно быть примерно равно числу отрицательных разностей.

Для первого варианта задания нулевой гипотезы постановка задачи выглядит следующим образом:

H0: p= 0.5;

H1: p ≠ 0.5.

Для второго варианта задания нулевой гипотезы постановка задачи такова:

44

Алгоритм реализации критерия знаков таков:

1.Рассматривают серию из n испытаний; ранжируют две выборки xi, yi,

(i=1,2,…,n); анализируют разности ri=xi - yi; подсчитывают число положительных разностей. Если разность ri окажется равной нулю, то ее исключают из рассмотрения.

Выясняют число положительных разностей - это число успехов k.

Замечание: можно было бы совершенно аналогично рассматривать и отрицательные разности.

2.Для получения выводов используется критерий следующего вида:

который получен на основе биномиального закона распределения с вероятностью,

равной 0.5 (именно это значение вероятности заложено в нулевой гипотезе).

При справедливости гипотезы H0 наблюдаемое значение критерия Wнабл(n;k)

принимает естественные для этой случайной величины значения (не слишком большие и не слишком маленькие).

Отметим, что W(n; 0)≈0 , а W(n; n)=1.

На основе свойств биномиальных коэффициентов для облегчения вычислений целесообразно использовать равенство, уменьшающее количество вычислений:

W(n; k) = =1 – W(n; n-k-1).

Это равенство удобно использовать, когда k>n/2.

Замечание: Критерий W(n;k) – это вероятность такого события: «Число успехов наблюдалось от 0 до k раз», что соответствует такому утверждению: критерий W(n;k)-

это функция распределения случайной величины, подчиняющейся биномиальному закону распределения, в котором значение вероятности равно 0.5.

3.Критические области определяются видом альтернативной гипотезы H1.

Рассмотрим три возможных вида альтернативной гипотезы:

a) H1: xГ ≠yГ .

45

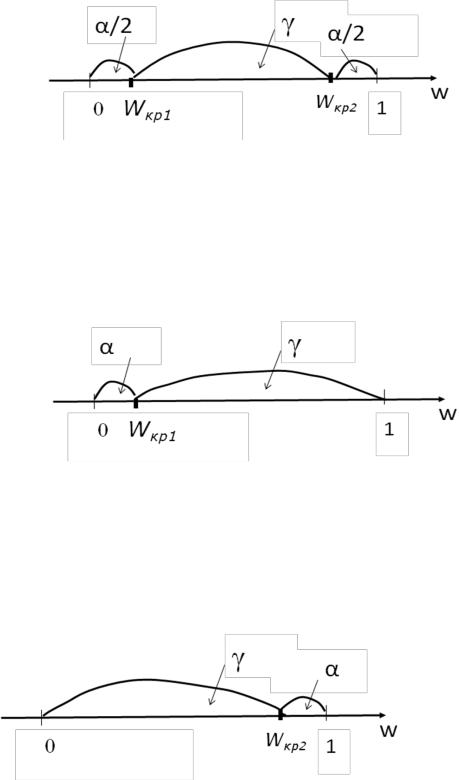
В этом случае выстраивается двусторонняя критическая область. В критическую область наблюдаемое значение критерия попадает тогда, когда положительных разностей либо слишком много, либо слишком мало. Покажем возникающую в этом случае ситуацию графически:

б) H1: xГ < yГ .

В этом случае выстраивается левосторонняя критическая область. В

критическую область значение критерия попадает тогда, когда положительных разностей мало (мало успехов):

46

4.Вычисление критерия W(n;k) проводят при малых выборках (n≤30). При

больших выборках (n>30) биномиальный закон распределения удобно заменить стандартным нормальным законом распределения (вычисления на основе критерия

W(n;k) становятся очень громоздкими, в то время как применение стандартного нормального закона распределения существенно упрощает вычисления), поэтому при n>30 обычно вводят иной критерий, поскольку вычисления по нему существенно упрощаются.

Этот критерий, который при справедливости гипотезы H0 может быть приближенно описан стандартным нормальным законом распределения, определяется

n

Рассмотрим пример на применение критерия знаков.

Пример:

Один хиромант утверждает, что он по линиям руки человека может безошибочно указать год его рождения, не имея об этом человеке никакой предварительной информации. С хиромантом было поставлено 11 экспериментов, и

результаты оказались следующими: + + - - + - + - + + + , где знак «+» ставился тогда, когда хиромант давал правильный ответ, и знак «-», когда хиромант ошибался

(n=11, k=7). Проверить при помощи критерия знаков с уровнем значимости = 0.05

справедливость утверждения хироманта.

Решение:

47

Постановка задачи:

Н0: p = 0.5 (вероятность правильного ответа равна 0.5, т.е. хиромант

в половине случаев дает правильный ответ, а в половине случаев ошибается; это означает, что он не обладает способностью давать правильный ответ, используя руку клиента);

Н1: p > 0.5 (вероятность правильного ответа более 0.5, т.е. хиромант

чаще дает правильный ответ, а ошибается реже; это означает, что он обладает способностью считывать информацию с руки клиента и поэтому давать правильный ответ).

В качестве критерия используем случайную величину вида:

W (n, k) 21n k Cni ,

i 0

W(n; k) = =1 – W(n; n-k-1).

Вычислим наблюдаемое значение критерия (воспользуется тем, что 7>11/2),

Покажем полученный результат графически, используя горизонтальную ось, на которой покажем границу правосторонней критической области и наблюдаемое значение критерия:

48

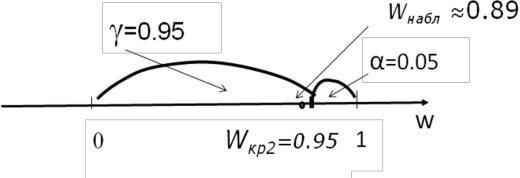
Поскольку наблюдаемое значение критерия попало в область естественных значений критерия, то нам следует принять справедливость нулевой гипотезы,

поскольку высказанное в ней утверждение не противоречит экспериментальным данным (с уровнем доверия к этому высказыванию в 95%). Таким образом, несмотря на то, что хиромант дал достаточно много правильных ответов, но их оказалось недостаточно для того, чтобы признать справедливость его утверждения. Для того,

чтобы утверждение хироманта можно было считать справедливым, требуется большее количество правильных ответов. Итак, на основе экспериментальных данных признаем высказывание хироманта необоснованным.

Решим аналогичную задачу в ситуации, когда n становится большой величиной.

Пример:

Один хиромант утверждает, что он по линиям руки человека может безошибочно указать год его рождения. С хиромантом было проведено 110

экспериментов, при этом им было дано 70 правильных ответов, остальные ответы оказались неверными. Проверить при помощи критерия знаков с уровнем значимости

= 0.05 справедливость утверждения хироманта.

Решение:

Постановка задачи:

Н0: p = 0.5 (в дальнейшем используется р0 =0.5);

Н1: p > 0.5.

49

Экспериментальные значения были получены такие: n=110, k=70.

Вычислим на основе экспериментальных данных выборочную долю:

Вычислим наблюдаемое значение критерия критерий t , который при больших объемах выборки ведет себя примерно как стандартная нормально распределенная случайная величина:

вероятностей (см. таблицу в Приложении):

P (tкр п < t < +∞) = 0,05 →P (tкр п < t < +∞) = Ф0 (+∞) - Ф0 (tкр п) = =0,5 - Ф0(tкр п) = 0,95 → Ф0 (tкр п) = 0.45 → tкр п =1.65.

Покажем полученные результаты на графике плотности стандартного

нормального закона распределения:

φ(t)

γ=0.95

α=0.05

0 tкр п ≈1.65 tнабл.≈2.83

50