2.1.2. Численное решение линейных дифференциальных уравнений методом разложения в ряд Тейлора

Рассмотрим матричное однородное линейное дифференциальное уравнение

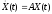(2.1.1)

Одним из методов численного решения дифференциальных уравнений является разложение решения на шаге h в ряд Тейлора [2.4] относительно предыдущего момента времени t

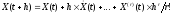(2.1.2)

Значения входящих в ряд Тейлора производных определим из уравнения (1):

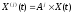, j = 1…r

Подставив эти значения в (2), получим:

X(t+h) = [I+Ah+A²h²/2…(Ah)^r/r! …]X(t) (2.1.3)

Матричный ряд в квадратной скобке представляет собой матричную экспоненту:

e^Ah = [I+Ah+A²h²/2(Ah)^r/r! …]

(2.1.4)

Таким образом, точное решение уравнения (1) на шаге можно представить в виде:

X(t+h) = e^AhX(t) (2.1.5)

При численном решении ряды в соотношениях (2), (3) и (4) усекаются. Порядком r метода численного решения называется максимальная степень шага h , оставляемая в разложении. Представим матричный экспоненциальный ряд в виде суммы:

e^Ah = e^Ah + de^Ah , e^Ah = I+Ah+A²h²…(Ah)^r/r! ,

(2.1.6)

de^Ah = (Ah)^r+1/(r+1)! +…

где e^Ah - усеченная экспонента, de^Ah - отбрасываемая часть экспоненциального ряда (4).

Результат X(t+h) приближенного численного решения уравнения (1) на шаге h методом r -го порядка можно представить в следующем виде:

X(t+h) = [I+Ah+A²h²…(Ah)^r/r!]X(t) = e^AhX(t) (2.1.7)

Умножая матрицы (6) справа на X(t) с учетом (7), получим

X(t+h) = e^AhX(t) = e^AhX(t) + de^AhX(t) = X(t+h) + dX(t+h) ,

(2.1.8)

где ошибка численного решения на шаге h или локальная ошибка метода

r -того порядка равна:

dX(t+h) = de^AhX(t) = [(Ah)^r+1/(r+1)! +…]X(t) (2.1.9)

Для приближенной оценки локальной ошибки можно использовать соотношение

dX(t+h)[ (Ah)^r+1/(r+1)! ]X(t)

2.1.3. Выражение ошибки численного решения через изменения коэффициентов дифференциального уравнения

Сравнивая точное решение (5) с приближенным численным решением (7) можно видеть, что процедура вычисления на шаге h для них одинакова: предыдущее значение X(t) умножается слева на некоторую матрицу. Однако в точном решении X(t) умножается на матрицу полной экспоненты e^Ah , а в приближенном - на матрицу усеченной экспоненты е^Ah.

Зададимся вопросом: для какого, измененного по отношению к (1), уравнения приближенное численное решение X(t+h) из(7) является точным?

Измененное уравнение (1) запишем следующим образом:

(2.1.10)

Его точное решение на шаге h

X(t+h) = e^(A+dA)hX(t) (2.1.11)

Приравняв выражения (2) и (11), можно получить :

e^(A+dA)h = e^Ah (2.1.12)

Это уравнение определяет матрицу dA из уравнения (10).

Матричную экспоненту (12) представим в виде:

e^(A+dA)h = e^Ahe^dAh

Отсюда и из (6) можно получить:

e^dAh – I = - e^-Ah de^Ah (2.1.13)

Представив матрицы в виде степенных разложений и оставляя только главные члены, получим приближенное соотношение :

dAh- (Ah)^r+1 /(r+1)! (2.1.14)

Соотношения (13) и (14) позволяют вычислить матрицу dA, входящую в измененное уравнение (10). Точное решение этого уравнения совпадает с приближенным численным решением уравнения (1) методом r-того порядка. Таким образом, матрицу dA можно использовать в качестве характеристики погрешностей численного решения через изменение коэффициентов дифференциального уравнения (1).

Используя (14) можно выразить локальную ошибку численного решения (9) через dA:

dX(t+h) = - dAhX(t)

Если по условиям решаемой задачи можно сформулировать допустимые изменения коэффициентов dA, то соотношения (13) и (14) позволят осуществить предварительный выбор порядка метода r и шага дискретизации h.