
- •Раздел 1. Фильтрация помех при моделировании
- •Раздел 1. Фильтрация помех при моделировании
- •1.1 Алгоритм разложения сигнала по неортогональному базису
- •1.2. О сходимости разложений
- •1.3. Разложение дискретных функций
- •Экспериментальные данные обычно являются дискретными
- •Функциями времени, то есть представляют собой набор
- •Отсчетов:
- •1.4. Фильтрующие свойства разложений
- •1.5. Оценка уровня помех в обрабатываемой реализации
- •1.6. Оценка погрешностей разложения
- •1.8 Оценка погрешностей разложения методом статистического моделирования
- •Раздел 2. Моделирование непрерывных систем
- •2.1. Цифровое моделирование непрерывных динамических систем
- •2.1.1 Методы цифрового моделирования
- •2.1.2. Численное решение линейных дифференциальных уравнений методом разложения в ряд Тейлора
- •2.1.3. Выражение ошибки численного решения через изменения коэффициентов дифференциального уравнения
- •2.1.4. Выражение ошибки численного решения через изменение корней характеристического уравнения
- •2.1.5. Устойчивость численного решения
- •2.1.6. Повышение точности численного решения методом коррекции уравнений движения
- •2.2. Погрешности аналогового моделирования
- •2.2.1. Особенности аналоговой вычислительной техники
- •2.2.2. Взаимосвязь приращений корней и коэффициентов характеристического уравнения
- •2.2.3. Влияние аналогового интегратора на корни характеристического уравнения
- •2.3. Погрешности полунатурного моделирования
- •Упражнения
- •Литература
1.2. О сходимости разложений
При заданном базисе фi(t) коэффициенты Ui,k системы уравнений (9) могут быть вычислены заранее. В этом случае определение коэффициентов разложения Ci сводится к вычислению правых частей Vi по (16) и решению системы линейных уравнений (9) или, что эквивалентно, матричного уравнения (17). При большой размерности n базиса последняя операция достаточно трудоемка. Если выбрать такие базисные функции, которые в пространстве H ортогональны между собой попарно, то есть
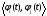 =
=
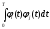 = 0; (1.18)
= 0; (1.18)
i
= 1…n;
j
= 1…n
; i
 j
,
j
,
то матрица U становится диагональной, а система (9) – разрешенной. Разложение по ортогональному базису при возможности увеличения размерности базиса до бесконечности и выполнении некоторых других условий называется обобщенным рядом Фурье [1]. Простота решения системы уравнений (9) в большинстве случаев определяет использование ортогональных базисов (обобщенных рядов Фурье), в том числе и тригонометрических. Однако, в некоторых задачах предпочтение может быть отдано неортогональным разложениям. Степень гладкости разлагаемой функции можно характеризовать порядком R младшей производной, в которой на интервале разложения существуют разрывы первого рода (конечные разрывы). Известно [2], что сходимость тригонометрического ряда Фурье, под которой понимается уменьшение коэффициентов ряда с ростом его номера, имеет порядок 1/nR. Однако, при сколь угодно высокой степени гладкости разлагаемой функции внутри интервала разложения, несовпадение значений разлагаемой функции в начале и конце интервала разложения эквивалентно разрыву в функции, что приводит к весьма слабой сходимости ряда порядка 1/n. Это является следствием периодичности ортогонального тригонометрического базиса на интервале разложения. Возможность улучшения сходимости за счет отказа от ортогональности базиса проиллюстрируем простым примером. Разложим функцию f(t) = exp(-t) на интервале (0…2) по базису:
1, cos(pxt), sin(pxt), cos(2pxt),sin(2pxt), … cos(qpxt),.. (1.19)
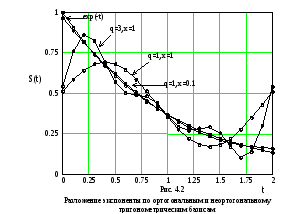
Здесь q – число гармоник в базисе. Базис (19) ортогонален при x = 1. Отличие величины x от единицы характеризует удаление базиса от условий ортогональности. На рис.1 представлена зависимость от x среднеквадратической ошибки разложения
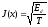
для базисов различной размерности: q = 1, q = 2, q = 3.
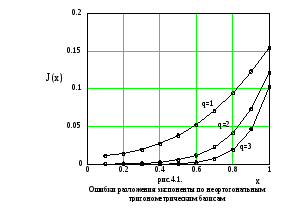
На Рис.2 представлены графики разлагаемой функции, разложения по ортогональным базисам различных размерностей (кривые q = 1, q =2, q = 3) и по неортогональному базису размерности q = 1 (кривая x = 0.1). Из графиков, представленных на рисунках 4.1 и 4.2, можно видеть, что увеличение размерности ортогонального базиса не приводит к существенному уменьшению ошибки разложения. Применение же неортогонального базиса позволяет существенно уменьшить ошибку разложения уже при малой размерности базиса. Увеличение объема расчетов на решение уравнений (17) может компенсироваться увеличением точности разложения.
1.3. Разложение дискретных функций
Экспериментальные данные обычно являются дискретными
Функциями времени, то есть представляют собой набор
Отсчетов:
f(tj) = f(j); j = 1…N.
Для разложения дискретных функций базисные функции и само разложение также должны быть дискретными:
фi(tj)
= фi(j),
S(j) =
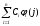 ,
i = 1…n, j = 1…N
,
i = 1…n, j = 1…N
Функциональное пространство H, введенное выше, становится N – мерным, а скалярное произведение определяется соотношением:
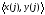 =
=
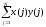
Энергия ошибки (4) (минимизируемый критерий) имеет вид:
Ed
=
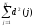 =
=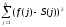
Уравнения (9) и (17) для определения оптимальных коэффициентов разложения остаются в силе, но в параметрах Ui,k и Vi интегралы заменяются суммами:
Ui,k
=
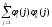 ;Vi
=
;Vi
=
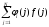 (1.20)
(1.20)
