1.5. Оценка уровня помех в обрабатываемой реализации

При обработке экспериментальных реализаций представляет интерес уровень помех, присутствующих в этих данных. Для сигналов, которые можно представить в виде зашумленных сигналов (21), можно оценить амплитуду помехи (а). Из соотношений (24) – (26) можно выразить амплитуду помехи, присутствующую в эксперименте:

a² = E_d/(E_h – E_sh ) = E_d/E_h(1 – К_ф²)

Энергия ошибки разложения E_d вычисляется в процессе разложения обрабатываемой реализации. Величины E_h, E_sh, и К_ф оцениваются выражениями (27), (39) и (40). Таким образом:

a² = E_d/D_h(N – n) (1.41)

Напомним, что здесь D_h – дисперсия шума, N – число отсчетов в обрабатываемой реализации, n – количество базисных функций.

1.6. Оценка погрешностей разложения

Для зашумленных сигналов типа (21) в качестве погрешности dS(j) разложения естественно принять разность между разложением S(j) зашумленного сигнала и идеальным (незашумленным) сигналом S₀(j).

Учитывая выражения (21) и (22) можно записать:

dS(j) = S(j) – S₀(j) =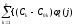=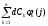(1.42)

Здесь dC_k = C_k – C_0k – погрешности разложения в области параметров сигнала.

Из рассмотрения треугольника a0a1a3 (рис.3) можно получить:

dS(j) = S(j) – S₀(j) = аS_h(j) (1.43)

Вектор аS_h(j) был определен выше, как проекция помехи на базисную гиперплоскость S_n, амплитуда помехи а оценивается соотношением (41).

На Рис.4 представлен треугольник а0а1а3 из Рис.3, расположенный в базисной гиперплоскости S_n. При обработке экспериментальных данных вектор S(j) становится известным, вектора же S₀(j) и аS_h(j) – неизвестны. Однако длина L вектора aS_h(j), характеризующего ошибку разложения, может быть оценена с помощью соотношений (39), (40),(41):

L = a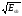= = 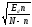К_ф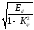 (1.44)

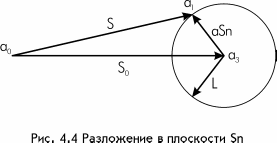
На Рис.4.4 приведена окружность (в общем случае гиперокружность) с центром в точке а3 и радиусом L (44). Истинное положение точки а3 (конца вектора S₀(j)) лежит на

упомянутой окружности, что и является оценкой погрешности разложения.

Сравнивая соотношения (42) и (43) можно получить:

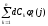= a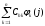(1.45)

Отсюда

dC_k = aC_hk , k = 1…n. (1.46)

Уравнения (46) показывает, что статистические характеристики ошибок коэффициентов разложения C_k могут быть оценены по статистическим характеристикам коэффициентов C_hk разложения шума. Дисперсию C_hk с учетом (31) можно записать:

D[C_hk] = M[C_hk ²] =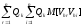 (1.47)

Подставив сюда (36), получим:

D[C_hk] = D_h 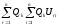(1.48)

Внутренняя сумма в (48) является элементом единичной матрицы в силу (31) , поэтому:

Отсюда и из (48)

D[C_hk]=D_hQ_kk (1.49)

Таким образом, дисперсию ошибок вычисления коэффициентов разложения сигналов типа (21) можно выразить из (46) и (49) следующим образом:

D[dC_k]=a²D_hQ_kk (1.50)1.7. Численная оптимизация по параметрам базиса

В некоторых приложениях, когда обрабатываемый сигнал может быть представлен в виде суммы известных функций, как (21), известен только вид этих функций, но неизвестны некоторые их параметры. Так, при обработке частотных характеристик динамических звеньев, известно, что обрабатываемые сигналы являются гармоническими, однако частоты этих сигналов могут быть неизвестными, или известными с недостаточной точностью. При обработке звуковых (речевых) сигналов частоты колебательных составляющих неизвестны. В таких случаях обрабатываемый сигнал (21) можно представить в следующем виде:

f(j) = S₀ (j) + ah(j) , S₀ (j) = 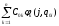, (1.51)

i = 1…m , j = 1…N

В качестве базисной системы функций для разложения сигнала (51) естественно принять

ф₁(j,q_i), ф₂(j,q_i) …ф_m(j,q_i) , i = 1…m. (1.52)

Здесь q_i – неизвестные параметры базисных функций, m – число этих параметров. Задав произвольную совокупность параметров q_i, i = 1…m, произведем разложение сигнала (51) по базису (52), используя соотношения (17) и (20). В результате получим набор коэффициентов разложения и энергию ошибки, которые являются функциями принятой совокупности параметров q_i:

C_k = C_k(q₁…q_m) , E_d = E_d(q₁…q_m) (1.53)

Произведя численную оптимизацию E_d(q₁…q_m) по параметрам q_i, i = 1…m, получим:

C_k ^опт = C_k ^опт(q₁^опт…q_m^опт), E_d^опт = E_d^опт(q₁^опт…q_m^опт) (1.54)

Оптимальные параметры из (54)

q_i^опт , i = 1…m, C_k ^опт, k = 1…n, (1.55)

являются оценками параметров q_0i , i = 1…m , и С_0k , k = 1…n незашумленного сигнала (51).