Мкч с использованием представления о наклонных секущих

Покажем особенности представления неявной расчетной схемы второго порядка точности. Поскольку вычисления ведутся по возрастающим номерам ячеек последовательно для эйлерова, лагранжева и заключительного этапов, при расчете i-ячейки перед эйлеровым этапом известными являются не только все параметры в центрах всех ячеек вnмомент времени, но и промежуточные параметры, , где Х = (р, u) и Y = (p, v). Тогда можно выразить значения параметров на дробном шагеt^n+1/2на границахi-1/2,j,i,j-1/2 и давление в центреi-ячейки с использованием представления о наклонных секущих (рис.2.5):

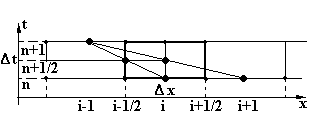
Рис.2.5. Представление о наклонных секущих

; (2.70)

; (2.71)

. (2.72)

Тогда формулы для промежуточных скоростей записываются в виде:

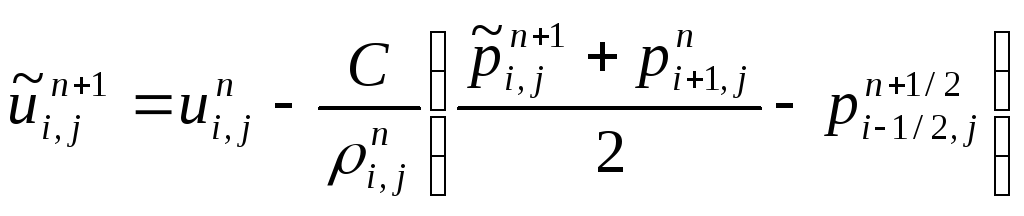; (2.73)

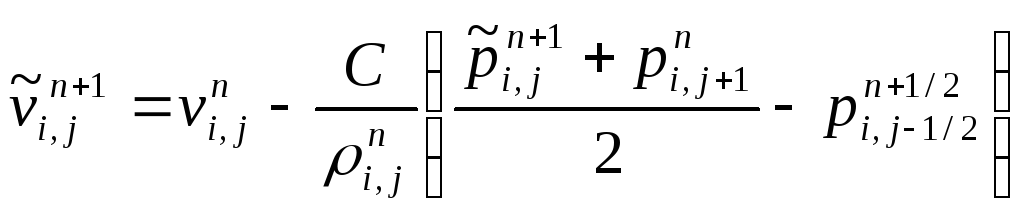. (2.74)

После соответствующих преобразований уравнение полной энергии эйлерова этапа (2.54) заменяется уравнением внутренней энергии. Для простоты запишем без диссипативных членов в правой части:

.

Поскольку е = с_vT=p/(k-1), то при=constэйлерова этапа получим

. (2.75)

Данная форма уравнения энергии используется и в методе частиц в ячейках Харлоу. В конечно-разностной форме это уравнение имеет вид:

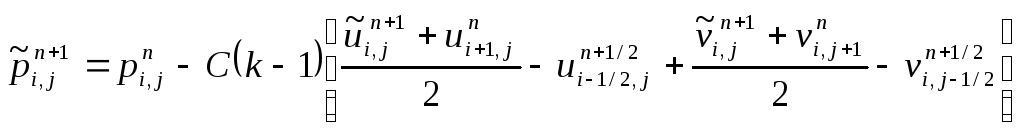. (2.76)

После подстановки (2.73) и (2.74) в уравнение (2.76) и соответствующих преобразований,  получается аналитическое выражение для определения промежуточного давления без каких-либо итераций.

(2.77)

Найденное по этой формуле значение давления подставляется в (2.73) и (2.74) для вычисления промежуточных скоростей. Завершается эйлеров этап расчетом полной энергии:

. (2.78)

Расчетные соотношения (2.73), (2.74) и (2.77) соответствуют представлению о неявной схеме, поскольку в них используются параметры как n, так и n+1 временного слоя. Далее в обычной последовательности МКЧ выполняются лагранжев и заключительный этапы, осуществляется переход к расчету i+1,j или i,j+1 ячеек.

Применение предложенной схемы позволяет при сохранении устойчивости вычислений увеличивать сеточное число Куранта до значений 0,4 - 0,8 даже при моделировании течений с большими градиентами параметров, характерных для затопленных струй, т.е. увеличивать точность результатов и значительно сокращать время маршевого счета.

Наличие в составе расчетных соотношений (2.59) – (2.61) диссипативных членов, отражающих вязкость и теплопроводность, значительно повышает устойчивость расчетов, и, несмотря на громоздкость выражений, позволяет уменьшить время вычислений при решении стационарных задач на установление процесса за счет повышения сеточного числа Сu.

Лекция №6. Метод Распада Произвольного Разрыва (Линеаризованный)

Наиболее универсальными с точки зрения организации расчета нестационарного течения являются конечно-разностные методы, использующие фиксированную сетку в системе координат расстояние – время. К ним относится, в частности, метод распада произвольного разрыва (МРПР), основные положения которого разработаны  С.К.Годуновым.

МРПР, как и другие численные методы газовой динамики, опирается на систему базовых интегральных уравнений, выражающих основные законы сохранения – массы, импульса (количества движения) и энергии:

; (215)

; (216)

. (217)

Здесь: х, t- система координат расстояние-время,р, ρ, Т, v, R, c_p, c_v, е = u+v²/2, λ_т, α_w, T_с, D- соответственно давление, плотность, температура, скорость потока, газовая постоянная, изобарная и изохорная теплоемкости, удельная энергия (сумма отнесенных к единице массы внутреннейu = c_vТ, и кинетическойv²/2энергий),коэффициенты трения и теплоотдачи в стенку канала, температура стенки канала и гидравлический диаметр канала (в случае круглого трубопровода равен его внутреннему диаметру).

В данной постановке принимается физическая модель термодинамически идеального и совершенного газа (p = RT, c_p = соnst, с_v = соnst, R = c_p - c_v = c_v(к-1), для воздуха c_p = 1005,55 Дж/(кг·К), с_v = 718,25 Дж/(кг·К), R = 287,3 Дж/(кг·К), к = 1,4) без воздействия внешних сил и источников тепла. Для учета диссипативных явлений используются представления Дар­си-Вейсбаха (вязкое трение) – правая часть уравнения (216) и Ньютона (теплоотдача в стенки канала) – правая часть уравнения (217).

При моделировании течения холодного воздуха (впускной тракт) теплообменом со стенками можно пренебречь, и правая часть уравнения (217) принимается равной нулю. В первом приближении расчетов можно также отказаться и от учета трения – принять равной нулю и правую часть уравнения (216).

Для организации расчета трубу длиной L разбивают на mотрезков. Тогда шаг расчета по координате х, т.е. линейный размер x расчетной ячейки составит

. (218)

Необходимо также выбрать шаг расчета по времени t.Расчет будет устойчивым, т.е. выполняться без сбоев,если при выборе t будет выполнено условие для так называемого сеточного числа Куранта Со:

, (219) где а₀ – начальная скорость звука. Для нормальных условий с холодным воздухом:

= 347,4 м/с.

Как правило, для обеспечения устойчивости расчета описываемой модификацией метода выбирают Со = 0,5-0,6. Тогда для шага по времени при расчете течения воздуха будем назначать:

. (220)

Теперь можно выстроить ортогональную расчетную сетку из mячеек по горизонтали (по осих) иNячеек по вертикали (по осиy) (рис.41). Ячейки в горизонтальных рядах нумеруются:х₁, х₂, ..., х_i, ..., х_m.Границы ячеек нумеруются дробными индексами, например, для правой границыi– ячейки имеемх_i+1/2. Число ячеек по вертикали получится автоматически, если назначить окончание времени расчетаt_N:

. (221)

Расчетные параметры снабжаются также и верхними индексами, соответствующими временным слоям сетки. Эти индексы меняются в интервале 0,..., n,...,N, тогда, например, если имеем, то это давление вi– ячейке в момент времениtⁿ .

Для организации расчета должны быть заданы начальные (НУ) и граничные условия (ГУ).

В качестве НУ необходимо назначить распределение всех расчетных параметров по всем ячейкам m ячейкам первого временного рядав момент времениt⁰ = 0.

Например: v⁰₁=... v⁰_i ...= v⁰_m = 0 м/с, р⁰₁=... р⁰_i ...= р⁰_m = 100000 Па, Т⁰₁=... Т⁰_i ...= Т⁰_m = 300 К,  = p/RT = ρ⁰₁=... ρ⁰_i ...= ρ⁰_m = 1,160 кг/м³.

В качестве ГУ слева, т.е. в начале координат, будем рассматривать открытый конец со скруглением, которое обеспечивает втекание в трубу без потерь. Тогда, считая процесс адиабатным и не прибегая к ГДФ, можно воспользоваться уравнением энергии. И если в объеме слева имеем давление р_а = р_а* и температуру Т_а = Т_а*, для связи со скоростью и давлением втекания будет справедливо:

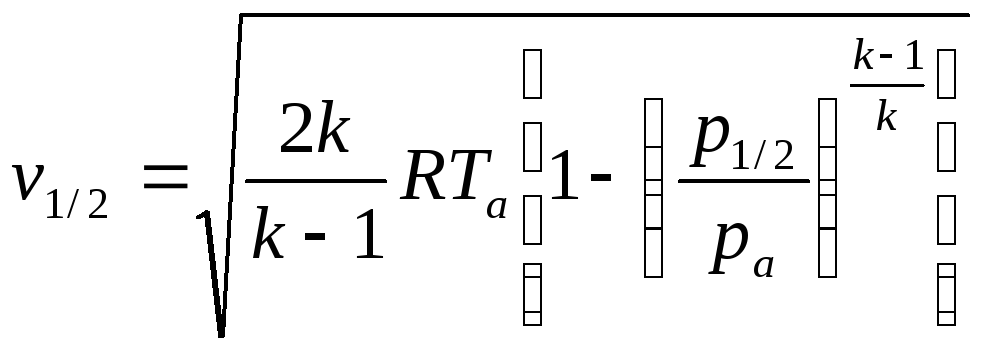. (222)

Соответственно для температуры и плотности:

; (223)

. (224)

В качестве ГУ справа, т.е. в конце трубы, будем рассматривать либо открытое проходное сечение, когда давление на границе равно давлению в полости истечения, в простейшем случае – атмосферному:

, (225) либо закрытый конец, когда скорость на границе полностью затормозится, т.е. станет равной нулю:

. (226)

Расчет выполняется последовательно от 1  до m ячейки. Сначала для всех ячеек определяются объемные параметры в исходный (начальный) момент времени t⁰ = 0: полная (т.е. не удельная) масса

, (227)

полное количество движения

, (228)

и полная энергия

. (229)

Если принять единичное значение площади Fпроходного сечения трубы, то в качестве объема ячейки можно принять ее линейный размер, т.е. шаг по длине

. (230)

В общем случае параметры v⁰_i, р⁰_i, Т⁰_i , ρ⁰_i и, соответственно, объемные параметры М⁰_i, К⁰_i, Е⁰_i могут быть во всех ячейках ряда различными, т.е. будем иметь дискретное распределение параметров по длине трубы. Тогда труба может быть представлена в виде отдельных объемов Δх, заполненных газом с разными параметрами, и которые по границам разделены перегородками (мембранами).

Таким образом, имеющееся на практике гладкое распределение параметров по длине заменяется разрывным, на каждой из границ имеется произвольный разрыв параметров.

В каждый из расчетных моментов времени tⁿ, в том числе и в начальный момент, когдаtⁿ = t⁰ = 0, происходит как бы мгновенное разрушение всех мембран. В результате на границах между ячейками (дискретными объемами) происходят распады произвольных разрывов (РПР). На каждой из границ образуются две элементарных волны, фронты которых распространяются один —вдоль С⁺ ‑характеристики, идущей от точки разрыва (границы) вправо вперед, другой —вдоль С^- ‑характеристики, идущей от точки разрыва влево назад (рис.2).

Если, например, давление в i- ячейке вn- момент времени было больше давления вi+1- ячейке, а скорости были равны нулю, то в этот момент времени от границыi+1/2 влево, внутрь ячейкиi, пойдет волна разрежения, а вправо, внутрь ячейкиi+1, - волна сжатия.

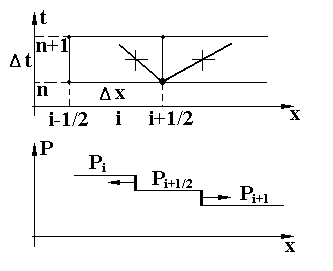
Рис.42. Образование элементарных волн при РПР

В соответствии с теорией нестационарного течения, при переходах через фронты элементарных волн выполняются законы сохранения инвариантов Римана. Так при переходе через фронт, идущий слева направо, т.е. вдоль С⁺ характеристики, будет оставаться постоянным инвариант Римана r^- с выполнением соотношения

. (231)

При переходе же через фронт, идущий справа налево, т.е. вдоль С^- —характеристики, будет оставаться постоянным инвариант Римана r⁺ с выполнением соотношения

. (232)

В конечных разностях будем иметь соответственно:

; (233)

, (234)

где

- (235)

осредненное значение произведения плотности и скорости звука для решения задачи РПР наi+1/2границе.

Из системы уравнений (233)-(234) легко выразить «потоковые» давление и скорость через границу i+1/2при РПР:

; (236)

. (237)

Для определения потоковой плотности используются зависимости

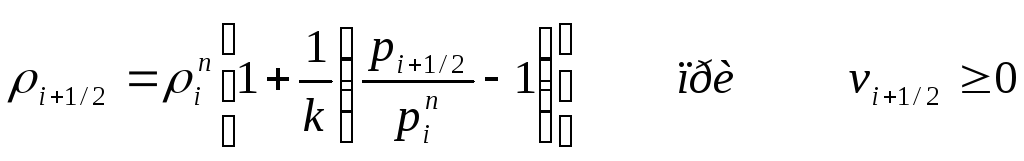; (238)

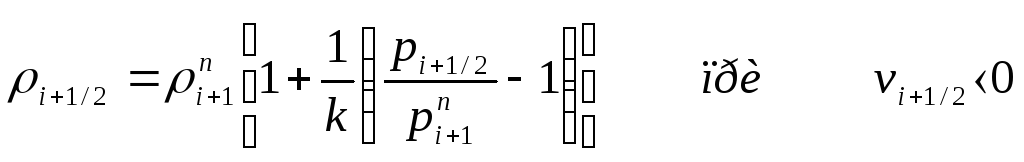, (239)

которые представляют собой линеаризацию адиабатных соотношений.

Для расчета на левой границе из (233) будем иметь:

. (240)

Поскольку с другой стороны имеется формула (222) для расчета скорости через границу, приравнивая (222) и (240), получим расчетное уравнение

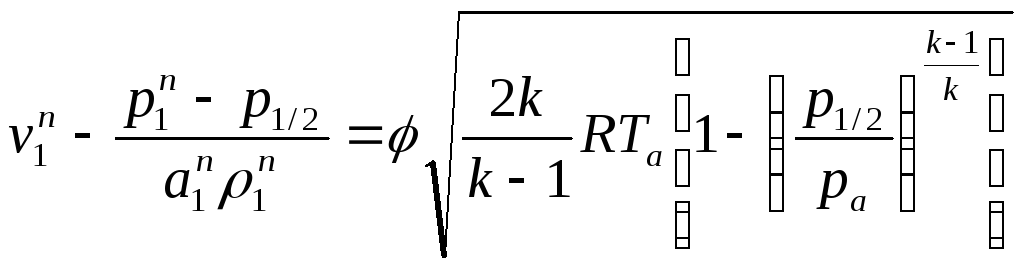. (241)

Решая его одним из методов последовательных приближений (практика показала, что надежнее всего использовать метод деления отрезка пополам), находим давление p_1/2  втекающего через границу газа. Затем по формуле (240) найдем соответствующую скорость, по формулам (223) и (224) – температуру и плотность.

Рассмотрим правую границу, где последняя ячейка расчетной области будет иметь индекс m, а узел непосредственно на границе - m+1/2. При РПР на этой границе налево вдоль С^-- характеристики пойдет элементарная простая волна, при переходе через фронт которой инвариант r⁺ остается постоянным, и из уравнения (234) можно получить в конечных разностях:

. (242)

Если конец трубы закрыт, то, очевидно, v_m+1/2 = 0. Это положение позволяет определить давление на границе:

, (235)

Затем:

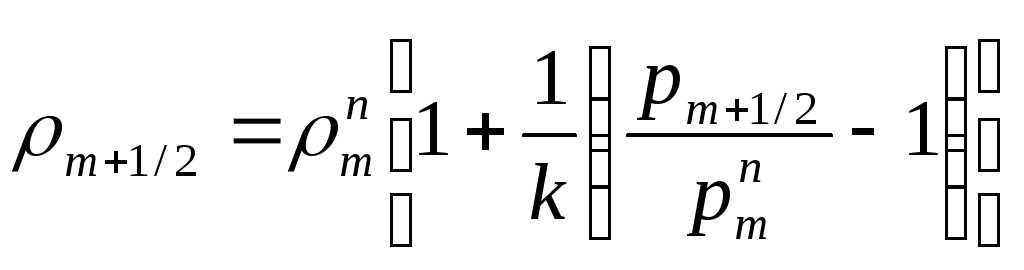. (236)

Здесь также можно отметить, что формула (235) отражает тот факт, что при подходе к закрытому концу волны сжатия (т.е. когда в данном случае v_m > 0) давление на границе в результате РПР возрастает, а при подходе волны разрежения (v_m < 0) упадет ниже первоначального р_mⁿ.

Пусть труба справа открыта, и происходит истечение. Тогда (225), и при подстановке в (234) получим скорость истечения:

, (237)

откуда видно, что при подходе волны сжатия (p_m > p_а) скорость истечения v_m+1/2, направленная по оси координат х, превзойдет скорость v_m.

Для плотности будем иметь:

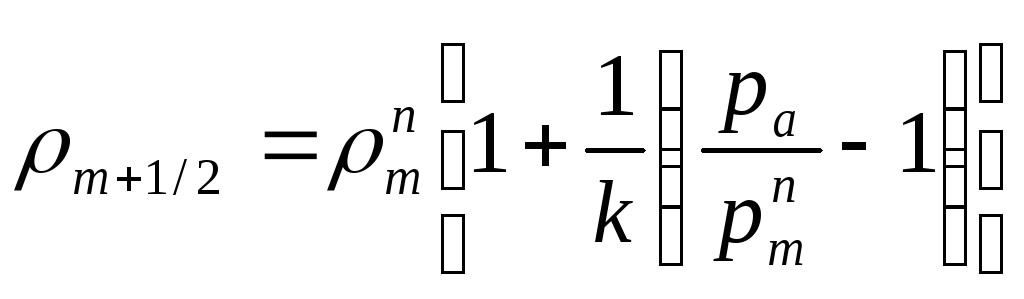. (238)

Обратимся теперь к исходным интегральным уравнениям (215)-(217). Решая задачу без диссипативных членов, т.е. без правых частей, отметим, что левые части представляют собой интегралы по контуру. И в конечных разностях для каждой из ячеек представляют собой сумму объемных параметров, полученную при обходе ячейки по ее прямоугольному контуру против часовой стрелки. Тогда можно записать:

; (239)

; (240)

. (241)

Эти уравнения показывают, что в трубе с единичной площадью проходного сечения объемныепараметры: полная масса газа, полное количество движения и полная энергия объеме i ‑ ячейки за расчетный шаг по времени t, т.е. между tⁿ и tⁿ⁺¹  временным слоями численного расчета изменяются за счет потоковых параметров на левой (i‑1/2) и правой (i+1/2) границах ячейки. Т.е. при положительном значении скоростей через левую границу прибудет массаМ_i-1/2 = (ρv)_i-1/2Δt, количество движенияК_i-1/2 = (Мv)_i-1/2и энергияЕ_i-1/2 = (Ме)_i-1/2, через правую границу произойдут соответствующие вычитания М_i+1/2 =(ρv)_i+1/2Δt, К_i+1/2 = (Мv)_i+1/2 и Е_i+1/2 = (Ме)_i+1/2.

Кроме этих составляющих на изменение количества движения по сравнению с исходным значением окажет влияние положительное воздействие импульса силы давления на левой границе I_i-1/2 = p_i-1/2Δt и отрицательное - воздействие импульса силы давления на правой границе I_i+1/2 = p_i+1/2Δt. На изменение энергии по сравнению с исходным значением окажет влияние положительная работа, совершенная силой давления на левой границе L_i-1/2 = (pv)_i-1/2Δt, и отрицательная работа, совершенная силой давления на правой границе L_i+1/2 = (pv)_i+1/2Δt.

После определения объемных параметров М, К и Е в n+1 момент можно определить и основные газодинамические параметры в этот момент:

; (242)

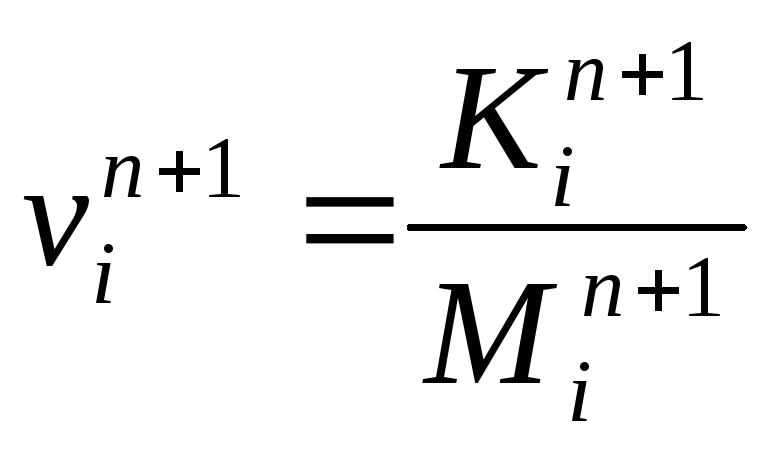; (243)

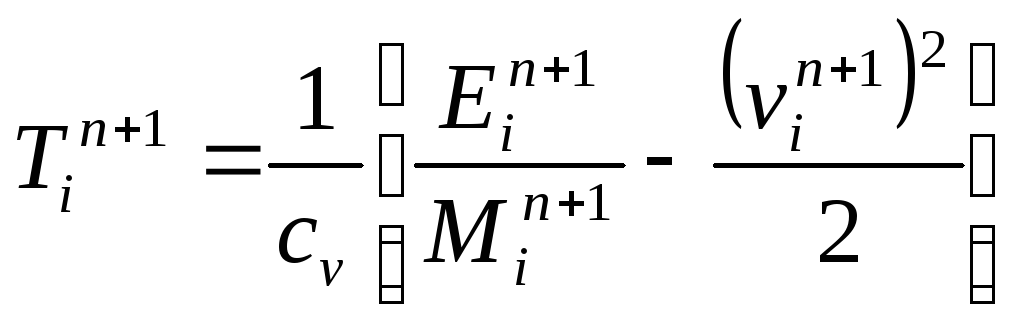; (244)

. (245)

Очевидно, из последних двух формул можно выразить непосредственно:

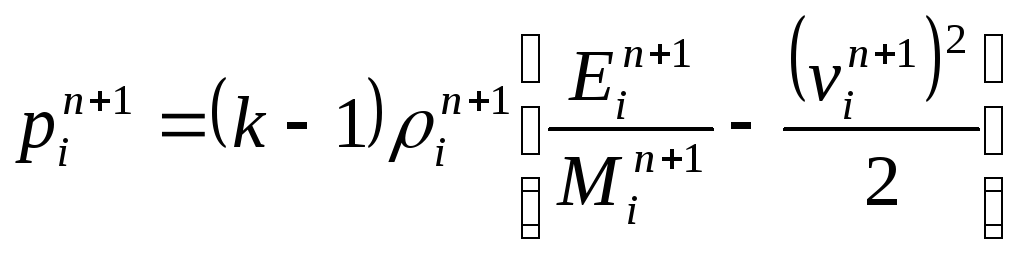. (246)

После завершения расчета по всем i– ячейкам ряда, необходимо перейти к следующему временному слою, заменив верхние индексыn+1 всех параметров наn, и так далее, переходя к последующим рядам вплоть до окончания назначенного расчетного времениt^N.

Расчет временного ряда начинается с определения потоковых параметров при входе через левую границу (241), (240). Далее следует расчет внутри расчетной области по формулам (236), (237), (238) или (239) по всем i, наконец, правая граница (235), (236), если конец закрыт, и (237), (238), если конец трубы открыт. Затем определение объемных параметров:

; (247)

; (248)

, (249)

где . (250)

Расчет может быть организован вообще без использования температуры. Поскольку ,

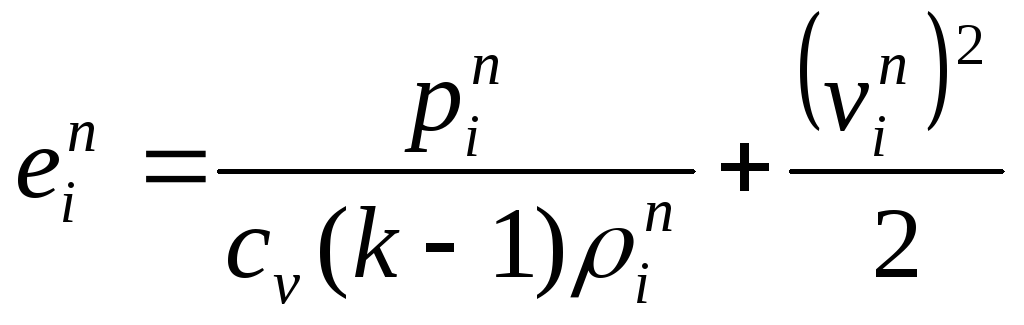. (251)

Затем следует повторение балансовых расчетов (239)-(241).