Используемые программы

• Существует большое число программных продуктов, как коммерческих, так и некоммерческих.

• Всех их можно условно разделить на универсальные и специализированные

• Специализированные коды предназначены для решения какой-нибудь узкой задачи. Универсальные, соответственно, могут быть применены в любой отрасли

• К наиболее распространенным коммерческим универсальным кодам можно отнести: Star-CDFluentFireCFXKiva– отличается направленностью к ДВС Кроме того стоит упомянуть: FlowVision – отечественная разработкаOpenFOAM– наиболее развитыйopensourceпроект

Лекция №2. Базовые уравнения и модели газа

• Рождественский, 133

• Уравнение состояния

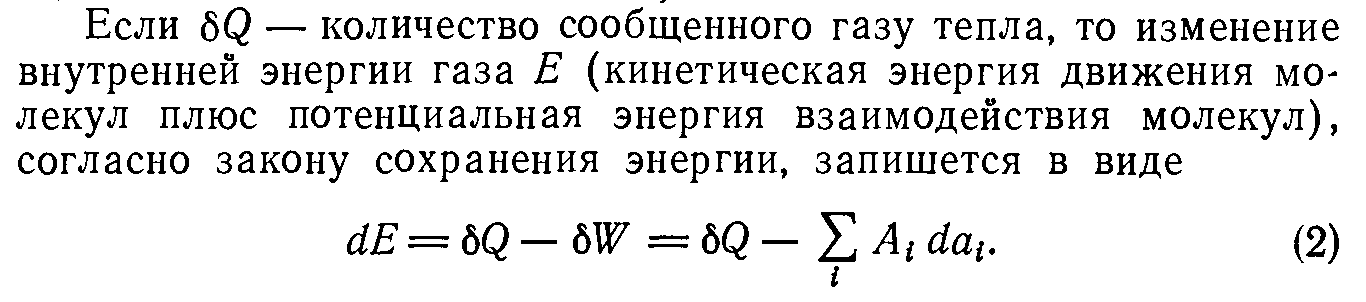
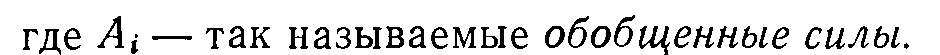
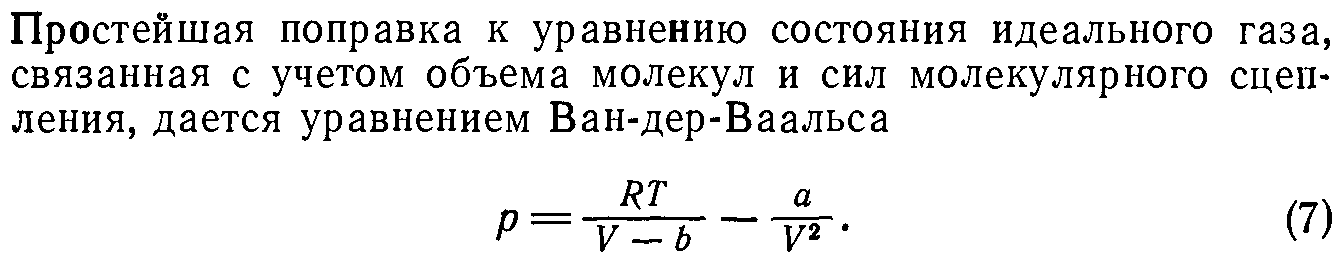
• Оран, 39

• Рождественский, 140

• Уравнение неразрывности

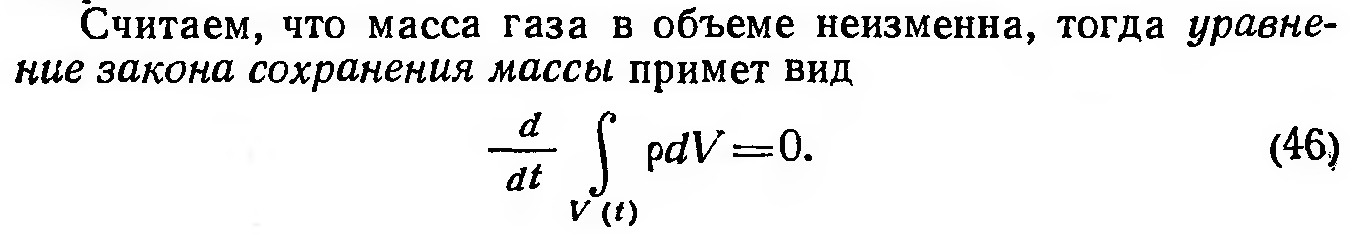
• Уравнение Навье-Стокса

• Замечание по поводу давления:

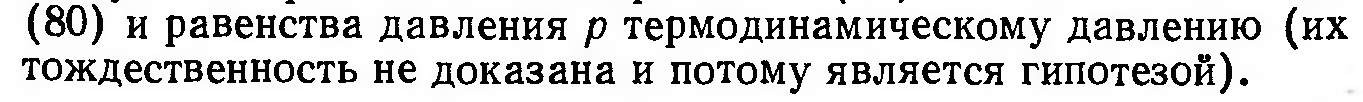
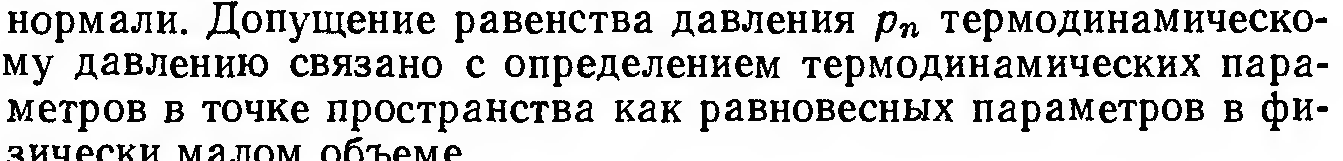
• Уравнение Эйлера – уравнение количества движения сжимаемой жидкости для невязкого газа. Допущение приемлемо, например, для хорошо текучих газов – гелия, водорода и т.п., но не во всех случаях (Двигатель, 39)

• Уравнение энергии

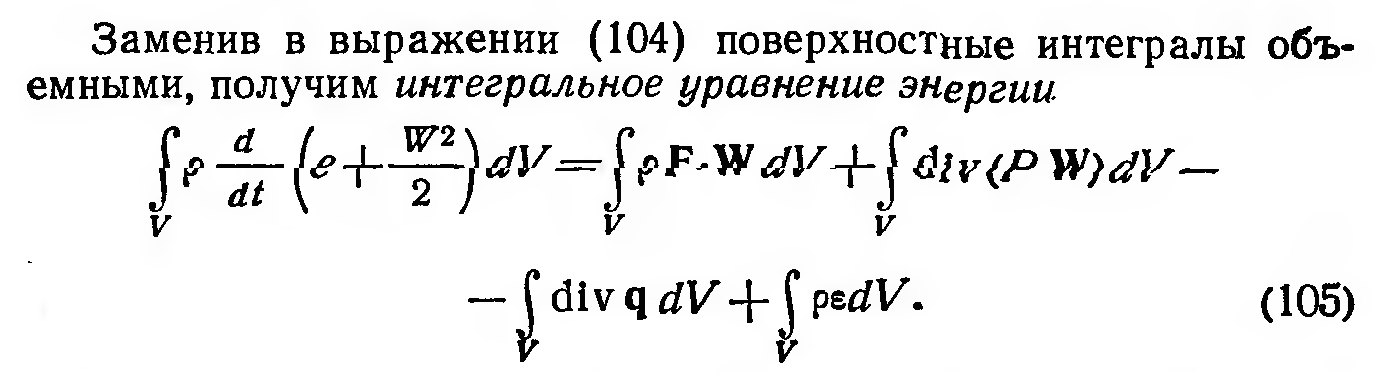
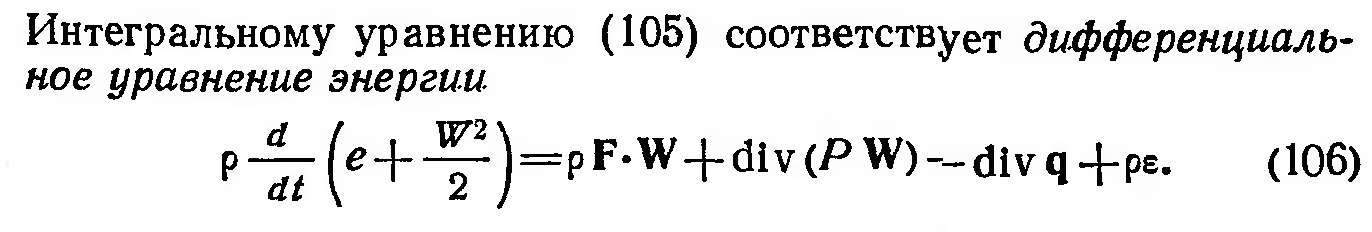
• Кроме того, при расчете течений может возникнуть необходимость учета других физических факторов, таких как: - Химические реакции; - Турбулентность (будет рассмотрена особо); - Поверхности раздела сред; - Наличие дисперсных частиц в потоке; - Радиационный теплообмен; - Диффузионные явления; - и т.д.

Лекция №3. Основы численных методов

• Оран, 45

• Стационарная (детерминированная) задача Андерсон, 22

• Андерсон, 26 Нестационарная

• Андерсон, 39

• Самарский, 104

• Андерсон, 60

• Андерсон, 59

• Андерсон, 61

• Погрешности Андерсон, 61

• Самарский, 95

• Как правило, верхний индекс обозначает шаг по времени, а нижние – координаты ячейки/узла

• Оран, 105

• Оран, 106

• Самарский, 112

Лекция №4. Метод конечных разностей

• Разностный метод был, пожалуй, первым из тех, что применялись для численного решения уравнений. Впервые он был применен Эйлером около 1768 года.

• Самарский, 95

• Теоретически переход от дифференциальных уравнений к алгебраическим обосновывается разложением функции в ряд Тэйлора:

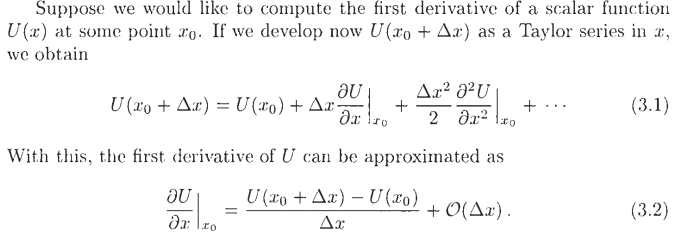
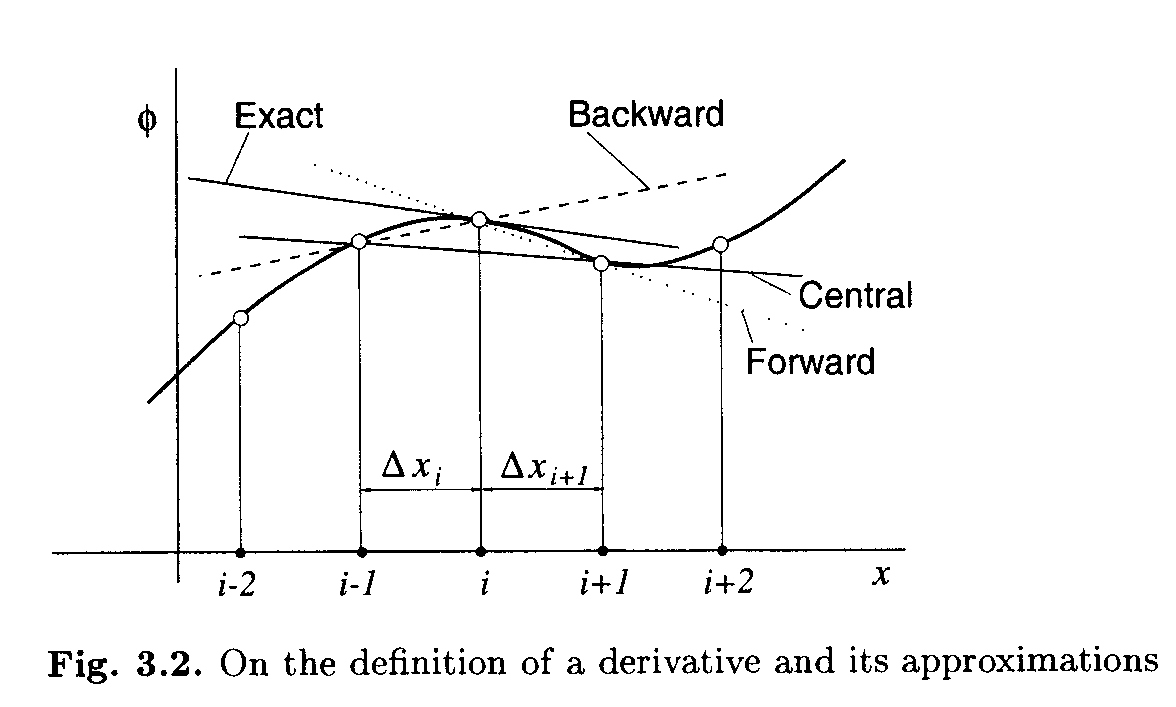
• Способ представления частных производных может быть различным, в зависимости от него для одной и той же задачи может существенно варьироваться точность решения и устойчивость вычислений.

• Ferziger, 41

Разностные схемы

• Рождественский, 427

• Явные разностные схемы обычно неэкономичны, так как для соблюдения условия устойчивости требуют малого шага по времени

• Простейшие шаблоны неявных разностных схем: Круглов, 221-223.

Разностные схемы с пересчетом или «предиктор-корректор»

• Круглов, Меднов, 226

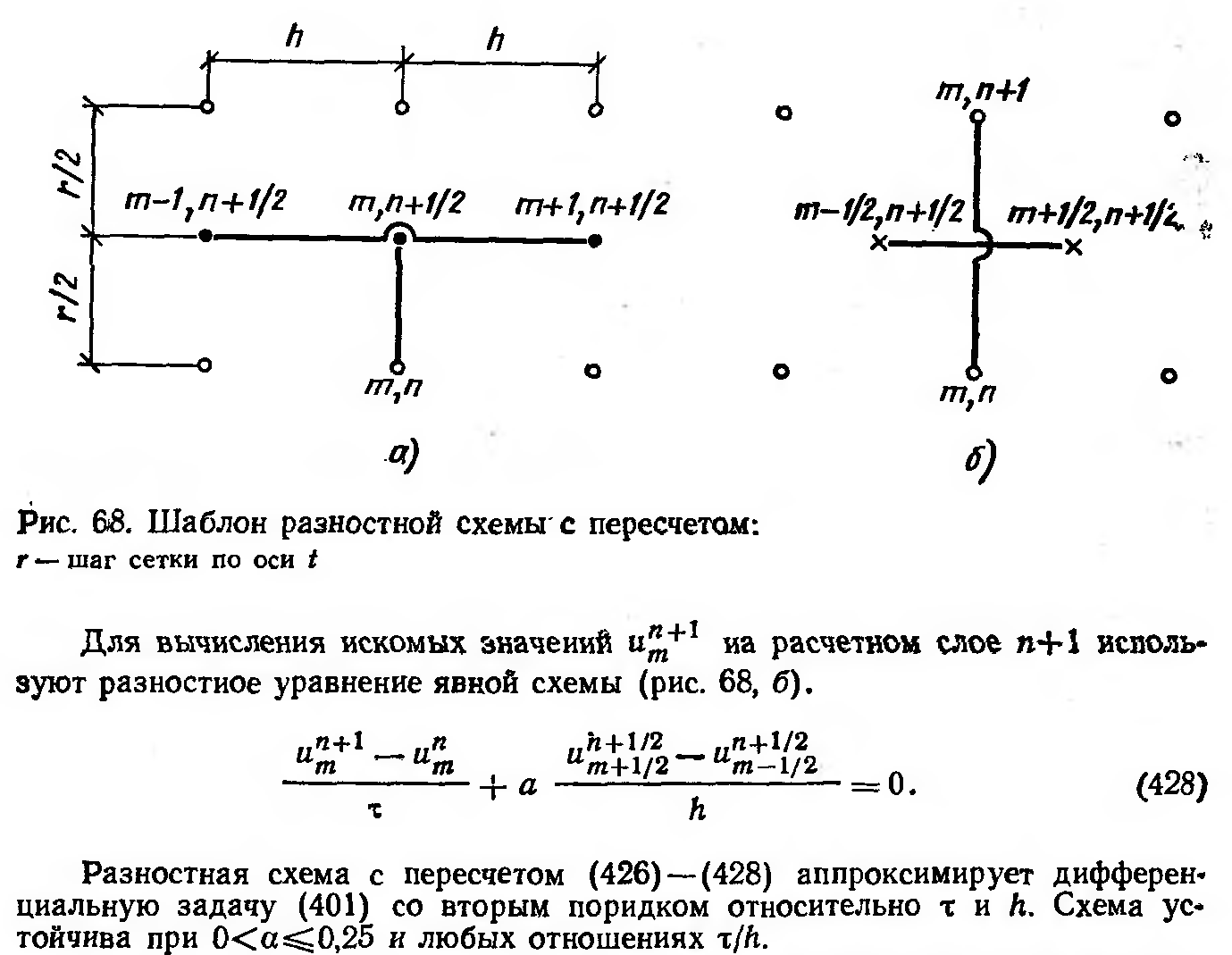
Консервативные разностные схемы

• Круглов, Меднов, 227

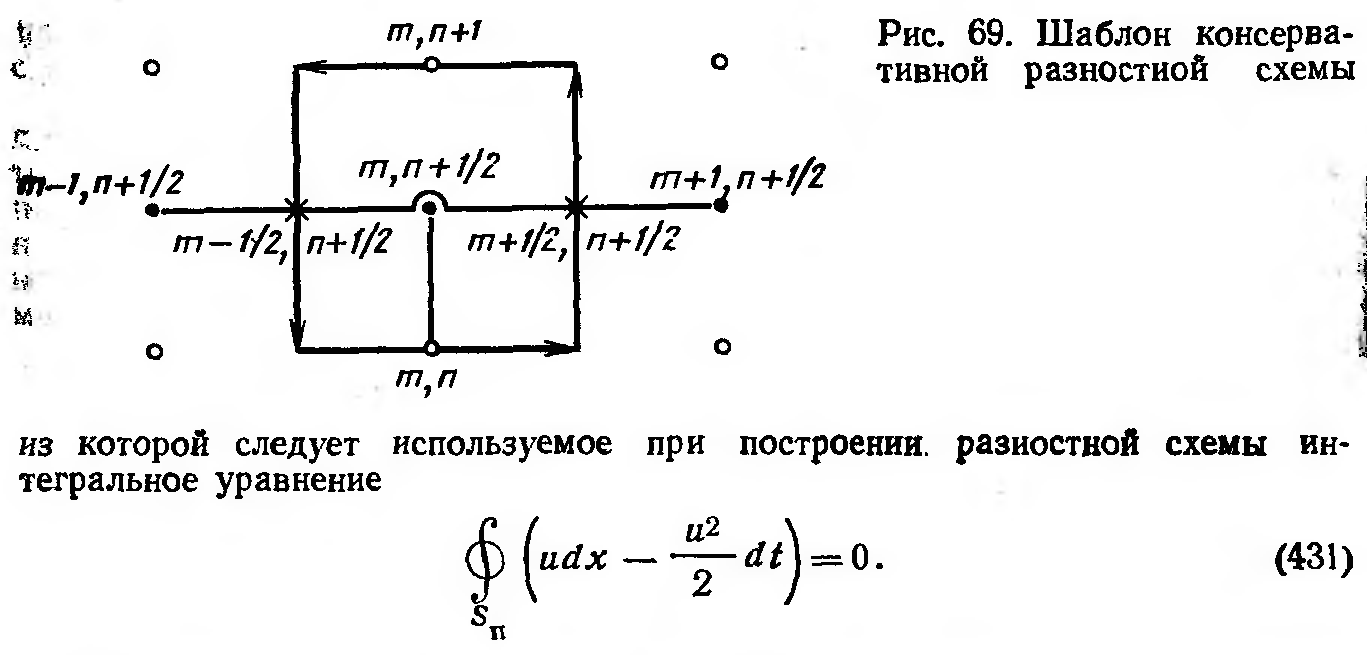
Метод интегрирования «Чехарда»

• Оран, 182-183

Методы Лакса-Вендрова

• Оран, 300-302

Методы Рунге-Кутты

• Мак-Кракен – Численные методы и программирование на фортране, стр. 397-404, 406-407, 409

Заключение

• Главное достоинство метода конечных разностей – простота

• Еще одним важным преимуществом является возможность легко получить высокий порядок аппроксимации, и, следовательно, достичь высокого порядка точности пространственной дискретизации. С другой стороны его использование ограничено необходимостью применения структурированной сетки

• 

Лекция №5. Метод Крупных Частиц

Базовый МКЧ

МКЧ был разработан О.М. Белоцерковским и  Ю.М.Давыдовым. И является модификацией метода частиц в ячейках Харлоу. Метод позволяет моделировать затопленные струи, отрывные зоны, различного рода турбулентные пульсации а также другие особенности внешнего и внутреннего стационарного и нестационарного течений.

Важными особенностями МКЧ являются простота и универсальность реализации, не требующая построения функциональных адаптивных сеток, а также простота алгебраической записи численных алгоритмов.

Рассмотрим расчетные соотношения МКЧ. Дифференциальные уравнения законов сохранения в дивергентной форме можно записать в виде: (здесь u=v_x,v=v_y)

= 0; (2.51)

; (2.52)

; (2.53)

. (2.54)

Система дополняется уравнением состояния газа в виде

,

где ,- удельная внутренняя энергия.

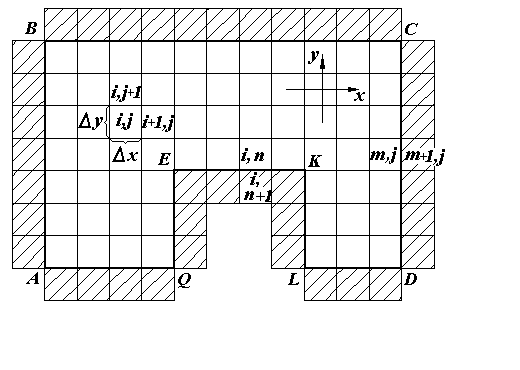
Для расчета область моделирования покрывается эйлеровой расчетной сеткой в системе координат x-yс фиксированными прямоугольными ячейками со сторонамиx,y. Для простоты и универсальности вычислений целесообразно принятьx=y=s(рис.2.4). Выбрав значения шагов по пространству, следует назначить шаг по времениt. При этом необходимо руководствоваться значением сеточного числа Сu= аt/s1. Для выполнения устойчивых вычислений необходимо выбирать такой шаг по времени, чтобы Сu= 0,05-0,10.

Опишем теперь отдельные этапы расчета, соответствующие представлению о расщеплении по физическим процессам.

Для расчета на первом, эйлеровом этапе не учитываются эффекты переноса, т.е. div() = 0, где= {1,u,v,E}. В результате из уравнения неразрывности (2.51) получается

, (2.55)

т.е. плотность на данном этапе остается постоянной, и ее значение в уравнениях (2.52 –2.54) можно вынести из-под знака дифференциала в производной по времени. Преобразуя и раскрывая правые части, получим:

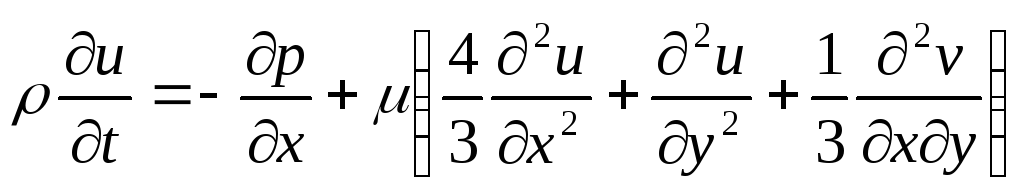; (2.56)

; (2.57)

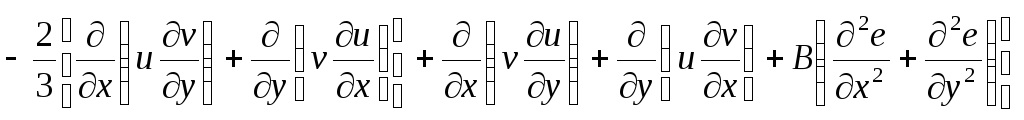(2.58)

В соответствии с рекомендациями разработчиков метода следует принимать = 0,01,B= 2,15.

.

Рис.2.4. Расчетная сетка, наложенная на обтекаемое тело, заштрихованы слои фиктивных ячеек

Записывая эту систему в конечных разностях с учетом обозначения С = t/sили, что то же самое, С = Сu/а, получим:

; (2.59)

; (2.60)

(2.61)

.

Параметры с дробными индексами, входящие в уравнения (2.59, 2.60) и относящиеся к границам ячеек, определяются как средние арифметические между значениями в примыкающих ячейках:

, . (2.62)

В некоторых формах записи уравнения (2.61) используются также значения

, . (2.63)

Далее следует второй, лагранжев этап, на котором определяются параметры переноса, соответствующие обмену между ячейками, когда происходит их перестройка в первоначальную эйлерову сетку. Необходимо найти потоки массы М за расчетный шагt, например, для правой границы:

, если 0 и (2.64)

, если 0.

На заключительном, третьем этапе шага по времени происходит перераспределение массы, импульса и энергии по пространству и определяются окончательные поля эйлеровых параметров потока на фиксированной сетке в момент времени tⁿ⁺¹=tⁿ+t. Соответствующие уравнения данного этапа являются выражениями законов сохранения массыM, импульсаPи энергииE, записанные для ячейки в разностной форме:

; (2.65)

; (2.66)

. (2.67)

Здесь соответственно М_гр,Р_гриЕ_гр– масса газа, импульс и величина полной энергии, связанная с этой массой, которые прошли за времяtодну из границ рассматриваемой ячейки. Очевидно, уравнения (2.65) – (2.67) записаны в предположении об отсутствии внутри ячейки источников массы, импульса и энергии.

Учитывая, что под действием перепада давлений на границах ячеек на первом этапе уже произошло изменение импульса, энергии, (масса не менялась), соответственно были получены значения промежуточных скоростей и энергии. Остается получить окончательные значения этих параметров в n+1 момент времени, уточненные за счет диффузионных процессов через границы ячеек:

; (2.68)

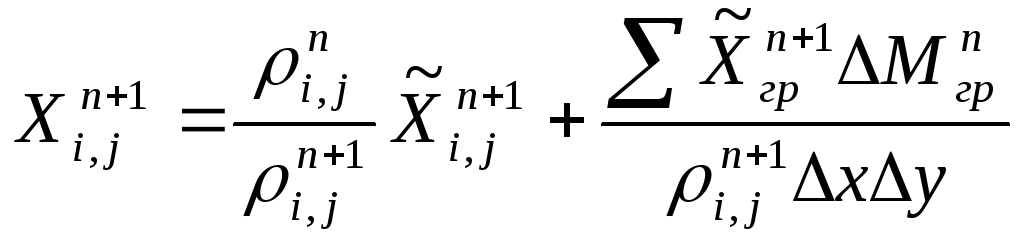, (2.69)

где Х = (u, v, E).

Таким образом, все параметры получены, и можно переходить к следующему временному слою.

Описанная расчетная схема соответствует базовому представлению МКЧ и является явной схемой первого порядка точности.